Este año, como todos los anteriores, algunas personas del ámbito de las matemáticas nos dedicamos a buscar propiedades matemáticas del número al que corresponde el nuevo año, en este caso, 2025, para incluir alguna de ellas en nuestras felicitaciones navideñas para compartir en las redes sociales, enviar a nuestros contactos por whatsapp o para diseñar nuestras tarjetas navideñas físicas. Por ejemplo, las pasadas navidades algunas personas compartimos que el número 2024, año en el que estamos y al que ya le faltan pocos días, es un número tetraédrico.

Los números tetraédricos son aquellos que son igual a la cantidad de naranjas que se necesitan para formar una pirámide de base triangular, es decir, un tetraedro. El 4 es un número tetraédrico, ya que podemos formar un tetraedro con tres naranjas abajo y una arriba, lo mismo ocurre con el 10, que es la cantidad de naranjas para una pirámide de tres alturas, con 6 naranjas abajo, 3 en medio y una naranja arriba. Y se necesitan 2.024 naranjas si realizamos una pirámide triangular de 22 alturas, con 253 naranjas abajo del todo. Por lo tanto, la cantidad de naranjas de las 22 filas son

1 + 3 + 6 + 10 + 15 + 21 + 28 + 36 + 45 + 55 + 66 + 78 + 91 + 105 + 120 + 136 + 153 + 171 + 190 + 210 + 231 + 253 = 2.024

En concreto, la pirámide triangular de 22 alturas es la que aparece en la siguiente imagen.

En particular, cada número tetraédrico, la cantidad de bolas de una cierta pirámide triangular, es igual a la suma de los primeros números triangulares (de los que vamos a hablar en breve), TT(n) = T(1) + T(2) + … + T(n), donde n es igual a la altura (en bolas) de la pirámide.

Suma de potencias

Pero vayamos con el número del nuevo año, el 2.025. Quizás la propiedad más impactante para utilizar como felicitación de año nuevo, para este 2.025, sea que puede escribirse como la suma de los cubos de todas las cifras básicas de nuestro sistema de numeración, es decir, todos los números de un solo dígito:

1³ + 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = 2.025,

donde no he incluido el cero ya que cero elevado al cubo es cero. Desde las navidades pasadas estoy esperando este momento, ya que el año pasado teníamos que 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ = 2.024, que también utilizamos bastante, pero nos faltaba el 1 para tener todos. Ahora ya podemos elegir una tipografía, un tamaño de letra, un fondo y un formato para la imagen … y esta podría ser mi tarjeta de año nuevo de este año.

Podemos continuar con las potencias con una propiedad muy sencilla, ya que 2.025 es un número cuadrado, es 45 al cuadrado,

45² = 2.025,

pero, además, puede escribirse como suma de cuadrados (de números no cero) de una sola manera, que es la siguiente

2.025 = 729 + 1296 = 27² + 36².

Números figurados (o geométricos)

Los números figurados son aquellos asociados a figuras geométricas, como el triángulo, el cuadrado o el tetraedro. Existen números figurados de distintas clases, bidimensionales como los poligonales, entre los que destacan los números triangulares, o los poligonales centrados; tridimensionales como los poliédricos, en especial los números tetraédricos; los números tetradimensionales, como los pentatópicos; o de otras dimensiones.

Un número poligonal es igual a la cantidad de puntos, o piedras, que se necesitan para representar una figura poligonal regular, como un triángulo equilátero (números triangulares), un cuadrado (números cuadrados), un pentágono (pentagonales), un hexágono (hexagonales) o cualquier otro polígono regular (véase el libro La gran familia de los números o la entrada El asesinato de Pitágoras, historia y matemáticas (y II)). Por ejemplo, los primeros números triangulares son 1, 3, 6, 10 y 15, ya que esta es la cantidad de piedras que se necesitan para formar un triángulo (de lado 1, 2, 3, 4 y 5 piedras), como se muestra en la siguiente imagen.

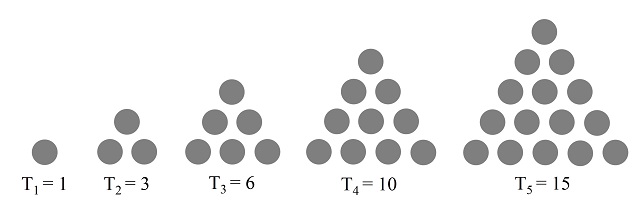
De la misma forma se construyen los primeros números cuadrados (1, 4, 9, 16 y 25), pentagonales (1, 5, 12 y 22) o hexagonales (1, 6, 15 y 28).

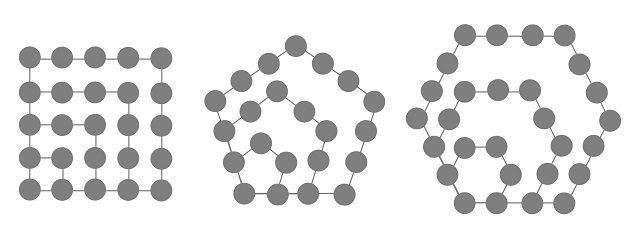
El número 2.025 no es un número triangular, pero puede escribirse como suma de números triangulares consecutivos, en concreto,

2.025 = 990 + 1.035 = T(44) + T(45).

Más aún, el número del próximo año puede expresarse como resta de números triangulares, por ejemplo, 2.025 = T(407) – T(402), lo que hace que pueda escribirse, si tenemos en cuenta que el número triangular n-ésimo T(n) es la suma de los primeros números hasta n, es decir, T(n) = 1 + 2 + 3 + … + n, como suma de números naturales consecutivos

2.025 = 403 + 404 + 405 + 406 + 407,

lo que hace que el 2.025 pertenezca a la familia de los números corteses, o trapezoidales.

Más aún, el 2.025 se puede expresar como suma de números naturales consecutivos no solo como se ha mostrado arriba, sino de catorce formas distintas, como se indica en la siguiente imagen.

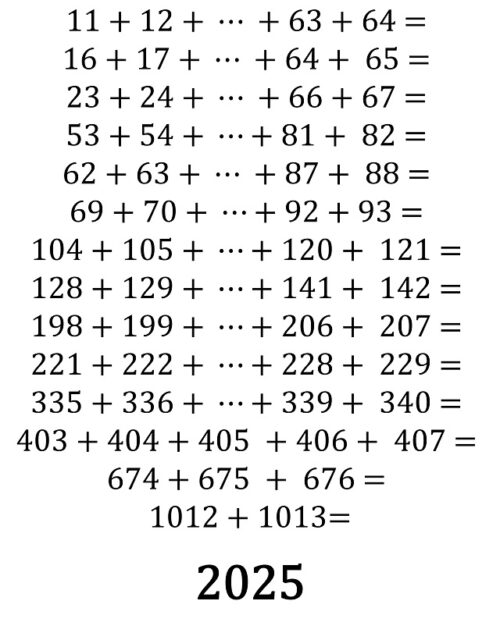
Como ya hemos comentado antes, el número 2.025 es un número cuadrado, ya que es igual a la cantidad de piedras que se necesitan para formar un cuadrado de 45 piedras de lado, 2.025 = 45².

Pero aún tenemos otra propiedad del 2.025 relacionada con los números figurados, pero esta vez con los números poligonales centrados. Esta es otra familia de números figurados que son también la cantidad de puntos que se necesitan para representar una figura poligonal regular, pero con una configuración distinta a la anterior, con un punto en el centro y los puntos con la forma del polígono alrededor.

Como se muestra en la siguiente imagen, los primeros números triangulares centrados son 1, 4, 10 y 19; los primeros cuadrados centrados son 1, 5, 13 y 25; los pentagonales centrados 1, 6, 16 y 31; y los hexagonales centrados (llamados números hex por el divulgador de las matemáticas estadounidense Martin Gardner (1914-2010)) 1, 7, 19 y 37.

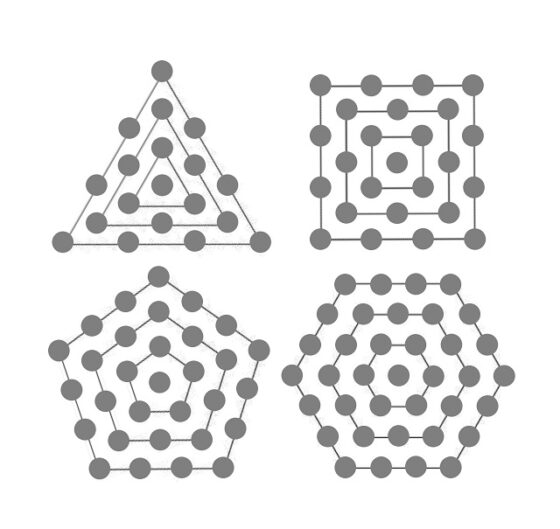
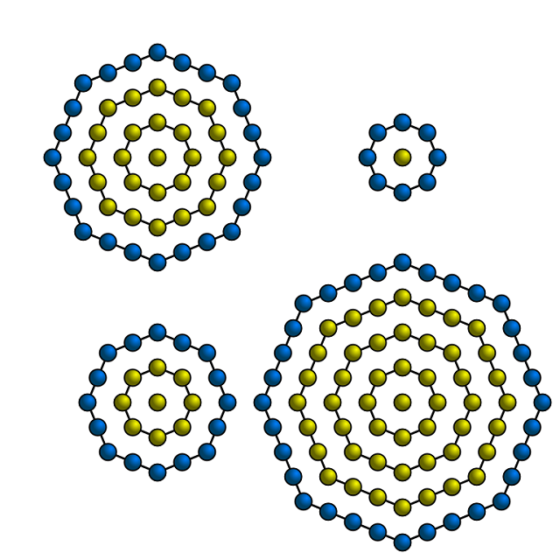
Resulta que nuestro número, 2.025, es un número octogonal centrado. Los primeros de esta familia son 1, 9, 25 y 49, como se muestra en la siguiente imagen. El número 2.025 es el vigésimo tercer número octogonal centrado, es decir, se obtiene como acumulación de 23 octógonos alrededor de un punto, incluido este.

Los divisores tienen la palabra

A continuación, vamos a hablar de propiedades relacionadas con los divisores de los números, en concreto, del número 2.025. La descomposición factorial de este número es la siguiente

2.025 = 3⁴ x 5².

Por lo tanto, nuestro número tiene quince divisores, que son 1, 3, 5, 9, 15, 25, 27, 45, 75, 81, 135, 225, 405, 675, 2.025. En particular, 2.025 no es un número primo, luego es un número compuesto.

En la entrada del Cuaderno de Cultura Científica titulada Los números enamorados se hablaba de familias de números, como los números amigos, sociables, novios, perfectos, abundantes, deficientes, casi-perfectos, multiperfectos, ambiciosos, raros o poderosos, todas ellas relacionadas con la suma de los divisores de un número. La suma de los divisores propios (sin incluir el número) del 2.025 es 1.726, por lo que no es un número perfecto, puesto que la suma debería ser nuestro número, pero como es menor que el mismo, es lo que se denomina un número deficiente.

Por otra parte, existe una familia de números, que se conoce con el nombre de números tau, que son aquellos que son divisibles por la cantidad de divisores. Como 15, que es el número de divisores de 2.025, divide a este, resulta que el nuevo año es un número tau.

Además, 2.025 es un número duffiniano (nombre dado en honor al matemático estadounidense L. Richard Duffy, que fue quien introdujo este concepto), ya que no tiene factores comunes con la suma de sus divisores (incluido el propio número), 3.751, cuya descomposición factorial es 11² x 31.

Por sus dígitos los conoceréis

Existen varias propiedades relacionadas con los dígitos de un número, como las que satisfacen los números narcisistas, potentes o de Munchausen, de los que hablamos en la entrada ¿Pueden los números enamorarse de su propia imagen?, o los números de Harshad, también llamados de Niven, a los que dedicamos la entrada Los números que proporcionan alegría. El número al que estamos dedicando esta entrada, el número del próximo año, no cumple muchas de estas propiedades, pero sí alguna.

El 2.025 es un número de Harshad ya que la suma de sus dígitos, 9, divide al número. Además, como el 2.025 es divisible por el número formado por el primer y el último dígito, 25, se dice que es un número “gapful” (que quizás podríamos traducir como “número con laguna”).

Un número que quería ser capicúa

Vamos a terminar con una sencilla cuestión relacionada con los números capicúas. Como todo el mundo sabe, un número es capicúa, o palíndromo, si sus dígitos leídos de izquierda a derecha y de derecha a izquierda son los mismos. Es muy fácil construir, o identificar, capicúas. Por ejemplo, 12.733.721 es un número capicúa, pero 2.025, claramente, no lo es.

Entonces, si el número al que estamos dedicando esta entrada no es capicúa, nos podemos preguntar por qué estamos hablando de esta cuestión. Como explicamos en la entrada El secreto de los números que no querían ser simétricos, existe una curiosa forma de obtener números capicúas a partir de cualquier número, bueno casi cualquiera, el algoritmo “invierte el orden y suma”. Consideremos un número cualquiera, por ejemplo, el 75, entonces le sumamos su simétrico, el 57, de donde se obtiene 75 + 57 = 132, que no es palíndromo, pero volvamos a realizar el mismo proceso con este resultado, 132 + 231 = 363, que ahora sí es capicúa, y lo hemos conseguido en dos pasos.

Para cada número se necesitan una cantidad distinta de pasos para llegar al número capicúa. Por ejemplo, si tomamos como punto de partida el número 89, se necesitan 24 pasos hasta llegar al capicúa 8.813.200.023.188, como podéis comprobar vosotros mismos. Pero, a día de hoy, no se sabe si esto ocurre para absolutamente todos los números, como podéis leer en la entrada anteriormente citada o en el libro La gran familia de los números.

Aunque para el número 2.025 sí ocurre y además en un solo paso, ya que

2.025 + 5.202 = 7.227,

que es capicúa.

Estas son algunas de las propiedades del número 2.025, aunque hay muchas más, pero no hablaremos de ellas en esta entrada.

Y, para terminar, simplemente desearos a todas las personas que estáis leyendo esto …

¡Feliz año 2.025!

Bibliografía

1.- Ibáñez, La gran familia de los números, Libros de la Catarata, 2021.

2.- Página web: Numbers Aplenty.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica