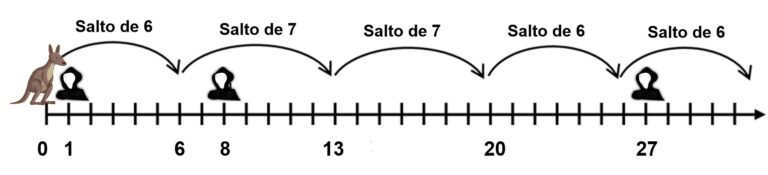
Al rescate dando saltos
Hoy planteamos un pequeño problema matemático relacionado con teoría de congruencias.
El problema de la madre canguro
Un bebé canguro ha sido secuestrado por el malvado matemático Moriarti. Mientras gestiona su venta al mejor postor, el villano ha dejado al animalito colocado en el número 2100 de una línea numérica.
La madre canguro está situada en la posición 0 de esa recta numérica e intentará rescatar a su hijo. Es capaz, y es lo que hace normalmente, de dar saltos de 6 unidades.
Pero Moriarti no se lo va a poner fácil. El perverso matemático tiene guardas situados en las posiciones n3 de la recta numérica, para cada número entero positivo n. Si la canguro cae en un número ocupado por un guarda, será atrapada y su misión fracasará: Moriarti se quedará con el bebé canguro y lo venderá. En caso contrario, la madre se zafará del guarda y continuará saltando para intentar alcanzar a su hijo.
Además, cada vez que consigue eludir a un guarda, la mamá canguro siente una descarga de adrenalina que hace que su siguiente salto (solo el primero tras evitar a un guarda) sea de 7 unidades en lugar de 6. Tras ese único salto de 7 unidades, la canguro vuelve a saltar 6 unidades en cada brinco, hasta el siguiente momento que consiga escabullirse de un guarda (si es que esta situación es posible).
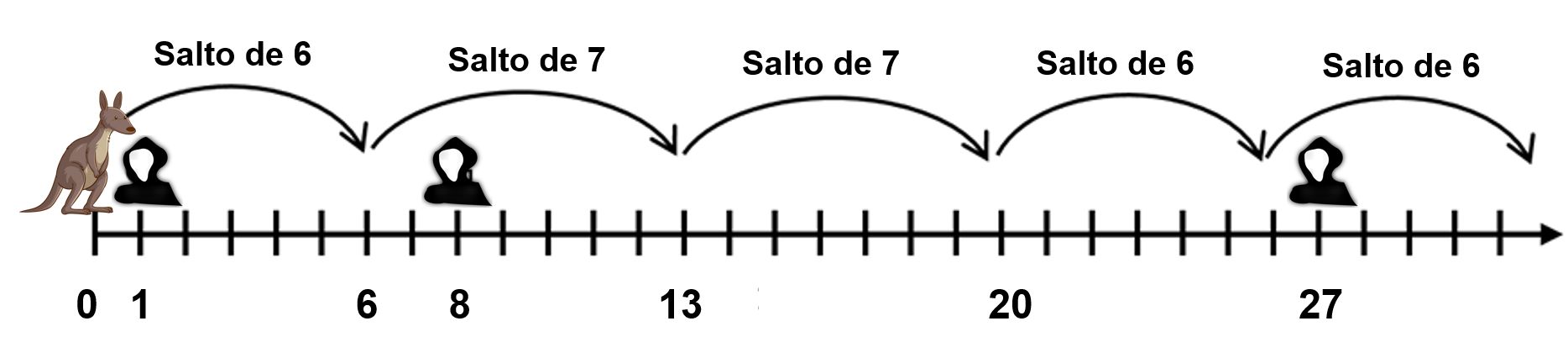
La pregunta que planteamos es la siguiente:
¿Podrá la mamá canguro alcanzar (o pasar) a su hijo sin ser atrapada?
La solución
Observemos en primer lugar que la diferencia entre los cubos de dos números enteros consecutivos es siempre un múltiplo de 6 desplazado en una unidad. En efecto, si desarrollamos:
(n+1)3 = n3 + 3n2 + 3n + 1.
Se deduce inmediatamente que
(n+1)3 – n3 = 3n2 + 3n + 1 = 3n(n+1) + 1.
El producto n(n+1) es necesariamente par (si n no es par, lo es n+1), así que 3n(n+1) es múltiplo de 6. En términos de congruencias, diríamos que (n+1)3 – n3 es congruente con 1 módulo 6 (dicho de otro modo, si dividiéramos (n+1)3 – n3 entre 6, el resto de la división sería 1).
En segundo lugar, observemos como son los primeros saltos de la mamá canguro: salta de 0 a 6 (ha salvado al guarda situado en la posición 13 = 1, así que el siguiente salto es de 7 unidades), de 6 a 13 (ha salvado el guarda colocado en 23 = 8, así que el siguiente salto es de 7 unidades), de 13 a 20, de 20 a 26, de 26 a 32 (ha salvado el guarda colocado en 33 = 27, así que el siguiente salto es de 7 unidades), etcétera.
Pero no podemos seguir argumentando de este modo porque, aunque los cubos de los enteros positivos crecen deprisa (1, 8, 27, 64, 125, 216, 343, 512, 729, 1000…), el número 2100 es enorme (luego volveremos a ello).
Antes de continuar, observemos que el segundo y el tercer saltos son los únicos consecutivos de 7 unidades (23 – 13 = 7; como la canguro sobrepasa con su salto al 1, con su siguiente salto de 7 unidades, sobrepasa al 8). En efecto, para n > 1 (n mayor o igual a 2), la diferencia (n+1)3 – n3 = 3n(n+1) + 1 es mayor o igual a 19. Así, para n > 1, si la canguro sobrepasa n3, con un salto de 7 unidades no puede alcanzar la posición (n+1)3.
Ahora, nuestra estrategia consistirá en razonar por reducción al absurdo; supongamos que la canguro es atrapada por el guarda situado en el lugar (n+1)3. Eso significa que ha pasado por encima del guarda colocado en n3 y, por lo tanto, ha dado un (único) salto de 7 y varios saltos de 6 hasta caer en la posición (n+1)3. Es decir, tras sobrepasar al guarda en la casilla n3, ha saltado 7 + 6k números, donde k es algún entero positivo. Pero hemos demostrado anteriormente que la distancia entre dos guardas (la cantidad (n+1)3 – n3) es un número congruente con 1 módulo 6. Así que, si la canguro ha caído en el número (n+1)3, contando hacia atrás, ¡ha tenido que caer también en la posición del guarda anterior, el colocado en la posición n3! Pero esto es imposible, ya que es el guarda situado en el lugar (n+1)3 el (primero) que apresa a la madre canguro.
De aquí se deduce que la canguro nunca será detenida y, salto a salto, conseguirá alcanzar (o sobrepasar a su hijo) y de este modo rescatarlo.
Pero… ¿es tan grande el número 2100?
2100 es el siguiente número de 31 dígitos:
1 267 650 600 228 229 401 496 703 205 376.
En notación decimal, es 1,267650600228229401496703205376 x 1030.
Y sí, es un número realmente grande; recordemos, por ejemplo, que se estima que el universo posee 1025 estrellas…
Por cierto, una forma de calcular este número es observando que 210 = 1024. Y entonces 2100 = (210)10 = (1024)10… ¡Y ya solo quedarían por hacer diez multiplicaciones!
Referencia
- Jumping Kangaroos, Futility Closet, 18 de julio de 2025
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia