Un tema con cierta popularidad dentro de la cultura matemática son los denominados “grandes números”. Normalmente, bajo la nomenclatura de “grandes números” se incluyen números más grandes de lo que es habitual utilizar en la vida cotidiana, en el día a día. La verdad es que es un concepto un poco ambiguo, pero tampoco hace falta que seamos muy estrictos con la definición para realizar un pequeño paseo sobre el tema.
La Enciclopedia Británica dice que hablamos de grandes números cuando son cantidades mayores que un millón, y que de manera normal suelen escribirse en forma de potencia. Un clásico, que además es fuente de muchos errores, es el billón, que en la notación de exponentes sería 1012, es decir, un 1 seguido de 12 ceros (1.000.000.000.000). Un millón de millones. La confusión relacionada con el billón está en el hecho de que en inglés (*) un “billón” son “mil millones”, es decir, 109 (1.000.000.000). Por este motivo, en ocasiones se dan noticias que son traducciones de noticias de países de habla inglesa y se utiliza, incorrectamente, el billón, cuando debería utilizarse el millardo, que es nuestra palabra para los mil millones.
Por ejemplo, en el libro Disparates y gazapos matemáticos, de Jose María Sorando, publicado por la editorial Catarata, se cita el siguiente ejemplo. En cierta ocasión en La Sexta Noticias se decía lo siguiente:
“[Madonna] Está considerada la artista más rica de la historia de la música. La reina del pop tiene una fortuna estimada entre 800 millones y un billón de euros. ¡Sí, con b!”.
La noticia quería transmitir la idea de que la artista tenía entre 800 y 1.000 millones de euros, pero la horquilla se les disparó al utilizar el término billón, que aparecía en la noticia en inglés, ya que expresaba que la artista tenía entre 800 y un millón de millones de euros.

Aprovechando que hablamos de millardos (109) y billones (1012), que son dos números que todos conocemos, podemos realizar un pequeño experimento que nos permita reflexionar sobre hasta qué punto somos conscientes del valor de los grandes números. Este experimento lo leí hace años en el libro El universo y la taza de té, de la divulgadora científica K. C. Cole.
Para empezar, recordemos que en matemáticas se suelen representar los números en una línea, que puede ser abierta o cerrada. En este último caso, se coloca el número más pequeño que se quiere representar (por ejemplo, el cero) a la izquierda, mientras que el número más grande se representa a la derecha y el segmento entre ambos extremos (números) se divide de forma que se representen linealmente todos los números entre esos dos números extremos. Por ejemplo, si tomamos el segmento con extremos 0 y 10, como en la siguiente imagen, tendremos los números 1, 2, 3, 4, 5, 6, 7, 8 y 9 entre ellos, igualmente espaciados.
Hay que tener en cuenta que en la recta de los números no solo se representan los números naturales, sino todos los números reales entre 0 y 10, aunque esta cuestión no es algo importante para nuestro experimento de esta entrada.
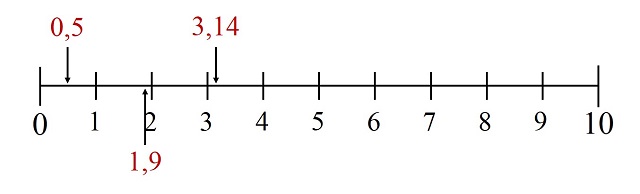
Pero vayamos con el experimento. Tomamos una hoja de papel y la colocamos en horizontal. Esto es para que tengamos más longitud para pintar una línea horizontal y esto precisamente lo que hacemos a continuación, pintar un segmento que vaya de un extremo a otro de nuestra hoja. De manera que en el extremo izquierdo colocamos el cero (0) y en el extremo derecho el billón (1012), como aparece en la imagen.

El experimento consiste en que marquéis con un segmento vertical el lugar en el que estará representado, en la línea de los números, el millardo (109). La idea es que realicéis esta primera parte del experimento de forma intuitiva, sin pensar mucho en ello. Os animo a que antes de seguir leyendo realicéis esta primera parte, para poder reflexionar sobre el resultado.
Entonces, viene la segunda parte del experimento, que consiste en reflexionar con tranquilidad dónde estará situada la marca del millardo en la línea de los números. Para ello vamos a dividir nuestro segmento en diez partes iguales, cada una de las cuales se va a corresponder con la décima parte del billón que representa la recta, luego 100.000.000.000 (cien mil millones). Por lo tanto, las marcas entre cero (0) y un billón (1012), igualmente espaciadas, serán las posiciones de los números 100.000.000.000, 200.000.000.000, 300.000.000.000, …, 900.000.000.000, como se ve en la imagen.

Ahora, dividiremos la parte del segmento entre 0 y 100.000.000.000 (que es la primera marca de la izquierda después del cero), en diez partes iguales, cada una de las cuales se va a corresponder con la décima parte de 100.000.000.000 que representa ese trozo de segmento, luego 10.000.000.000 (diez mil millones). Por lo tanto, las marcas ahora entre cero (0) y cien mil millones (100.000.000.000), igualmente espaciadas, serán las posiciones de los números 10.000.000.000, 20.000.000.000, 30.000.000.000, …, 90.000.000.000.
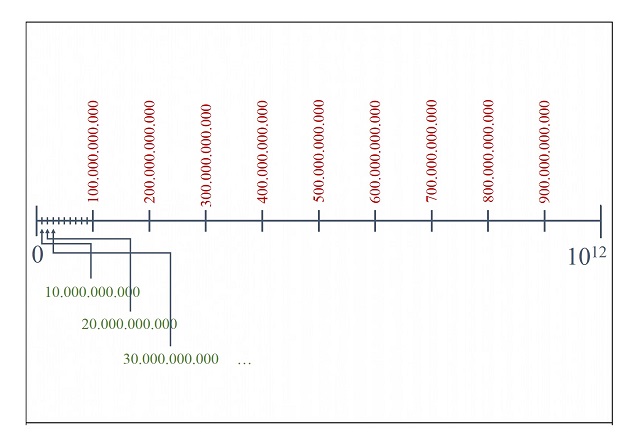
Pero nosotros estamos buscando representar el millardo (1.000.000.000), que es más pequeño aún que el número de la primera marca, que es 10.000.000.000. Por lo tanto, por último, tendríamos que dividir la parte del segmento entre 0 y 10.000.000.000 (que es esa primera marca de la izquierda después del cero, que acabamos de introducir), en diez partes iguales, cada una de las cuales se va a corresponder con la décima parte de 10.000.000.000 que representa ese trozo de segmento, luego 1.000.000.000 (mil millones). Ahora, como antes, pintaríamos las marcas entre cero (0) y diez mil millones (10.000.000.000), igualmente espaciadas, y la primera de ellas sería la que se corresponde con el número 1.000.000.000 (mil millones, el millardo), que es el que estábamos buscando representar. Aunque esta última parte no la hemos representado, ya que no tenemos espacio para las marcas, resulta evidente que el millardo, que sería la primera de esas marcas, está al lado del cero, pegadito al 0. Es decir, un millardo (mil millones) es prácticamente cero comparado con el billón (un millón de millones).
¿Dónde lo habíais colocado inicialmente? Es muy típico que, si no pensamos mucho en ello, lo coloquemos de la mitad del segmento inicial hacia la derecha, muy lejos de donde realmente está. Eso es porque pensamos más en el exponente, 9 frente a 12 (la cantidad de ceros) de su representación, que en el valor del número.

Volviendo a los grandes números, la verdad es que podemos sacar ejemplos de ellos, no solo en matemáticas, como haremos más adelante, sino en otros ámbitos de la vida y la cultura.
Por ejemplo, la cantidad de plaquetas de nuestro cuerpo es aproximadamente 1,8 billones, es decir, 1,8 x 1012 (resulta que el cuerpo humano tiene entre 4,5 y 6 litros de sangre, que hay 300.000 plaquetas por milímetro cúbico y que cada litro contiene 1.000.000, un millón, de milímetros cúbicos, luego de ahí nos sale que hay del orden de 1,8 billones de plaquetas en nuestro cuerpo). Pero podríamos seguir. La cantidad de células en el cuerpo humano es de 37 billones, es decir, 37 x 1012, la cantidad de configuraciones del cubo de Rubik es, aproximadamente, de 43 trillones, es decir, 43 x 1018 o el número de estrellas en el universo (observable) se estima que es alrededor de un cuatrillón, es decir, 1024.

Pero también podemos mirar a la literatura. Uno de los poemas más famosos del poeta francés Paul Fort (1872-1960) es Un corro alrededor del mundo (1913), que es un llamamiento a la amistad mundial y que dice así:
Si todas las muchachas del mundo quisieran darse la mano,
podrían hacer un corro todo alrededor del mar.
Si todos los muchachos del mundo quisieran ser marineros,
harían con sus barcas un hermoso puente sobre las olas.
Se podría hacer un corro alrededor del mundo,
si toda la gente del mundo quisiera darse la mano.
Quedémonos con esta última parte “si toda la gente del mundo quisiera darse la mano se podría hacer un corro que diese la vuelta al mundo”. Aunque la población mundial hoy en día es muy superior, en la época en la que se escribió este poema había unos dos mil millones de habitantes (2.000.000.000) y el perímetro de la Tierra es, alrededor del ecuador, de 40.075 kilómetros. Por lo tanto, si todas las personas de nuestro planeta, en aquel momento, se hubiesen dado la mano, y asumiendo que cada una de las personas representa un eslabón de 1 metro, que estirados sería aún más, tendríamos una cadena de personas de 2 mil millones de metros, luego que podría rodear casi 50 veces la Tierra.
Teniendo en cuenta que en la actualidad la población mundial es de 8 mil millones de personas, podríamos formar un corro que diese la vuelta a la Tierra, por el ecuador, 200 veces.
Si miramos al mundo del arte también tenemos algunos ejemplos curiosos. Recientemente, he estado estudiando la obra de un artista abstracto eslovaco, Viktor Hulik (1949), por su relación con algunas cuestiones matemáticas, en concreto, obras como Variaciones con triángulos (2014) están creadas con sencillas estructuras cuadradas divididas en dos triángulos por la diagonal, lo que se conoce como la baldosa de Truchet (podéis leer sobre ella en las entradas del Cuaderno de Cultura Científica: Los embaldosados de Truchet y el puzle del diamante y El arte de la sencilla baldosa de Truchet).
Pero volviendo a esta obra de Viktor Hulik, está compuesta de 12 lienzos cuadrados, que en cada exposición coloca de forma aleatoria, formando una estructura rectangular 3 x 4. Por una parte, cada uno de los 12 lienzos es una estructura reticular cuadrada 8 x 8, formada por 64 baldosas de Truchet de alguno de los tres pares de colores siguientes, blanco y gris; blanco y negro; gris y negro. Por lo tanto, existen (4 + 4 + 4)64 = 1264 estructuras posibles (más de mil ciento sesenta y ocho undecillones) para esos lienzos.
Por otro lado, como en cada exposición el artista eslovaco coloca de forma distinta esos 12 lienzos formando una estructura 3 x 4, en cada exposición se ve, realmente, una obra distinta. La cuestión es que podemos calcular matemáticamente de cuántas formas distintas se pueden colocar los 12 lienzos de la obra de Viktor Hulik, en concreto, son (412) x (12!) = 8.036.313.307.545.600, más de 8 mil billones, de formas distintas de colocarlos. Si cada minuto se realizase una nueva disposición, y distinta a las anteriores, de los 12 lienzos de la obra Variaciones con triángulos, se tardarían 15 mil millones de años en mostrar todas las estructuras posibles de esa obra, lo que es más que la edad del universo, ya que según la cosmología la edad del universo, desde el Big Bang, sería de unos 13.787 millones de años.

Pero, si nos adentramos en los grandes números en matemáticas, el más famoso de todos es sin lugar a dudas, el googol. De hecho, en matemáticas es relativamente normal inventarnos nombres y notaciones para números grandes. Así lo hicieron los matemáticos estadounidenses Edward Kasner y James R. Newman en su libro Matemáticas e Imaginación (1940), que se inventaron el número “googol”, al que le dieron el valor de 10100 (un 1 seguido de 100 ceros), es decir, diez mil hexadecillones.
10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000
Según se cuenta el nombre “googol” fue inventado por el sobrino de 9 años de Edward Kasner. En concreto, en el libro Matemáticas e Imaginación está escrito lo siguiente.
Palabras de sabiduría pronuncian los niños, por lo menos tan a menudo como los hombres de ciencia. El nombre “googol” fue inventado por un niño (sobrino del doctor Kasner, de nueve años de edad), a quien se le pidió que propusiera un nombre para un número muy grande, a saber: un 1 seguido de cien ceros. Estaba muy seguro de que este número no era infinito y, por lo tanto, igualmente en lo cierto de que debía tener un nombre. Al mismo tiempo que indicó la palabra “googol”, sugirió el nombre de otro número aún mayor: “googolplex”. El googolplex es mucho mayor que el googol, pero continúa siendo finito, como se apresuró a señalar el inventor de su nombre. Primero se sugirió que un googolplex sería un 1 seguido por tantos ceros que uno se cansase de escribirlos. Esto es una descripción de lo que sucedería si uno tratara realmente de escribir un googolplex, pero distintas personas se cansan en tiempos diferentes […].
A continuación, como la definición de googolplex como “un 1 seguido por tantos ceros que uno se cansase de escribirlos” no era muy rigurosa, ya que “pero distintas personas se cansan en tiempos diferentes”, entonces se definió el googolplex como 10 elevado a un googol:
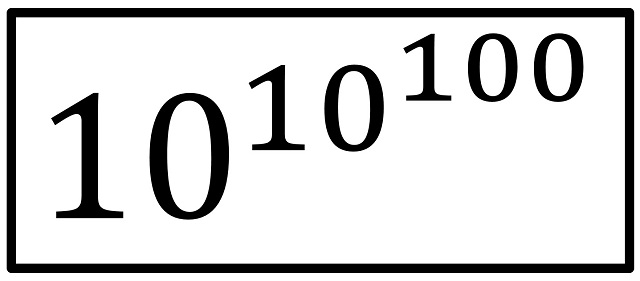
Es decir, un 1 seguido de un googol de ceros.
Pero, volviendo a la primera definición “un 1 seguido por tantos ceros que uno se cansase de escribirlos”, que ha sido sustituida por “un 1 seguido de un googol de ceros”, la verdad es que hemos pegado un salto cualitativo ya que no disponemos de tiempo para escribir un googol de ceros, ni siquiera aunque viviéramos tanto como la edad de nuestro universo. Supongamos que cada segundo escribimos tres ceros, que escribimos a ese ritmo de forma incansable, sin parar, toda la edad de nuestro universo, que son 13.787 millones de años, entonces escribiríamos tan solo
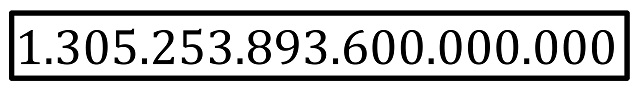
ceros. Y nos quedamos lejos del googol, ya que esa cantidad es del orden de 10 elevado a 18, es decir, un 1 seguido de 18 ceros, lejos de los 100 del googol.
Por otra parte, aunque parezca mentira estos números, el googol y el googolplex, han gozado de una cierta popularidad. Por ejemplo, el googol apareció en una de las tiras de humor de Snoopy, que vemos en la siguiente imagen. En ella puede verse a los personajes de Schroeder y Lucy juntos, entonces esta le pregunta a su amigo “Schroeder, ¿cuál crees que es la probabilidad de que me case algún día?” y su amigo le contesta “yo diría que una entre un googol”, y Lucy le pregunta qué es un googol y la respuesta de Schroeder en la viñeta es literalmente un uno seguido de 100 ceros, lo cual llena media viñeta, y Lucy se queda con cara de circunstancias).

Mientras que el googolplex ha aparecido en series como Los Simpson, donde hay un cine que se llama Googolplex, o en la serie de dibujos Phineas y Ferb, donde hay un centro comercial con ese mismo nombre.

Por otra parte, el nombre del buscador más famoso de internet Google, le debe su nombre a este número, al googol. La historia es la siguiente, según puede leerse en la página de David Koller, de la Universidad de Standford (California), donde se creó google.
En 1996, los estudiantes de doctorado de la Universidad de Stanford Larry Page and Sergey Brin inventaron un magnífico buscador que inicialmente bautizaron con el nombre de «BackRub», nombre que estaba relacionado con el proceso que realizaba el buscador, pero que no era muy atractivo, ni comercial. Y empezaron a buscar un nuevo nombre para el buscador, que fuera más apropiado. En una sesión de “lluvia de ideas” de Larry Page, junto con otros estudiantes de doctorado, entre ellos Sean Anderson, este propuso verbalmente el nombre de «googolplex» y Larry contestó que mejor «googol». Entonces, Sean se sentó en un ordenador a buscar si el dominio de internet de “googol” estaba libre, pero lo escribió mal, escribió “google.com”, en lugar de “googol.com” (en inglés ambas palabras se pronuncian de forma parecida, algo así como “gúgol”). Resultó que “google.com” estaba libre y a Larry Page le gustó el nombre y lo registró.

Pero eso de inventarnos números grandes no es algo moderno. Por ejemplo, en la Antigua India tenían diferentes palabras para números grandes. Por ejemplo, Asankhyeya, que significa literalmente «incontable» en sánscrito, es un número que equivale a 10140 (1 seguido de 140 ceros). Asankhyeya es una palabra que aparecía a menudo en los textos budistas y que venía a significar una cantidad infinita.
Aunque un número realmente gigante, volviendo a las matemáticas, es el número de Skewes, que es “diez elevado a diez elevado a diez elevado a 34”,
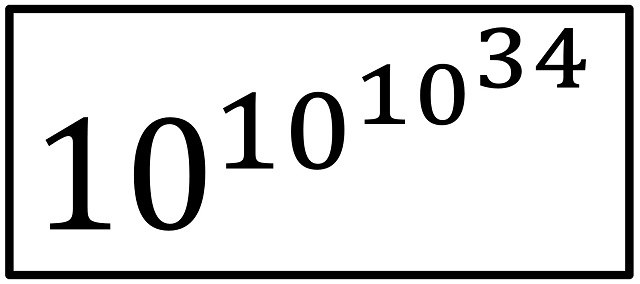
que durante un tiempo fue el número más grande que aparecía en una demostración matemática (en concreto, en un artículo del año 1933). Este número está relacionado con la distribución de los números primos, con la conocida Hipótesis de Riemann, pero ese es otro tema.
La verdad es que hemos pegado un salto muy grande. Volvamos un poco para atrás. Podríamos preguntarnos cuál es el número más grande que se puede formar con tres cifras, sin utilizar otros signos matemáticos. En un principio podríamos pensar que quizás fuese 999, pero resulta que no es así. El número más grande que se puede formar con tres cifras es
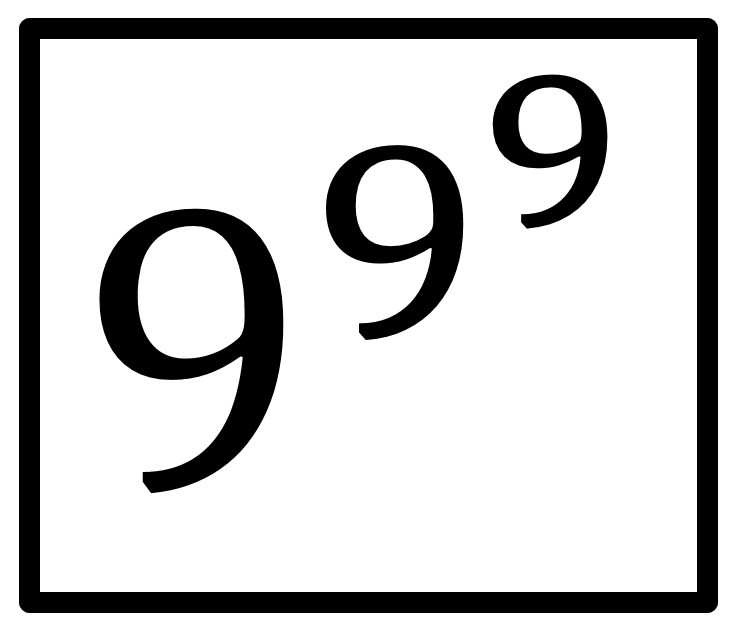
es decir, nueve elevado a nueve elevado a nueve. A este número le ocurre como a muchos otros grandes números, que a pesar de la sencillez con la que los expresamos, sin embargo, es difícil calcularlo y tener información sobre el mismo. Por ejemplo, ¿cómo de grande es este número (nueve elevado a nueve elevado a nueve)? Podríamos empezar por calcular 9 elevado a 9, que es 387.420.489, luego nuestro número es 9 elevado a este número, y esto no es sencillo de calcular. En 1906 se demostró que este, aparentemente sencillo número, tiene 369.693.100 dígitos (¡más de 369 millones de dígitos!).
Para hacernos una idea del orden de magnitud de este número (que es mayor que el googol, pero mucho más pequeño que el googolplex), imaginemos que lo queremos escribir, y lo vamos a hacer dedicando, de media, un segundo por cada cifra escrita y turnándonos varios amigos en la tarea para no parar de escribir en ningún momento. Tardaríamos entonces 11 años, 263 días, 20 horas, 31 minutos y 40 segundos en escribir el número “9 elevado a 9 elevado a 9”.
Pero, además, ¿cuánto espacio necesitaríamos para escribirlo? Si tomamos una hoja de papel, podemos escribir en una página 2.100 caracteres –30 líneas de 70 espacios cada línea-, entonces se precisarían 176.045 páginas de papel (la última solamente escrita hasta la tercera parte). Si, una vez escritas todas estas hojas de papel (que están escritas por una sola cara), queremos almacenarlas, ¿cuánto espacio nos ocuparán físicamente estos papeles sobre los que hemos escrito el número “9 elevado a 9 elevado a 9”? Cada hoja de papel tiene, más o menos, un grosor de 0,1 mm por hoja, luego 1000 hojas tienen un grosor de 100 mm, luego la cantidad de hojas escritas con el mencionado número ocuparán más de 18 metros de altura.

Volviendo a números grandes que aparecen en demostraciones matemáticas, como el número de Skewes (10 elevado a 10 elevado a 10 elevado a 34), en el libro Guinness de los Records de 1980 aparece el número de Graham como el “número más grande que aparece en una demostración matemática”, frase que escribió el divulgador Martin Gardner en su columna de Juegos Matemáticos de Scientific American en 1977. Pero su definición es lo suficientemente compleja para que lo dejemos para otra ocasión.
Bibliografía:
1.- K. C. Cole, El universo y la taza de té. Las matemáticas de la verdad y la belleza, Ediciones B, 1999.
2.- André Jouette, El secreto de los libros, Ma non tropo, 2000.
3.- Edward Kasner, James R. Newman, Matemáticas e imaginación, Salvat, 1986.
4.- Clifford A. Pickover, El prodigio de los números, Ma non troppo, 2002.
5.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, Catarata, 2023 (pendiente de publicación).
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
(*) Nota del editor:
En puridad el valor otorgado a los términos billón, trillón u otros depende de que en una comunidad de hablantes se empleen las escalas numéricas corta o larga. Esta asignación ha variado a lo largo de la historia y no es homogénea en el mundo. En general, en los países colonizados por Inglaterra se emplea la escala corta pero no es algo exacto. Así, es probable que un canadiense francófono use la escala larga, mientras que uno anglófono use la corta. Una persona británica, una ucraina o una brasileña usarán la corta, pero una portuguesa, una española o una argentina usarán la larga. Sobre todo esto véase: Long and short scales. Por simplificar, y por ser cierto en sentido estricto, matenemos el texto original de Raúl.
Un pequeño paseo por los grandes n&uacut…
[…] Los denominados “grandes números” incluyen números más grandes de lo que es habitual utilizar en la vida cotidiana, en el día a día […]