Las personas que tenemos cierta edad recordamos haber visto las películas, series y grabaciones caseras en cintas de video VHS o Beta, al ser reproducidas en sus correspondientes aparatos de video, mucho antes que los DVD, los discos de Blu-ray (alta definición) o las plataformas digitales actuales a través de internet.

Los sistemas de video VHS (Video Home System), de la compañía japonesa JVC (Japan Victor Company), Beta (Betamax), de la empresa multinacional, con sede en Japón, Sony, y Video2000, de la compañía neerlandesa Phillips, fueron desarrollados en la década de 1970. Entre ellas se produjo una guerra comercial por quedarse con el mercado de las cintas de video, en la cual el sistema Video2000 quedó rápidamente fuera de combate y se impondría el sistema VHS, a pesar de que, según los expertos, el sistema Beta era mejor.

Para entender por qué el sistema de video VHS se impuso al sistema Beta, vamos a empezar por comparar las características generales de ambos sistemas. Ambos sistemas se comercializaron prácticamente a la vez, en 1975 el sistema Betamax y un año después VHS. El sistema Beta era superior en calidad de imagen a VHS y sus casetes eran más pequeños y compactos, luego más manejables. Por el contrario, el sistema VHS tenía una duración mayor de grabación (en un principio 2 horas, frente a una hora de Beta) y tenía una licencia abierta, permitiendo a otros fabricantes, como Panasonic, Hitachi, Mitsubishi o TDK, producir equipos de video VHS y casetes. Son precisamente estas características de VHS las que hicieron, según los expertos, que este sistema se impusiera al que a priori era superior en calidad de imagen, que la grabación fuese inicialmente de dos horas, lo que permitía grabar una película entera en una única cinta, y tuviese licencia abierta, lo que convertía a otras empresas en sus aliadas comerciales.

Guerras comerciales

Al igual que nos hemos planteado la pregunta ¿por qué el sistema de video VHS desbancó al sistema Beta, que según algunos expertos era un sistema mucho mejor?, también podemos cuestionarnos ¿por qué se impuso el sistema de teclados QWERTY en las máquinas de escribir y en los ordenadores (fíjate en la primera línea de letras, arriba a la izquierda, de tu ordenador) sobre otros sistemas, como el DSK, algunos de los cuales eran mejores sistemas que permitían escribir más rápido? ¿por qué en la conocida guerra de las consolas entre las empresas Sega y Nintendo se impuso esta última? ¿por qué la bebida carbonatada Coca Cola se impuso a su rival Pepsi? Y podríamos continuar con otras guerras comerciales, las hamburgueserías Burger King y McDonalds, las empresas Apple y Microsoft, las consolas PlayStation y Xbox, las enciclopedias digitales Wikipedia y Encarta, las redes sociales Facebook y Twitter, entre muchos otros posibles ejemplos.

Al estudiar o discutir situaciones como las comentadas, las personas expertas suelen construir teorías que explican el motivo por el cual, en esa guerra comercial entre los dos productos, que en la mayoría de los casos han iniciado su recorrido en igualdad de condiciones, uno de ellos acaba imponiéndose al otro, o teniendo una ventaja considerable. Desde una reflexión a posteriori se recurren a argumentos de mejor adaptación al medio, mejor calidad, mejores estrategias de venta y marketing, mejor diseño, etcétera … explicaciones racionales y muy acertadas todas ellas, pero que no tienen en cuenta que el azar puede tener una intervención mayor de lo que pensamos.

La urna de Polya

Para intentar comprender un poco mejor las situaciones como las comentadas más arriba, la competición entre dos (aunque podrían ser más) productos, bajo una serie de condiciones, vamos a explicar un modelo matemático, conocido con el nombre de la urna de Polya. Este modelo también se puede aplicar al estudio de otros temas, como la propagación de enfermedades o los comportamientos sociales.

El nombre de este modelo matemático se debe al matemático húngaro, que se nacionalizaría primero suizo y después estadounidense, George Polya (1887-1985), quien investigó en diferentes ramas de las matemáticas, como combinatoria, teoría de números, análisis numérico y probabilidad, aunque también es muy conocido por sus contribuciones sobre heurística y educación matemática, entre otros libros escribió How to prove it / Cómo plantear y resolver problemas (1945), y era miembro del conocido grupo de científicos (mayoritariamente matemáticos y físicos) húngaros que emigraron a Estados Unidos en la primera mitad del siglo xx, como los matemáticos Paul Erdös, Paul Halmos, Peter Lax, John von Neumann o el físico y matemático Eugene Wigner, entre muchos otros, conocido como el grupo de “Los Marcianos” o “Los Marcianos de Budapest”.

Pero describamos el modelo matemático de la urna de Polya.

A. Situación inicial. Se parte de una urna con una cierta cantidad de bolas de dos o más colores.

En esta entrada del Cuaderno de Cultura Científica vamos a considerar el caso más sencillo, bolas de dos colores (por ejemplo, azules y rojas) y que inicialmente haya en la urna una bola de cada color, una roja y una azul.

Además, se debe de tener aparte una bolsa con bolas rojas y azules que sirva de suministro de las bolas que se necesiten para la realización del experimento, que se podría decir que sean infinitas para transmitir que tiene que haber tantas como sean necesarias para la cantidad de acciones que se van a realizar.

B. Extracción y “efecto contagio”. De la urna, que contiene inicialmente una bola roja y una bola azul (en el caso simple que estamos planteando), se extrae una bola al azar. Entonces se mira el color de la bola extraída y se devuelve la bola a la urna, introduciendo en la misma, además, otra bola del mismo color.

Una alternativa, que se comentará más adelante, es que se introduzca una bola del color contrario al de la bola que ha sido extraída. Más aún, se puede considerar el caso más general, de introducir una cierta cantidad de bolas de cada uno de los colores, en función de lo que se quiera modelizar.

C. Situación final. El proceso repite una cantidad considerable de veces, para observar cómo evoluciona la proporción de bolas rojas (respectivamente, de bolas azules) sobre el total de bolas.

Experimentando con la urna de Polya

Una vez que tenemos claro en qué consiste el modelo matemático, podemos realizar un experimento del mismo para ver cómo funciona. Por ejemplo, preparo mi urna con una bola roja y una bola azul, meto mi mano en la urna (sin mirar claro, para que sea una extracción al azar) y saco una bola … que resulta que ha salido roja, entonces la vuelvo a introducir en la urna, junto con otra bola del mismo color, roja, lo que provoca que ahora haya dos bolas rojas y una azul en la urna, esto es, la proporción de bolas rojas es de 2/3 (0,667 sobre 1).

Mientras que en la primera extracción la probabilidad de sacar una bola roja o una bola azul era la misma, de 0,5 sobre 1 (o una probabilidad del 50%), ya que hemos planteado una situación inicial de equilibrio, en la segunda extracción de nuestro experimento la probabilidad de sacar una bola roja es del 66,67% (0,6667 sobre 1), frente a un 33,33% (0,3333 sobre 1) de sacar una bola azul. Meto de nuevo la mano en la urna (de nuevo, sin mirar) y resulta que vuelve a salir una bola roja (lo cual era lo más probable), que devuelvo a la urna junto a otra bola roja. Por lo tanto, la urna tiene ahora tres bolas rojas y una azul. En consecuencia, en la siguiente extracción, la tercera, la probabilidad de sacar una bola roja es mayor aún.

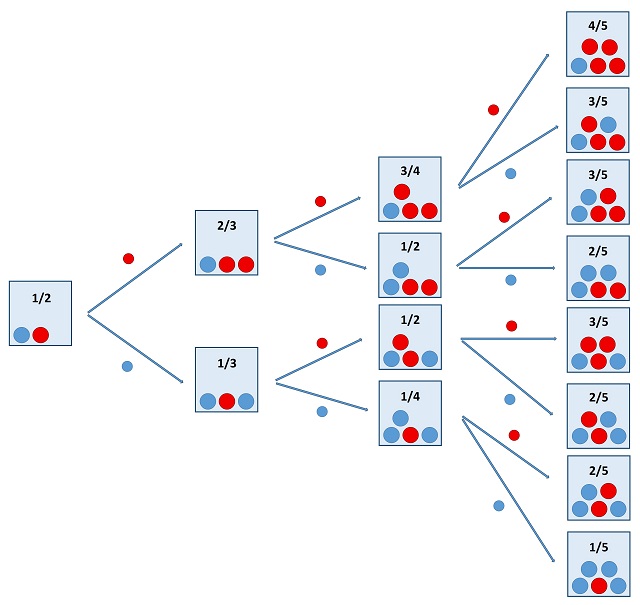
La cuestión ahora es qué pasará si continúo el experimento con muchas más extracciones, cómo evolucionará con el tiempo, es decir, después de una cantidad alta de extracciones qué pasará, habrá más bolas rojas, más bolas azules o tenderemos a un equilibrio entre los dos colores.

El efecto contagio

Expliquemos brevemente lo que hemos denotado como “efecto contagio” en el modelo de la urna de Polya. El nombre de efecto contagio viene del hecho de que, al sacar una bola de un cierto color, la siguiente que introducimos es del mismo color que el de la bola que ha salido, es decir, se contagia el color de la bola extraída a la nueva bola que se va a introducir.

Pensemos en nuestro ejemplo de la propagación de los sistemas de video VHS y Beta. Imaginemos que inicialmente había tan solo dos propietarios de vídeos, uno con el sistema Beta y otro con el sistema VHS. Una tercera persona quiere comprar un reproductor de vídeo y se está cuestionando cuál comprar. Entonces, se encuentra con uno de los propietarios de reproductor de video y éste le cuenta maravillas del sistema de su aparato. Así que, si la persona con la que se ha topado tiene el sistema VHS, la persona interesada adquirirá también un VHS, mientras que, si su sistema es Beta, se comprará un Beta. Supongamos que se ha producido el primer caso, entonces ahora hay dos reproductores VHS y uno Beta. Una cuarta persona entra en juego y de nuevo se pregunta cuál adquirir. Tengamos en cuenta que ahora es algo más probable encontrar a dueños de vídeos VHS, dos frente a uno. Si este nuevo cliente encuentra a una persona con VHS, se unirá al grupo de los usuarios de VHS, y si encuentra a una con Beta, al de los usuarios de Beta. Y así, sucesivamente.

En el modelo que estamos explicando de la urna de Polya, cuando se introduce en la urna una nueva bola del mismo color que la que ha salido, la urna modeliza una situación en la que se favorece “al que más tiene”, a la opción más abundante (en la urna). Esto es así porque el color predominante en la urna es más fácil que salga, es más probable que una bola de ese color sea extraída de la urna, por lo tanto, es más probable que ese predominio aumente al incorporarse una bola del mismo color que la extraída.

Mientras que, en el segundo caso, cuando se introduce en la urna otra bola del color contrario al que ha salido, la urna modeliza una situación en la que se favorece “al que menos tiene”, a la opción menos abundante. Esto es así porque, como decíamos, el color predominante en la urna es más fácil que salga, es más probable que una bola de ese color sea extraída de la urna, por lo tanto, al introducir una bola del color contrario a la sacada, se equilibra un poco la proporción de bolas de cada color.

Realizando muchos experimentos

En el experimento de la urna de Polya que hemos iniciado más arriba, podríamos haber seguido hasta llegar a un número elevado de extracciones, quizás 500 o 1.000 extracciones, ver qué ha pasado e intentar imaginar qué es lo que pasa en general. Pero en ese caso solamente habríamos realizado un experimento. Para poder sacar una información un poco más fiable habría que realizar el mismo experimento muchas veces y observar los resultados. Pero eso nos llevaría a estar varios días o incluso semanas sacando y metiendo bolas en nuestra urna.

¿Qué podemos hacer? Por suerte tenemos nuestros ordenadores que nos permiten hacer simulaciones del experimento de la urna de Polya (por ejemplo, con 500 o 1.000 extracciones cada uno) y además nos permite hacer muchas simulaciones, todo ello en un breve espacio de tiempo, a partir de las cuales intentar sacar conclusiones.

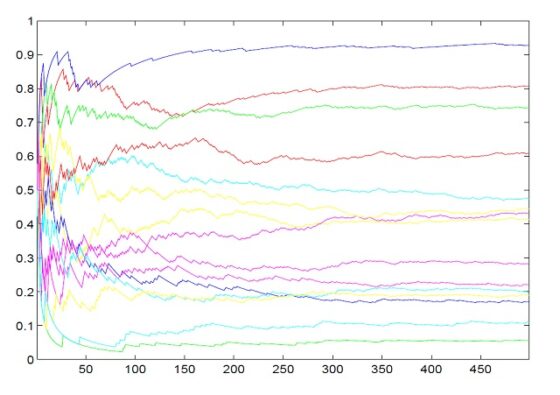
A continuación, vamos a mostrar el resultado de realizar con el ordenador quince simulaciones, con un total de 500 extracciones cada una, del experimento de la urna de Polya, en el caso en el que se favorable “al que más tiene”, a través de un gráfico en el que se representa la evolución en cada simulación de la relación entre bolas rojas y azules. En el gráfico, una relación de 0,5 significa que hay la misma cantidad de bolas rojas que de azules, si la relación es mayor que 0,5 entonces hay más bolas de un cierto color, por ejemplo, rojas, y si es menor que 0,5, habrá más azules.

¿Qué creéis que va a ocurrir? Si sois de la opinión de que, con el paso del tiempo (al aumentar la cantidad de extracciones), se llegará a un equilibrio entre ambos colores, entonces nuestros gráficos tenderán hacia el valor 0,5. Pero si pensamos que habrá más bolas rojas, los gráficos tenderán a algún número entre 0,5 y 1. Si fuese 1 significaría que a la larga desaparecen las bolas azules. Lo mismo, pero al revés para las bolas azules. Si hay más bolas azules, los gráficos tenderán a algún valor entre 0 y 0,5; mientras que 0 significaría que a la larga desaparecen las bolas rojas.

Algunas conclusiones

Comentemos brevemente los resultados del gráfico anterior.

A. Lo primero que podemos observar en el gráfico es que hay experimentos en los que la relación entre bolas azules y rojas está cercana a 0,5, se equilibra. Pero también hay experimentos en los que la relación está por encima de 0,5, incluso cerca de 1, (es decir, predominarán las bolas rojas sobre las azules) y también experimentos por debajo de 0,5, incluso cerca de 0 (i.e. predominan las azules sobre las rojas). En conclusión, este gráfico nos da a entender que puede pasar cualquier cosa. De hecho, eso es lo que dice el resultado matemático teórico (de teoría de la probabilidad), nos dice que para cualquier valor entre 0 y 1 puede darse un experimento que tenga ese valor como relación final entre bolas rojas y azules.

B.También observamos que es en las primeras extracciones donde se produce más variación en la relación entre bolas rojas y azules, pero que luego esa relación se va estabilizando y prácticamente no fluctúa. En conclusión, las primeras extracciones del experimento son las que de alguna forma determinan hacia qué relación final va a dirigirse el experimento, lo cual se produce porque nuestro sistema favorece al que más tiene.

Por lo tanto, de este experimento podemos extraer la conclusión de que en temas de confrontación entre dos productos rivales (como los casos comentados, los sistemas de vídeos VHS y Beta, los sistemas de teclados Qwerty o DSK, las bebidas Coca Cola y Pepsi, las consolas SEGA y Nintendo, entre otros) la relación final de fuerzas o quien dominará el mercado no siempre se justifica únicamente en motivos de calidad, diseño, marketing, etcétera, sino que en ocasiones el azar también juega un papel importante.

Aunque también nos dice el experimento que el inicio determina en gran medida la relación final, motivo por el cual una publicidad agresiva inicial o cualquier otro tipo de ventaja inicial puede determinar quién dominará en el futuro, o si se produce un cierto equilibrio de fuerzas.

Realiza tus propias simulaciones

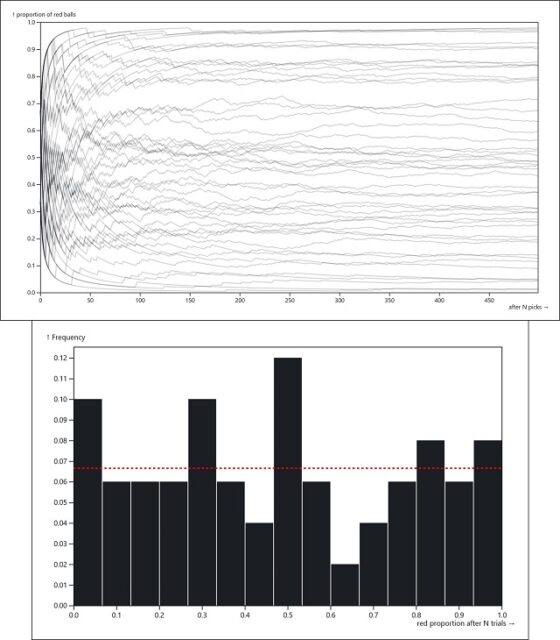
Si estáis interesados en realizar vuestras propias simulaciones del modelo de la urna de Polya y no queréis programarlo vosotros mismos, tenéis algunas opciones. Por ejemplo, en la siguiente página de Charlie Moog sobre la urna de Polya (pincha aquí), podéis plantear la realización de entre 1 y 100 simulaciones distintas, con cantidad de extracciones entre 1 y 1.000, y se generará la representación gráfica instantánea de todas ellas. Además, le acompaña un gráfico de barras para conocer cuántas de esas simulaciones han tenido proporciones de bolas de un cierto color (p.e. rojas) entre 0 y 0,1; entre 0,1 y 0,2; entre 0,2 y 0,3; así hasta entre 0,9 y 1, para entender mejor que todas las opciones entre 0 y 1 son posibles, e igualmente probables.

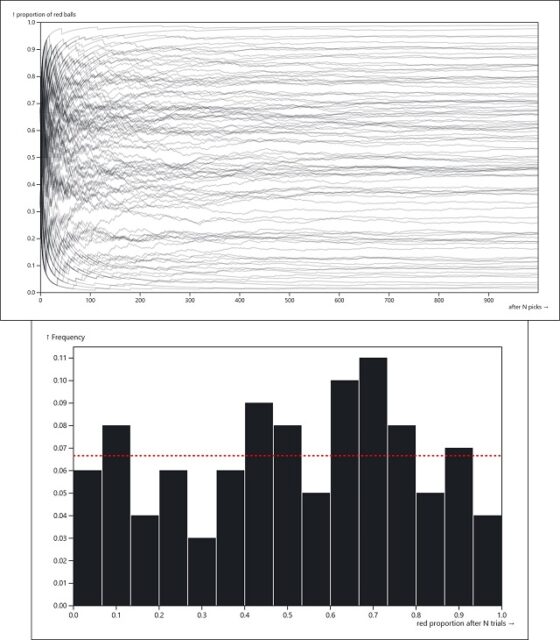
A continuación, mostramos dos imágenes de dos experimentos con la herramienta de la página de Moog, el primero con 50 simulaciones de 500 extracciones cada una de ellas y el segundo con 100 simulaciones de 1.000 extracciones.

Favorecer al que menos tiene

Hemos analizado el caso en el que el modelo de la urna de Polya favorece al que más tiene, esto es, se añade una bola del mismo color que el de la bola extraída, pero podemos plantearnos qué ocurre si el modelo favorece al que menos tiene, es decir, si tras cada extracción se introduce en la urna, además de la bola extraída, una nueva bola del color contrario al de la bola que hemos sacado. ¿Cuál será en este caso la evolución de la relación entre la cantidad de bolas rojas y azules?

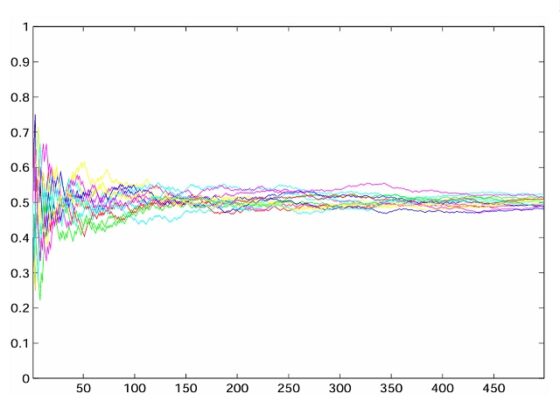
La anterior imagen nos muestra un gráfico en el que se representa la evolución en cada simulación de la proporción de bolas rojas respecto del total de bolas, rojas y azules, al realizar quince simulaciones, con un total de 500 extracciones cada una, del experimento de la urna de Polya, en el caso en el que se favorable “al que menos tiene”.

Aunque parezca mentira, con el paso del tiempo la relación entre la cantidad de bolas rojas y azules tiende a igualarse. La proporción de bolas rojas sobre el total de bolas (rojas y azules) se aproxima a 0,5, es decir, se produce una situación de equilibrio entre los dos colores.

El anterior resultado nos puede llevar a una interesante reflexión sociológica, que nos muestra que favoreciendo al que menos tiene es como llegamos a situaciones de equilibrio.

Un comentario final

En el modelo de la urna de Polya que hemos descrito se consideran únicamente dos colores y en la urna inicial hay una bola de cada color, sin embargo, se puede considerar el modelo más general, con un número cualquiera de colores y una situación inicial diferente, no solo una bola de cada color, sino tantas bolas como creamos conveniente.

Por otra parte, en nuestra descripción del modelo, se han considerado solo dos opciones de contagio, que se favorezca al que más tiene, es decir, se añade a la urna una bola extra del mismo color que el de la que ha salido en la extracción al azar de una bola de la urna, o que se favorezca al que menos tiene, esto es, se añade una bola extra del color contrario al que ha salido. Sin embargo, se pueden considerar situaciones diferentes, que se añadan una cierta cantidad de bolas de cada color, en función de las situaciones que se quieran modelar.

Es interesante realizar simulaciones de todas esas opciones para observar qué ocurre en cada una de ellas. Para lo cual, podéis escribir un pequeño programa que realice las simulaciones, por ejemplo, en Python, si conocéis este o algún otro lenguaje de programación, aunque si no es el caso, siempre os puede ayudar alguna IA a programarlo.

Bibliografía:

1.- M. A. Cusumano, Y. Mylonadis, R. S. Rosenbloom, Strategic maneuvering and mass-market dynamics: The triumph of VHS over Beta, Business History Review, 66 (1), pp. 51-94, 1992.

2.- José Luis Fernández Pérez, La vida es una tómbola: gestión del azar y finanzas, conferencia del ciclo Las matemáticas en la vida cotidiana (Biblioteca de Bidebarrieta, Bilbao), 2006.

3.- Pablo Fernández, Modelizando el azar, Estalmat Madrid

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica