El fútbol es un deporte que levanta pasiones. Por este motivo, no es de extrañar que cuando un equipo de fútbol se clasifica para una final, las personas aficionadas de ese equipo muevan cielo y tierra para conseguir una entrada para el partido. Una entrada para la final se convierte en un pequeño tesoro.

La historia que vamos a contar en esta entrada del Cuaderno de Cultura Científica tuvo lugar hace ya unos años, cuando cierto equipo de fútbol se clasificó para una final importante. Como es comprensible, su afición estaba deseosa de asistir a la misma, pero las entradas para el partido escaseaban. El Club, que disponía de una cierta cantidad de entradas para la final, realizó un sorteo de las mismas entre sus socios, en el que me vi implicado sin ser yo una persona muy aficionada al fútbol.
Al día siguiente del sorteo, un periodista que había estado presente en el desarrollo del mismo se puso en contacto conmigo para que analizáramos juntos algunas de sus cifras, ya que no le cuadraban. A pesar de que yo estaba preparándome para asistir esa misma tarde a un espectáculo del Circo del Sol, saqué el tiempo suficiente para que nos reuniéramos y me explicara todo el asunto.

El club sorteaba 14.800 entradas y se inscribieron 33.301 socios a través de 25.746 solicitudes, ya que cada solicitud podía llevar agrupados hasta cuatro socios distintos, con lo cual si salía elegido su número de solicitud les corresponderían tantas entradas como socios agrupados. De esta forma, puesto que se contabilizaron 25.746 solicitudes de 33.301 socios, se sabía de inicio que había 33.301 – 25.746 = 7.555 socios agrupados como segundo, tercero o cuarto socio de alguna de las solicitudes (que podemos denominar “socios agrupados extra”).
Algo andaba mal
La siguiente información que me proporcionó el periodista, fue que el club había informado el segundo día del plazo para la inscripción que ya se habían apuntado 19.654 socios en un total de 13.449 solicitudes, es decir, ya había 6.205 agrupados extra. La primera conclusión que se podía extraer de esta información, puesto que había en total 7.555 socios agrupados extra, fue que entre los números de las solicitudes 13.450 y 25.746 – es decir, después del segundo día- solamente podía haber 7.555 – 6.205 = 1.350 socios agrupados extra. Este dato resultó ser trascendental para descubrir que algo andaba mal.
Además, el sorteo fue un poco enrevesado. En el mismo se sacaban cinco números y se entregaban 2.960 entradas (1/5 de las 14.800 entradas en total a repartir) a partir de cada uno de ellos, teniendo además en cuenta que había solicitudes con socios agrupados y para una misma solicitud podían corresponderle hasta cuatro entradas. Por lo que las cuentas no cuadraban y así lo reflejó el periodista –que realizó un magnífico trabajo de investigación- en el artículo publicado al día siguiente en el periódico para el que trabajaba:
“Las entradas repartidas entre el número 18.428 y el 19.956 (ambos inclusive) son, según las bases del sorteo, 2.960. Como quiera que ahí solo aparecen 1.529 números de agraciados resulta que en teoría hay 1.431 agrupadas en esta horquilla. Aquí aparece el primer problema matemático. Son 81 más de las en teoría 1.350 asignadas para todos los números situados por encima del registro 13.449.
Entre los números 20.299 y el 24.903, ambos inclusive, hay un total de 4.605 solicitudes para 8.880 entradas, dado que al haberse superpuesto tres números agraciados (20.299, 21.549 y 22.496) a este grupo le corresponden el triple. La resta entre el número disponible y la cifra de solicitudes afortunadas revela que aquí se han agrupado 4.275 personas. Si sumamos esta cifra a los agrupados entre el 18.428 y el 19.956 resulta que los socios ‘concentrados’ desde el segundo día son 5.706, cuando según datos oficiales del club en ningún caso podía ser mayor de 1.350.”
Es decir, podíamos deducir por la información suministrada por el club en el sorteo que la cantidad de socios agrupados extra, con números por encima de 13.450, que habían recibido entradas para la final eran 5.706, pero resulta que solo había 1.350 agrupados extra por encima de 13.450. En conclusión, esta cuenta nos decía que, al menos, 5.706 – 1.350 = 4.356 entradas estaban asignadas a socios agrupados extra inexistentes. Se desconocía que había pasado con ellas. Al día siguiente el club dio a conocer que se había producido un error informático en la asignación de entradas.

La ventaja de empezar por 2
Por otra parte, el método de realización del sorteo también tenía su propio interés matemático. El sorteo no era un sorteo de los llamados “justo”, puesto que no todas las solicitudes, todos los números, tenían las mismas probabilidades de salir elegidos.
Como había 25.746 solicitudes, el club decidió poner 5 urnas. La primera (para las decenas de millar) con 3 bolas -0,1,2-, y las demás con 10 bolas –del 0 al 9- (unidades de millar, centenas, decenas y unidades), aunque con correcciones durante el sorteo, ya que si, por ejemplo, la primera bola era un 2, se quitaban las bolas 6, 7, 8 y 9 de la siguiente urna, ya que la segunda bola solo podía tomar valores entre 0 y 5 (puesto que el número más alto posible era el 25.746), y de forma similar para el resto de urnas.
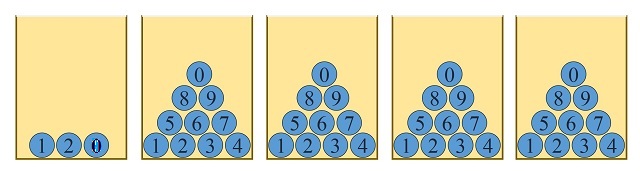
El club no se dio cuenta, a la hora de elegir el método de sorteo, de que con el que se había propuesto, los números que empezaban por 2 tenían más posibilidades de salir que los que empezaban por 0 o 1. Para entenderlo mejor, simplifiquemos un poco y supongamos que tenemos que sacar un número premiado con ese método sobre un total de 20.001 solicitudes. Fijémonos en dos números, A = 13.437 y B = 20.001, ¿tendrán las mismas probabilidades de salir? Para empezar en la primera urna, cada número -0,1,2- tiene las mismas probabilidades de salir (de hecho, 1/3). Si la primera bola es 1, entonces la probabilidad de que salga el número A es de 1 entre 10.000, ya que hay 10.000 números que empiezan por 1 –desde el 10.000 al 19.999-, pero si sale 2 en la primera urna, B tiene una probabilidad del 50% -1 entre 2- de salir, puesto que solamente hay dos números que empiezan por 2 –20.000 y 20.001-.
Efectivamente, el sorteo no era justo, no todos los números tenían la misma probabilidad de salir. De hecho, de los cinco números que se sacaron, tres empezaban por 2.

Bibliografía:
1.- Raúl Ibáñez, Leer el periódico con ojos matemáticos, ConCIENCIAS.digital: revista de divulgación científica de las Facultad de Ciencias de Zaragoza, no. 8, 2011, págs. 48-57.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica