El lenguaje matemático se compone de las letras y los números que forman parte de nuestro lenguaje normal, el que utilizamos para comunicarnos en nuestro día a día, pero también está formado por una cantidad importante de signos matemáticos característicos de esta ciencia. El objetivo de estos signos, que deben ser lo más sencillos posible, es convertir al lenguaje matemático en un lenguaje universal, que no esté sujeto a ningún idioma y que puedan ser entendidos por cualquier persona del planeta, independientemente del idioma que hable o el lugar en el que resida.

Los signos matemáticos, como cualesquiera otros elementos de nuestra cultura, tienen su propia historia, que de hecho es la nuestra, la de la humanidad. En este artículo del Cuaderno de Cultura Científica vamos a centrarnos en el origen de algunos signos matemáticos básicos, que forman parte de nuestro lenguaje normal, los signos para las cuatro operaciones aritméticas elementales, suma, resta, multiplicación y división, y el signo del igual.

Harris tenía una teoría muy curiosa acerca del cuento. Según él, el cuento no vendría a ser más que una simple operación de aritmética. Pero no una operación de cifras, claro, sino hecha a base de sumas y rectas de elementos tales como amor, odio, esperanza, deseo, honor y otros por el estilo. La historia de Abraham e Isaac, por ejemplo, sería una suma de piedad más amor filial. La de Eva, en cambio, sería una resta limpia, amor a Dios menos amor al mundo. Según Harris, además, las sumas suelen dar origen a cuentos con final feliz. Los originados por restas, en cambio, suelen tener finales trágicos. (Obabakoak, Bernardo Atxaga, Ediciones B, 1989)

Los signos + (suma) y – (resta). La primera vez que aparecen los signos + (más) y – (menos) en un libro impreso, que se sepa hoy en día, es en la obra Mercantile Arithmetic, o Behende und hubsche Rechenung au allen Kau manscha, del matemático alemán Johannes Widman (1462 – 1498), publicado en Leipzig en 1489. Sin embargo, Widman no utiliza los signos + y – como símbolos de las operaciones aritméticas suma y resta, sino, dentro de las prácticas comerciales analizadas en el texto, para expresar exceso y defecto de las mercancías, por ejemplo, en el peso de los barriles. En la siguiente imagen vemos “4 + 5” que quiere decir “4 centner + 5 pfund” o “5 – 17” expresando “5 centner – 17 pfund”, donde recordemos que el “centner” y el “pfund” son unidades de peso alemanes, que 1 “centner” son 100 “pfund”, y un “centner” equivale a 50 kilogramos.

Se suele citar el libro de aritmética del matemático holandés Van der Hoeke (siglo XVI) como la primera publicación impresa en la que aparecen los signos + y – como operaciones algebraicas, ya que se suele fechar su publicación en 1514, sin embargo, esta es de 1937 (la fecha de 1514 es un error relacionado con la edición de 1944). Como menciona Florian Cajori, la primera publicación impresa con el significado algebraico de estos signos es el libro de álgebra y aritmética Ayn new Kunstlich Beuch (1518), del matemático alemán Henricus Grammateus (aprox. 1492-1525).

Sin embargo, esta no es la primera aparición de los signos + y –, ya que se pueden encontrar en algunos manuscritos de Alemania, escritos en latín y en alemán, de los últimos veinte años del siglo XV. En la Biblioteca de Dresde existe un volumen de manuscritos (el MS C80) en los que aparecen, quizás por primera vez, los signos + y –. Manuscritos a los que tuvieron acceso tanto Widman, como Grammateus.

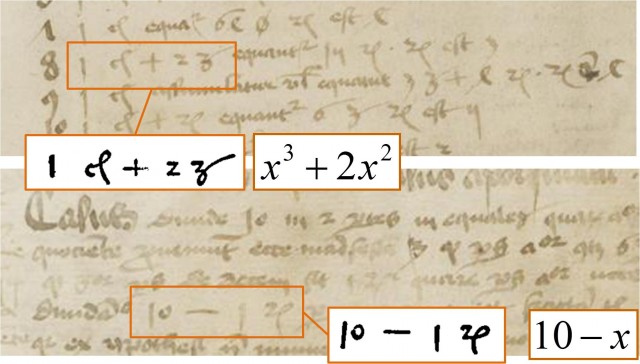
La forma del signo más como una cruz + se debe a que originalmente en los manuscritos latinos se utilizaba la conjunción latina “et”, es decir, la conjunción “y”, para expresar la adición, de la misma forma que nosotros seguimos diciendo hoy en día “2 y 2 son 4”. El signo + es una abreviatura de “et”, de hecho, algunos estudiosos han enumerado más de cien abreviaturas distintas de la palabra “et” en textos latinos, y una de ellas sería la cruz + (pensemos en la escritura de la t). En uno de esos primeros manuscritos, de 1417, aparece una cruz +, pero con el segmento vertical inclinado hacia atrás.

La primera vez que aparece el signo + en un manuscrito podría ser la obra Algorismus proportionum del matemático Nicolás de Oresme (1323-1382), escrito entre los años 1356 y 1361. Sin embargo, es posible también que este signo + haya sido escrito por un copista posterior y no estuviese en la obra original.

El origen del signo – es más incierto, y existen diferentes teorías que tratan de explicarlo. Una de ellas es que podría venir de la utilización de la barra horizontal que los mercaderes utilizaban para indicar la separación de la tara, llamada durante mucho tiempo “minus”, del peso total de una mercancía, es decir, el peso del recipiente del producto. También, podría ser una contracción de la abreviación de la palabra “minus”. Según otra teoría, podría derivar del signo utilizado por el matemático griego Diofanto de Alejandría (siglo III) para el menos, que originalmente era una psi invertida con la parte de arriba recortada, algo así como una cuña como esta , pero con una línea vertical en medio de las dos laterales, que habría derivado a una especie de t mayúscula , que al perder el pie se quedó en el signo –. También podría venir de un símbolo hierático egipcio.

Antes del siglo XV se utilizaron en Italia, como en otros sitios, las palabras más y menos en el idioma de escritura (en latín, “plus” para más y “minus” para menos), de ahí derivaron, por abreviatura las letras “p” y “m” (o estas con una tilde o un segmento encima ) para designar la suma y la resta. Estas abreviaturas, , aparecen por primera vez en la obra “Summa de arithmetica, geometria, proportioni et proportionalita” (1494), del matemático italiano Luca Pacioli (1447-1517), y se siguieron utilizando en los siglo XV y XVI. Los signos alemanes + y – empezaron a utilizarse en Italia ya en el siglo XVII.

El primer uso de los signos + y – en Gran Bretaña fue en 1557 en el libro The Whetstone of Witte, en el que apareció por primera vez el símbolo = para la igualdad. En España y Francia se utilizaban tanto los símbolos alemanes + y –, como los símbolos italianos “p” y “m”.

La cruz + para el símbolo de la suma tuvo también diferentes formas. Por supuesto, la forma principal ha sido la cruz griega, que es la que seguimos utilizando hoy en día. También se utilizó la cruz latina, aunque más frecuentemente utilizada en horizontal (con la parte alargada a la derecha o a la izquierda). Aunque menos, también se utilizaron la cruz que en Escandinavia se llama de San Jorge o la variación de esta que es la cruz de Malta.

A pesar de la sencillez del signo – para la resta, cierto grupo de matemáticos lo sustituyó por el signo más complejo ÷, que fue utilizado durante unos cuatrocientos años, incluso con algunas variaciones, como tener solo el punto de arriba. También se utilizó como signo menos, dos barras seguidas “– –” o tres barras “– – –”.

Por supuesto, antes de estos signos se utilizaron otros para expresar la suma y la resta. Por ejemplo, los babilonios tenían un ideograma en la escritura cuneiforme para la adición (“tab”, que era una cuña-triángulo isósceles- con la punta hacia abajo) y otro para la sustracción (“lal”, una cuña con la punta hacia la derecha). O en el papiro egipcio de Ahmes se utilizan dos piernas caminando hacia delante para el más, y caminando hacia atrás para el menos.

Los signos × y · (multiplicación). Algunos antecedentes de estos símbolos para la multiplicación, como comenta Florian Cajori en su libro, son los siguientes. Los babilonios utilizaban de nuevo un ideograma, llamado “a-du”, para expresar la multiplicación. Diofanto no utilizaba ningún signo. En el Bakhshiili manuscript, el manuscrito más antiguo de las matemáticas de la India, simplemente se pone un factor al lado del otro. El matemático indio Bhaskara Acharia (1114-1185) utilizaba la palabra “bhavita” (o su abreviación “bha”) después de los factores.

Algunos matemáticos, como el matemático alemán Michael Stiefel (1487-1567) en su Deutsche Arithmetica (1545), el matemático flamenco Simon Stevin (1548-1620) o el filósofo y matemático René Descartes (1596-1650) en su Géométrie (1637), utilizan la letra M para la multiplicación y la letra D para la división. Por ejemplo, Stevin o Stiefel escriben la expresión 3①Msec①Mter②, donde sec expresa que es la segunda variable, la incógnita o cantidad desconocida, que aparece y ter la tercera, el círculo con el número expresa la potencia de esa variable, y las letras M y D son la multiplicación y la división, para lo que nosotros denotamos como 3 x y z². O escriben 5②Dsec①Mter② para nuestra 5 x² z² / y.

Por otra parte, el matemático francés Francois Vieta (1540-1603) para expresar el producto de a y b escribía la expresión “a en b”.

La cruz de San Andrés × se utiliza por primera vez como símbolo para la multiplicación en la obra Clavis Mathematicae (1631), del matemático inglés William Oughtred (1574-1660). Aunque se utiliza también en un apéndice anónimo de la traducción de Edward Wright, de 1618, de la obra Descriptio (1614) del matemático escocés John Napier (1550-1617), aunque en este caso en forma de letra x, pero además, este apéndice parece ser que lo escribió el propio Oughtred.

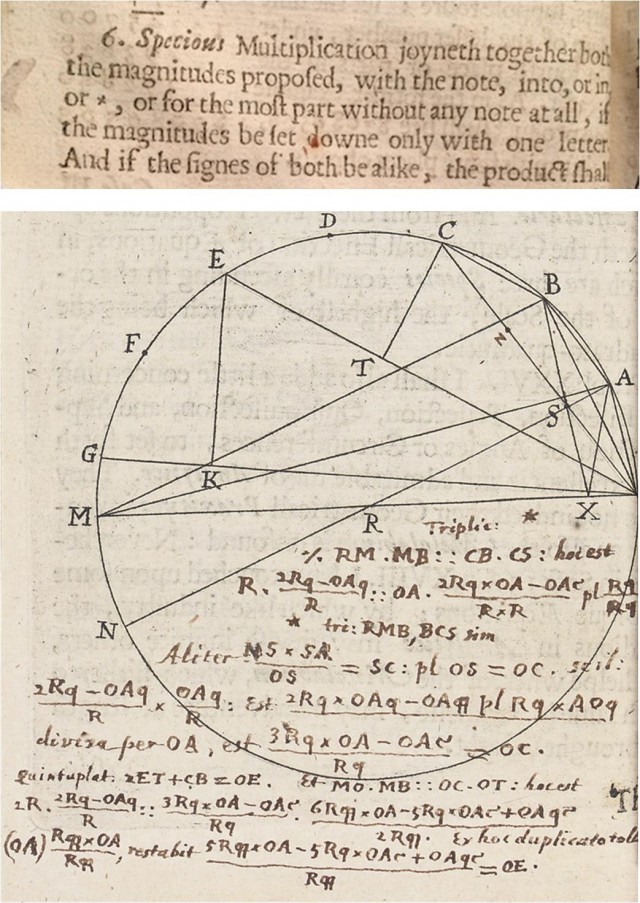
Mientras que Oughtred utilizaba una cruz pequeña, una cruz de San Andrés, el matemático francés Adrien-Marie Legendre (1752-1833), en su Elements de Gèomètrie (1794), utilizaba una cruz grande. El signo ×, para la multiplicación, ha llegado hasta nuestros días, en los que sigue utilizándose, aunque no ha acabado de cuajar del todo, existiendo otro signo que también es utilizado, el punto, fundamentalmente en las matemáticas.

Mientras que en Gran Bretaña tuvo una gran aceptación el signo ×, otros matemáticos, como el matemático alemán Gottfried W. Leibniz (1646-1716), creador junto con el matemático inglés Isaac Newton (1643-1727) del cálculo, no se sentían a gusto con este símbolo. En una de sus cartas al también matemático Johann Bernoulli (1667-1748), de Basilea (Suiza), escribe “No me gusta el símbolo × como un símbolo para la multiplicación, ya que se puede confundir con x;… a menudo yo simplemente relaciono dos cantidades con un punto e indico la multiplicación con RS·PQ”.

Aunque podemos decir que fue Leibniz quien introdujo el punto para la multiplicación, ya había aparecido antes. Por ejemplo, Thomas Harriot en su Artis analyticae praxis (1631) usa el punto en la expresión “aaa – 3 · bba = +2 · ccc”. El punto se adoptaría finalmente como símbolo de la multiplicación en matemáticas a lo largo del siglo XVIII.

Existieron otros símbolos para el producto, así por ejemplo el matemático suizo Johann Rahn (1622-1676) utilizó el asterisco * en su obra Teutsche Algebra (1659) o Leibniz utilizó inicialmente un C tumbada, con la parte abierta hacia abajo, en su Dissertatio de arte combinatoria (1666).

Los signos : y / (división). Al igual que con los anteriores signos, existieron diferentes formas de denotar la división por parte de los babilonios, griegos o los matemáticos de la India, que en muchos casos era la misma que para las fracciones, pero nosotros vamos a centrarnos en los símbolos más modernos que fueron utilizándose para la operación de la división.

Uno de esos signos modernos para la división fue un “signo lunar”, o paréntesis, colocado entre los números. Así, para denotar 24 dividido entre 8 se escribía “8)24”. Este signo lo encontramos en la obra Arithmetica integra (1544) del matemático alemán Michael Stiefel o en el primer diccionario inglés de términos matemáticos del hidrógrafo Joseph Moxon (1627-1691), que escribe “D)A+B–C” para expresar nuestro (A + B – C) : D.

Aunque también se utilizan dos “signos lunares”, o paréntesis, así 24 dividido entre 8 se podía encontrar escrito “8)24(“. Esta notación se siguió utilizando, colocando incluso el resultado de la división a la derecha, al otro lado del paréntesis, así 24 dividido 8 es igual a 3 se expresaba “8)24(3”.

Esta notación para la división se utilizó en los libros de texto de EE.UU. en el siglo XIX.

Como hemos comentado antes, el propio Michael Stiefel empezaría a utilizar las letras mayúsculas M y D para denotar la multiplicación y la división en su obra Deutsche Arithmetica (1545). Otros autores utilizaron también una D, incluso algunos de ellos una D invertida, como el francés J. E. Gallimard (1685-1771), y otros una d tumbada, como el portugués J. A. da Cuhna (1744-1787).

Uno de los signos de la división que ha llegado hasta nuestros días es una barra con un punto arriba y otro abajo ÷. Este símbolo fue introducido por el matemático John Rahn en su obra Teutsche Algebra (1659).

Este símbolo fue muy utilizado en el mundo anglosajón (Gran Bretaña y EEUU), pero no en el continente europeo, y ha acabado cayendo en desuso, aunque sigue siendo conocido. En particular, sigue siendo el símbolo que se utiliza en las calculadoras para la división.

El matemático alemán Gottfried W. Leibniz en su Dissertatio de arte combinatoria (1666) utilizaba una C tumbada, con la parte abierta hacia arriba para denotar la división. Notación que abandonaría para introducir los dos puntos : en su artículo de 1684 en Acta eruditorum, Nova Methodus pro maximis et minimis, itemque tangentibus, et singulare pro illis calculi genus, el primer trabajo en el que se introduce el cálculo infinitesimal. Leibniz explica que para la división va a utilizar la expresión “x : y”, que significa “x dividido por y”, es decir, “”.

Según Leibniz, una de las ventajas del uso de los dos puntos en un texto es que puede mantenerse la división en la misma línea y no hay que introducir espacio extra en la dirección vertical, como ocurre en la notación con la barra horizontal, lo que además hace que se tengan que separar más las líneas.

La anterior cita de la carta de Leibniz a Johann Bernoulli sobre la multiplicación continuaba de esta forma “Para designar la razón no uso un punto sino dos, que también utilizo para la división; así en lugar de tu dy . x :: dt . a escribo dy : x = dt : a, dado que dy es a x como dt es a a es realmente lo mismo que dy dividido por x es igual a dt dividido por a”.

La notación de Leibniz para la multiplicación, el punto ·, y para la división, los dos puntos :, fue rápidamente adoptada en todo el continente europeo.

Pero como vemos Leibniz hace mención, para explicar los dos puntos, a la notación de la división mediante la utilización de la barra horizontal, con dividendo y divisor, arriba y debajo de la barra horizontal. Esta notación que hoy día sigue siendo muy utilizada en el mundo matemático y el no matemático, por su versatilidad para expresar complicadas expresiones, tiene su origen en la antigüedad. Se sabe que la barra horizontal fue introducida por los árabes, aunque se desconoce cómo se introdujo exactamente, o por quién. En Europa fue el matemático Fibonacci, Leonardo de Pisa (1180-1250), quien utilizó por primera vez la barra horizontal (recordemos que fue Fibonacci quien, tras aprenderlos de los árabes, trae a Europa los números indo-arábigos que utilizamos hoy en día).

Por otra parte, la barra diagonal “/”, tan utilizada hoy en día para expresar una división, no fue más que un recurso tipográfico en los libros impresos en el siglo XVIII para expresar la división mediante la barra horizontal.

El signo = (igual). El signo = fue introducido por el matemático Robert Recorde en su libro de álgebra The Whetstone of Witte (1557). Recorde decía que no había dos cosas más iguales que dos líneas paralelas, por ese motivo introdujo el signo = para denotar la igualdad entre dos cosas. Sin embargo, el signo = tardaría bastante tiempo en ser utilizado. No volvió a aparecer en un libro impreso hasta 1618, 61 años después. Y se empezaría a utilizar en Inglaterra a partir del año 1631 en el que se publicaron tres obras muy influyentes que lo contenían, Artis Analyticae Praxis de Thomas Harriot (1560-1621), Clavis Mathematicae de William Oughtred, y Trigonometrie, or the Doctrine of Triangles de Richard Norwood (1590-1675).

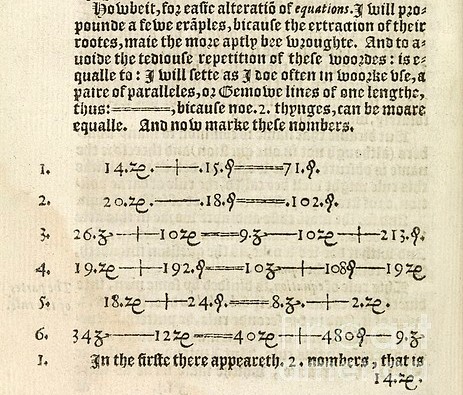
En los libros impresos anteriores a la introducción del símbolo = de Recorde, e incluso más de un siglo después, se utilizaban palabras como “aequales”, “aequantur”, “esgale”, “faciunt”, y otras, para expresar cuando dos cosas eran iguales, incluso la abreviatura “aeq.”. Es decir, algunos autores, como el matemático Vieta escribían “a equale b”, o “a aeq. b”. Y no utilizaban ningún símbolo para la igualdad. Así nos lo encontramos en obras de matemáticos como Kepler, Galileo, Torricelli, Cavalieri, Pascal, Napier, Briggs, Gregory St. Vincent, o Fermat.

El signo introducido por Recorde no solo tardaría en ser asumido por la comunidad científica, en particular la matemática, sino que además se utilizaría el signo “=” con otros significados. Por ejemplo, Vieta lo utilizaría para expresar diferencia, resta de cantidades, así escribiría “9 = 6 aequale 3”. Descartes lo utilizó en 1638 para expresar lo que hoy es el signo ± (es decir, x = ± 1, quiere decir que x es igual a 1 o a -1). E incluso habría otros signos que intentarían introducirse para designar la igualdad de cosas, y no sería hasta el siglo XVIII que el signo de Recorde acabaría imponiéndose en las publicaciones matemáticas, y científicas.

Por otra parte, existían otros signos que competían con las dos líneas horizontales = para expresar la igualdad matemática. Algunos de estos signos fueron el cochete derecho ], dos líneas verticales paralelas ||, una línea vertical |, entre muchos otros.

En la anterior imagen podemos observar dos páginas del libro de Logistica quae & Arithmetica vulgò dicitur in libros quinque digesta … eiusdem ad locum Vitruuij corruptum restitutio, qui est de proportione lapidum mittendorum ad balistae foramen, libro décimo (1559), del matemático francés Joannes Buteo (1492-1572), en la que aparecen por ejemplo las expresiones “1 A,1/3 B,1/3 C[14” y “3 A.3B.15C[120”, que según Florian Cajori en nuestra notación moderna se escribirían como y (y tenemos otras notaciones para la adición, la coma y el punto).

Bibliografía

1.- Alejandro Guijarro, exposición fotográfica Momentum (2010-2013), que puede verse en divulgamat

2.- Florian Cajori, A history of mathematical notations (vol. I, II), Dover, 1993 [originalmente publicado en 1928 por la editorial The Open Court Company, puede encontrarse gratis en la página Internet Archive]

3.- Vicente Meavilla, Eso no estaba en mi libro de Matemáticas, Almuzara, 2012.

4.- Saxon State and University Library Dresden (SLUB)

5.- Jeff Miller, Earliest Uses of Various Mathematical Symbols

6.- Stephen Wolfram, Dropping In on Gottfried Leibniz

7.- Frank J. Swetz, Mathematical Treasure: Leibniz’s Papers on Calculus, Mathematical Association of America

8.- René Descartes, Obras de René Descartes (edición de Charles Adam y Paul Tannery), 1905. Acceso libre en Wikisource

9.- Joannes Buteo, Logistica quae & Arithmetica vulgò dicitur in libros quinque digesta … eiusdem ad locum Vitruuij corruptum restitutio, qui est de proportione lapidum mittendorum ad balistae foramen, libro décimo (1559), Fondo Antiguo de la Universidad de Sevilla

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica