Vivimos en una sociedad digital, en la que los ordenadores, los teléfonos móviles, internet y otros productos tecnológicos digitales inundan nuestra vida, nuestro día a día. En consecuencia, esta revolución tecnológica también se está trasladando a la enseñanza, a las aulas de los centros educativos, aunque algunas personas piensan que este está siendo un proceso más lento de lo que debería ser.

Sin embargo, en mi opinión no debemos desechar las llamadas matemáticas manipulativas, o lo que podíamos llamar “matemáticas para ver y tocar”, puesto que son una herramienta educativa excelente, a todos los niveles de enseñanza, pero principalmente en primaria y secundaria.

Aunque también en la educación universitaria.

La semana pasada estuve leyendo la demostración del siguiente problema, resuelto en 1826 por el matemático suizo Jakob Steiner (1796-1863), ¿Cuál es el máximo número de partes en las que n planos dividen al espacio?, en cuya demostración se hacen uso de las fórmulas de la suma de los primeros números naturales y de la suma de los cuadrados de los primeros números naturales.

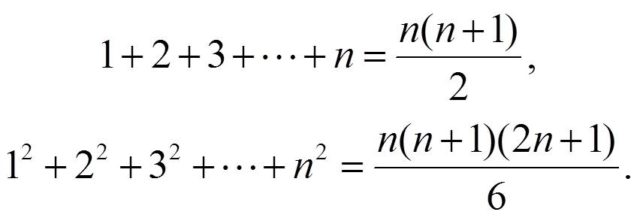
Y me ha parecido interesante traer a la sección Matemoción del Cuaderno de Cultura Científica algunas demostraciones “para ver y tocar” de estas sencillas fórmulas matemáticas. Este tipo de demostraciones se conocen en la literatura matemática como “demostraciones sin palabras”, y ya dedicamos una entrada, Pitágoras sin palabras, a este tipo de pruebas visuales, en concreto, a algunas demostraciones del teorema de Pitágoras.

Comentaba Roger B. Nelsen, autor del libro Demostraciones sin palabras, las demostraciones sin palabras no son realmente demostraciones matemáticas en sí mismas, son más bien diagramas, esquemas o dibujos que nos ayudan a comprender por qué un teorema es cierto o que encierran la idea de la verdadera demostración matemática.

Vayamos con la primera de las fórmulas, la suma de los n primeros números naturales. La primera de las demostraciones visuales se remonta a los griegos, a la época en la que los matemáticos griegos relacionaban los números con los diseños geométricos que se podían realizar con piedras (números triangulares, cuadrados, pentagonales, etc; véase por ejemplo, el artículo La magia de los números (el teorema de Moessner) ). Esta demostración sin palabras la podemos ver en la siguiente imagen, para el caso particular de n = 6.

A mí me gusta trabajar este tipo de demostraciones con pequeños cubos, puesto que así se combina muy bien la prueba visual con el concepto de tocar las matemáticas, en un proceso muy activo de comprensión de la fórmula y su demostración. Una herramienta muy interesante son los cubos del LiveCube, un sistema de cubos para construir puzzles y estructuras geométricas, con los que vamos a trabajar varias de las demostraciones de esta entrada.

La anterior demostración realizada con el LiveCube, para n = 5, sería la siguiente imagen (cada cubo representa una unidad).

Tengamos en cuenta que si trabajamos esta demostración, y otras similares, en un aula de matemáticas o un taller, lo interesante no es solo la imagen final, sino el proceso de construcción de la demostración.

Otra demostración de la fórmula de la suma de los n primeros números naturales se debe al matemático estadounidense Ian Richards, que la publicó en la revista Mathematics Magazine en 1984, y que utiliza cuadrados, algunos de los cuales se cortan por la mitad. Veamos el diagrama para el caso particular n = 7.

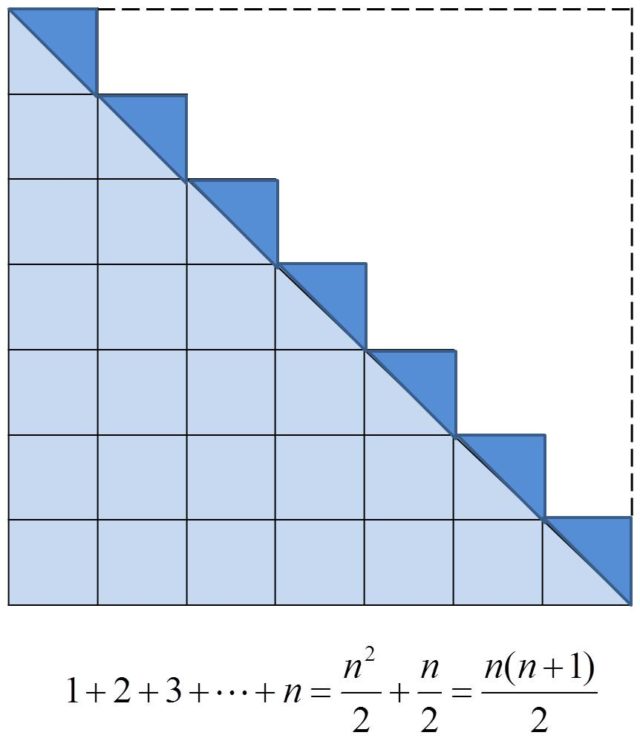
Esto en lo que se refiere a la suma de los n primeros números naturales, aunque podríamos plantear otras sumas similares, como por ejemplo, la suma de los primeros números impares, que resulta ser un número cuadrado. Una sencilla demostración, que en la literatura se atribuye al filósofo y matemático Nicómaco de Gerasa (alrededor del 100 d.c.), es la dada por el siguiente diagrama.

A continuación, vamos a mostrar algunas de las demostraciones visuales que aparecen en la literatura matemática de la fórmula de la suma de los cuadrados de los n primeros números naturales. La primera es una variación de la demostración sin palabras publicada por Man-Keung Siu en Mathematics Magazine en 1984.

Realizamos la prueba para n = 4. Para empezar, consideramos tres copias de una cierta estructura geométrica que refleja la suma de los cuadrados de los 4 primeros números, 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16.

Y después, juntamos las tres estructuras…

… para formar la siguiente estructura compacta, que está formada por un ortoedro (es decir, una caja rectangular) con una base de n = 4 cubos de ancho y n + 1 = 5 cubos de largo, y una altura de n = 4 cubos, es decir, n (n + 1) n = 80 cubos en total, pero además, en la parte de arriba hay 1 + 2 + 3 + 4 cubos más (en general, 1 + 2 + … + n cubos), que aún no habíamos contado.

De donde se deduce la fórmula de la suma de los cuadrados de los n primeros números naturales.

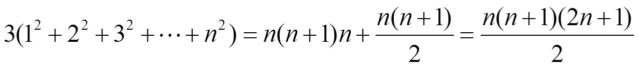
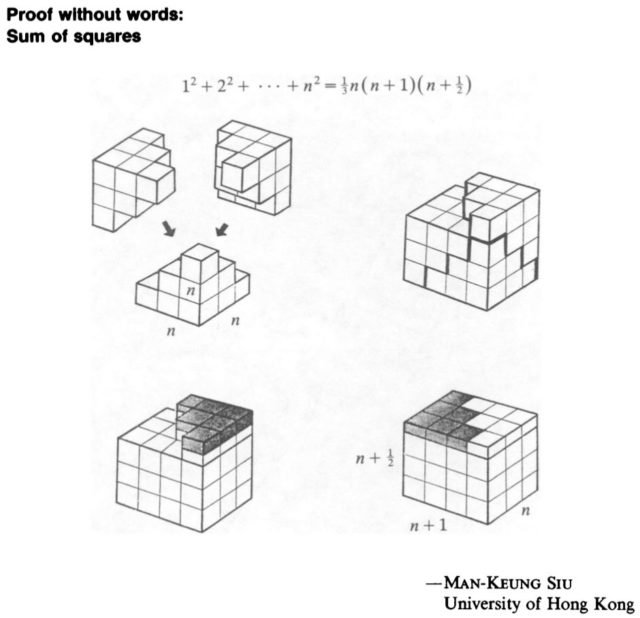
La idea de Man-Keung Siu es la misma, pero en la estructura compacta final anterior, se parten los cubos de la parte superior (que son la mitad de los que cubrirían todo el espacio superior) por la mitad y se rellena la parte que falta de para generar un ortoedro de lados n, n + 1 y n + 1/2, como se muestra en la imagen del artículo original.

Otra demostración sin palabras que podemos ver en el libro de Roger B. Nelsen, demostraciones sin palabras, de la suma de los cuadrados de los n primeros números naturales, obtenida de forma independiente por el gran divulgador de las matemáticas Martin Gardner y el matemático Dan Kalman, es la siguiente, que mostramos para n = 5.

Como se muestra en la imagen, se consideran tres copias de la suma de los cuadrados de los 5 primeros números naturales, 1² + 2² + 3² + 4² + 5², mediante disposiciones geométricas coloreadas de forma diferente para poder seguir el movimiento de los cubos en la siguiente imagen (cada cubo es, de nuevo, una unidad). Observemos que la estructura que está en el medio está coloreada con la idea de que todo número cuadrado n² es la suma de los primeros números impares 1 + 3 + 5 + … + (2n – 1).

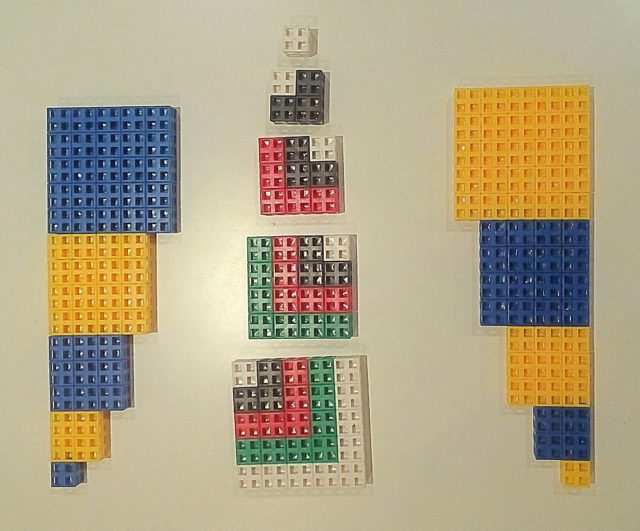
A continuación, se recolocan los cubos de la copia central en función del color, junto con las copias laterales, para obtener un rectángulo, cuya anchura es 11 = 2 n +1 y altura 1 + 2 + 3 + 4 + 5 = 15 = 1 + 2 + 3 + … + n.

Calculando el área del rectángulo, que por una parte es tres veces la suma de los cuadrados de los n primerosnúmeros naturales y por otra el producto de los lados del rectángulo, se obtiene la fórmula deseada.

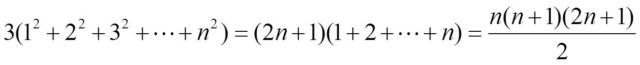
La última demostración sin palabras que voy a mostrar hoy, y que según Roger B. Nelsen, se debe a Nanny Wermuth y Hans-Jürgen Schuch, de la fórmula de la suma de los cuadrados de los primeros números naturales es mi favorita entre las que hemos visto. Es una demostración visual contundente.

Empezamos con tres estructuras geométricas, en cubitos de colores rojo, blanco y verde, que expresan la suma de los cuadrados de los n primeros números naturales, para n = 4. Las dos estructuras de los laterales son bastante evidentes, y la del centro, la blanca, es una estructura que se basa en la idea de que cada número cuadrado se puede expresar como suma de números impares consecutivos, así 1² = 1, 2² = 1 + 3, 3² = 1 + 3 + 5 y 4² = 1 + 3 + 5 + 7.

Juntamos las tres estructuras geométricas. El número de cubos es tres veces la suma de los cuadrados de los n = 4 primeros números naturales.

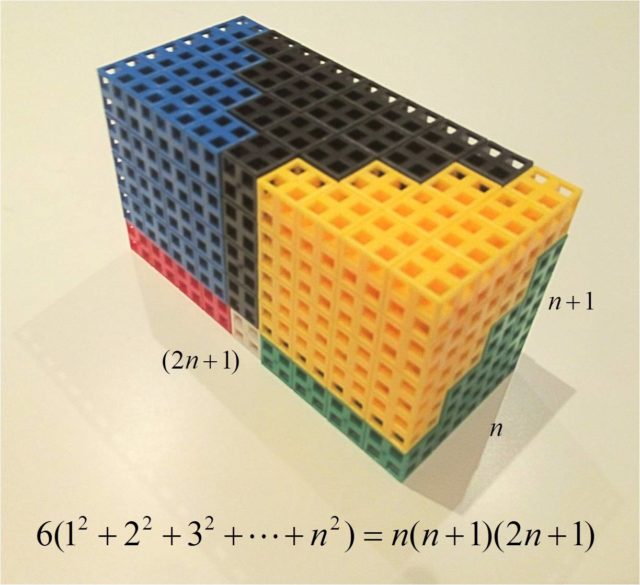
Finalmente, construimos una estructura análoga a esta, pero ahora con otros tres colores diferentes, azul, negro y amarillo, y la colocamos encima de la anterior para formar un ortoedro (caja rectangular) cuyos lados miden (2n + 1), n y (n+1). Por lo tanto, el número de cubos de la estructura final es n (n+1) (2n + 1), y cada una de las seis piezas, que es 1² + 2² + 3² + 4², tendrá la sexta parte.

Para finalizar, os dejo la portada del segundo libro de Roger B. Nelsen sobre demostraciones sin palabras, que incluye la demostración visual de una serie infinita.

Bibliografía

1.- Javier Barrallo, Eiffel Icosa, SIGMA, revista de matemáticas, n. 32, p. 147-158, 2008.

2.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.

3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.

4.- Ian Richards, Proofs without words: Sum of Integers, Mathematics Magazine 57, n.2, p.104, 1984.

5.- Roger B. Nelsen, Proofs without words II, MAA, 2000.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica