El estudio de las ondas y su comportamiento puede que sea más intuitivo si pensamos en grandes modelos mecánicos y en ondas muy simples no periódicas, como los pulsos. Consideremos, por ejemplo, un tren de carga con muchos vagones unidos a una locomotora pero parado. Si la locomotora arranca bruscamente, su tracción sobre el el primer vagón envía una onda de desplazamiento que corre por la línea de vagones.

La perturbación del desplazamiento inicial procede de la locomotora que va haciendo chasquear los acoplamientos uno por uno. En este ejemplo, la locomotora es la fuente de la perturbación, mientras que los vagones de carga y sus acoplamientos son el medio. El «golpe» que viaja a lo largo de la línea de vagones es la onda. La perturbación se desplaza desde un extremo al otro del tren y con ella va la energía del desplazamiento y del movimiento. Sin embargo, ninguna partícula de materia se desplaza con la onda; cada vagón se mueve solo un poco hacia delante.

¿Cuánto tiempo tarda el efecto de la perturbación creada en un punto en llegar a un punto distante? El intervalo de tiempo depende, por supuesto, de la velocidad con la que se propaga la perturbación. Esta velocidad, a su vez, depende del tipo de onda y las características del medio. En cualquier caso, el efecto de una perturbación nunca se transmite instantáneamente. Cada componente del medio tiene inercia y cada parte del medio es compresible. Por lo tanto, se necesita tiempo para transferir energía de una parte a otra. Esto mismo aplica igualmente a las ondas transversales.

La serie de imágenes siguiente representa una onda, un pulso, en una cuerda. Pensemos en cada imagen como un fotograma de una película cinematográfica, y que daca una se ha tomado a intervalos de tiempo iguales. Ya sabemos que el material de la cuerda no viaja junto con la onda. Pero cada parte de la cuerda pasa se mueve hacia arriba y hacia abajo cuando la onda pasa. Cada trozo sufre exactamente el mismo movimiento que el trozo a su izquierda, excepto que lo hace un poco más tarde.

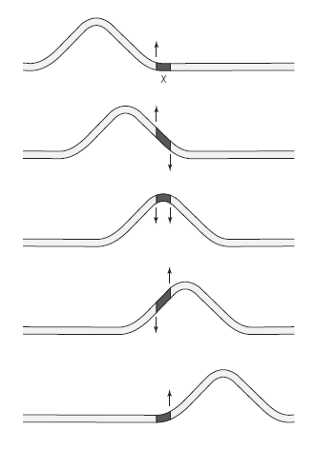
Fijémonos en el pequeño trozo de cuerda señalado con una X en el primer “fotograma”. Cuando el pulso que viaja por la cuerda alcanza X lo que está ocurriendo es que el trozo de cuerda justo a la izquierda de X ejerce una fuerza hacia arriba en X. Cuando X se mueve hacia arriba, el siguiente trozo ejerce una fuerza restauradora (una fuerza hacia abajo). Cuanto más se mueva X hacia arriba, mayores serán las fuerzas restauradoras. Llega un momento en que X deja de moverse hacia arriba y comienza a bajar de nuevo. La sección de la cuerda a la izquierda de X ahora ejerce una fuerza restauradora (hacia abajo), mientras que la sección de la derecha ejerce una fuerza hacia arriba. Por lo tanto, el movimiento hacia abajo es similar, pero opuesto, al movimiento hacia arriba. Finalmente, X regresa a la posición de equilibrio cuando ambas fuerzas han desaparecido.

El tiempo requerido para que X suba y baje, es decir, el tiempo requerido para que el pulso pase por esa parte de la cuerda, depende de dos factores. Estos factores son la magnitud de las fuerzas en X y la masa de X. Dicho de otra manera y en términos más generales: la velocidad con que se propaga una onda depende de la rigidez y de la densidad del medio. Cuanto más rígido sea el medio, mayor será la fuerza que cada sección ejerce sobre las secciones vecinas y, por tanto, mayor será la velocidad de propagación. Por otro lado, cuanto mayor sea la densidad del medio, menos responderá a las fuerzas* y, por tanto, más lenta será la propagación.

De hecho, la velocidad de propagación depende de la relación entre el factor de rigidez y el factor de densidad. El significado exacto “factor de rigidez” y “factor de densidad” es diferente para cada tipo de onda y para diferentes medios. Por ejemplo, para cuerdas tensas el factor de rigidez es la tensión T en la cuerda, y el factor de densidad es la masa por unidad de longitud, m / l, y la velocidad de propagación v viene dada por v = [T / (m / l)]^½

Nota:

*Recordemos que F = m · a, es decir, para una fuerza constante, a mayor masa menor aceleración, que es el efecto que tiene una fuerza que actúa sobre una masa.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance