El problema del puente y la linterna es un rompecabezas de lógica que involucra a cuatro personas, un puente y una linterna.

Pertenece a la familia de los conocidos como puzles de cruce de ríos en los que una serie de objetos deben moverse a través de un río sometidos a determinadas restricciones.

Planteamiento del problema

Cuatro personas —Ángela (A), Boris (B), Carmen (C) y Damián (D)— viajan durante la noche. En cierto momento, deben cruzar un río. El puente que cruza el río es muy estrecho y solo puede sostener a dos personas a la vez. Además, el grupo dispone de una única linterna que necesitan utilizar aquellas personas que van a cruzar el puente.

Las personas A, B, C y D pueden cruzar el puente en 1, 2, 5 y 8 minutos, respectivamente. Todas las parejas de cruzan el puente se desplazan al ritmo de la persona más lenta.

Además, la linterna solo tiene pilas para 15 minutos.

¿Podrán Ángela, Boris, Carmen y Damián cruzar el puente?

Solucionando el problema

Una estrategia que parece lógica es que Ángela, la persona más rápida, acompañe a cada uno de sus compañeros a través del puente. Pero esta táctica requiere demasiado tiempo. En efecto:

1. Al principio A, B, C y D se sitúan en la entrada del puente.
2. A y B cruzan el puente en 2 minutos.
3. A regresa en un minuto al lugar de origen (han transcurrido en total 3 minutos).
4. A y C cruzan en 5 minutos (han transcurrido en total 8 minutos).
5. A regresa en un minuto al lugar de origen (han transcurrido en total 9 minutos).
6. A y D cruzan en 8 minutos (han transcurrido en total 17 minutos).

La linterna se agota antes de conseguir terminar de cruzar el puente. Por lo tanto, esta estrategia no es válida.

Una solución correcta es aquella que minimiza el tiempo de recorrido. Reflexionando brevemente por la estrategia fallida se observa que el problema es que las dos personas más lentas han cruzado el puente en distintos viajes.

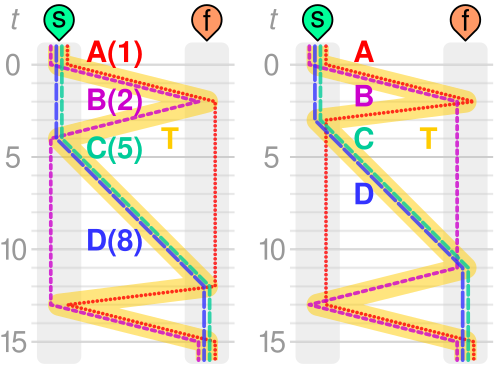
La realidad es que se ahorra tiempo si las dos personas más lentas atraviesan el puente juntas. En efecto, una solución a este problema pasa por usar esta estrategia:

1. Al principio A, B, C y D se sitúan en la entrada del puente.
2. A y B cruzan el puente en 2 minutos.
3. B regresa en 2 minutos al lugar de origen (han transcurrido en total 4 minutos).
4. C y D cruzan en 8 minutos (han transcurrido en total 12 minutos).
5. A regresa en un minuto al lugar de origen (han transcurrido en total 13 minutos).
6. A y B cruzan en 2 minutos (han transcurrido en total 15 minutos).

Una solución alternativa a la anterior es la siguiente:

1. Al principio A, B, C y D se sitúan en la entrada del puente.
2. A y B cruzan el puente en 2 minutos.
3. A regresa en 1 minuto al lugar de origen (han transcurrido en total 3 minutos).
4. C y D cruzan en 8 minutos (han transcurrido en total 11 minutos).
5. B regresa en 2 minutos al lugar de origen (han transcurrido en total 13 minutos).
6. A y B cruzan en 2 minutos (han transcurrido en total 15 minutos).

Nota

Según el matemático Torsten Sillke, el problema del puente y la linterna apareció en 1981, en el libro Super Strategies For Puzzles and Games. En la versión que aparece en esta publicación, las personas que desean cruzar el puente tienen como límite de tiempo 60 minutos, y A, B, C y D tardan en atravesarlo 5, 10, 20 y 25 minutos, respectivamente. La estrategia empleada para encontrar la solución es la misma que en la versión que hemos dado.

Sillke ha investigado la historia de este problema y en su página web ha coleccionado sus hallazgos y referencias sobre el tema hasta 2001. Así, no menciona esta divertida versión de 2022 con unos zombis mutantes que obligan a cuatro personas a cruzar un puente en un tiempo escaso para conseguir escapar…

Existen generalizaciones de este rompecabezas para un número cualquiera de personas con tiempos de cruce arbitrarios. Por ejemplo, en Crossing the Bridge at Night se analiza (suponiendo que la capacidad del puente sigue siendo de dos personas) completamente el problema mediante métodos de teoría de grafos. Como sucede en tantas ocasiones, un sencillo juego de lógica puede dar lugar a interesantes teoremas matemáticos.

Referencias

• Firelight, Futility Closet, 29 octubre 2024
• Bridge and torch problem, Wikipedia
• Saul X. Levmore y Elizabeth Early Cook, Super Strategies For Puzzles and Games, Garden City, N.Y.: Doubleday,1981
• River crossing puzzle, Wikipedia
• Günter Rote, Crossing the Bridge at Night, Bulletin of the European Association for Theoretical Computer Science 78 (2002) 241–246

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y editora de Mujeres con Ciencia