Desde que en el año 2005 los sudokus se convirtieran en uno de los pasatiempos más populares del mundo, se han desarrollado una infinidad de rompecabezas con números, emparentados de alguna forma con el popular sudoku.

En el Cuaderno de Cultura Científica ya hemos hablado en alguna ocasión del sudoku (en la entrada Sudokus, matemáticas y arte contemporáneo), así como de algunos otros rompecabezas con números, algunos de ellos desarrollados después de enorme éxito del sudoku. En la entrada Rompecabezas matemáticos con números hablamos de los rompecabezas sujiko, suko, KenKen, hitori y numberlink, mientras que en la entrada Más rompecabezas matemáticos con números explicamos los rompecabezas inshi no heya (cajas de factorización), hashiwokakero (construye puentes o simplemente puentes), shikaku (divide por cajas), slitherlink (loop / lazo) y akari (light up / iluminar).

En esta entrada, teniendo en cuenta que estamos en verano y es tiempo de relax (cuando tengamos vacaciones, claro), vamos a recuperar el tema de los rompecabezas con números, presentando otros interesantes y entretenidos rompecabezas.

El rompecabezas binario

Aprovechando la tira cómica anterior, vamos a empezar por un rompecabezas de tipo sudoku, pero cuyas entradas son solo ceros (0) y unos (1). Este rompecabezas se conoce con distintos nombres como el rompecabezas binario (puesto que utiliza ceros (0) y unos (1), las cifras básicas del sistema de numeración binario), binairo, binero, sudoku binario, takuzu, Tohu wa-Vohu (expresión hebrea que aparece en la narración sobre la creación en el Libro del Genesis (Torá y Biblia), que podría traducirse como desordenada y vacía, además esta versión suele utilizar los símbolos T y V), Eins und Zwei (que en alemán significa uno y dos, puesto que en esta versión se utilizan estos dos números en lugar de las cifras binarias), tic-tac-logic (inspirándose en el clásico Tic-Tac-Toe, tres en raya, en el que se utilizan los símbolos cruz (X) y círculo (O)), entre otros.

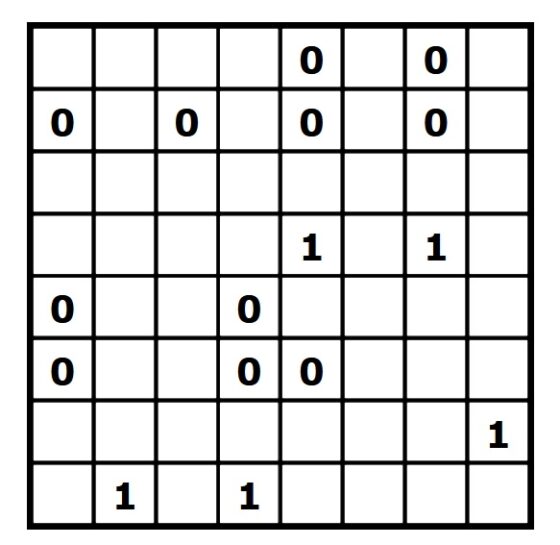
El juego está formado por una retícula, normalmente cuadrada (de tamaño n x n, donde el valor para n suele variar entre 4 y 20, pero puede ser mayor), aunque podría ser rectangular, con unos (1) y ceros (0) en algunas de las casillas de la retícula, que son las pistas iniciales del rompecabezas. Este juego solitario consiste en colocar en cada casilla libre un uno (1) o un cero (0), de manera que se cumplan las siguientes condiciones:

A.- cada fila y cada columna debe de tener el mismo número de unos (1) y ceros (0);

B.- más de dos unos, respectivamente ceros, no pueden ser adyacentes, ni en horizontal, ni en vertical;

C.- cada fila y cada columna son únicas, es decir, no puede haber dos filas iguales, ni dos columnas iguales.

Además, todo rompecabezas binario tiene solución única.

La primera condición nos dice que cada fila y cada columna debe de tener el mismo número de unos (1) y ceros (0), luego hay tantos unos, como ceros, y son la mitad de las casillas de cada fila y cada columna, es decir, la mitad de n. Por lo tanto, n tiene que ser par, como en el ejemplo de la imagen de arriba que es 8 x 8.

Comentemos, con el ejemplo anterior, que es sencillo, cómo se resuelve el binairo. Rápidamente podemos observar que la regla B (no es posible colocar más de dos unos o ceros adyacentes) nos permite deducir algunas de las posiciones. Por ejemplo, en horizontal, en las filas 1 y 2, en los huecos entre dos ceros, hay que poner un 1. La segunda fila se quedaría con cuatro ceros, tres unos y la última casilla vacía, que por la regla A tiene que ser un 1. En las filas 4 y 8, entre los dos unos, tiene que ir un cero, por la regla B. Por la misma regla, en la fila 6, antes y después de los dos ceros consecutivos irán unos. Y lo mismo se hará en vertical, con las columnas.

A partir de ahí tendremos varias casillas ya rellenas que incluso nos permitirán hacer uso de la regla B de nuevo fácilmente. Con un poco de lógica y utilizando las tres reglas se concluye el rompecabezas.

Efectivamente, este rompecabezas es bastante moderno. Los creadores de juegos belgas Peter de Schepper y Frank Coussement registraron el juego “binairo” en la Unión Europea en abril de 2009. Por otra parte, en la página de acertijos y rompecabezas de Angela y Otto Janko, se menciona al inventor de rompecabezas italiano Adolfo Zanellati como el creador del Tohu wa-Vohu, aunque sin citar fecha o fuente de esa creación.

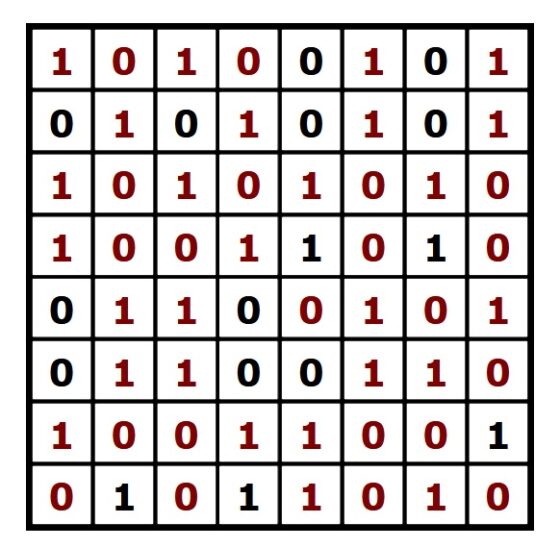
Pero como jugar es lo mejor, os dejo aquí un sudoku binario de tamaño 14 x 14 (clasificado como difícil en la página Binarypuzzle.com de donde lo he sacado), para que paséis un buen rato. Aunque para más binairos no tenéis más que buscar en las muchas páginas donde se publican.

El rompecabezas nurikabe

Cuando resolvemos el sudoku binario lo que nos queda es una retícula binaria, con las casillas con unos (1) y ceros (0), o en otras versiones, con cruces y círculos (tic-tac-logic), o con Ts y Vs (Tohu wa-Vohu), por lo que he pensado en otro juego cuya solución también es binaria en la retícula base, en este caso, casillas negras y casillas blancas. El juego al que me refiero se llama nurikabe.

Por lo que he podido leer, este juego fue inventado por la empresa japonesa Nikoli. Esta editorial tiene una revista de rompecabezas lógicos, que fue publicada por vez primera en agosto de 1980, llamada también Nikoli, aunque su nombre completo es Puzzle Communication Nikoli, que es una revista de pasatiempos muy importante en Japón, pero que adquirió fama mundial por el sudoku. Además, los rompecabezas de la editorial Nikoli son famosos en todo el mundo. El primer nurikabe se publicó en la revista Nikoli en marzo de 1991 (volumen 33).

El nombre de nurikabe deriva del “nurikabe”, que es un espíritu del folclore japonés que, como dice la Wikipedia, “se manifiesta como un muro (invisible) que impide o desvía las rutas de los viajeros durante la noche siendo inútil el intento de rodearlo”.

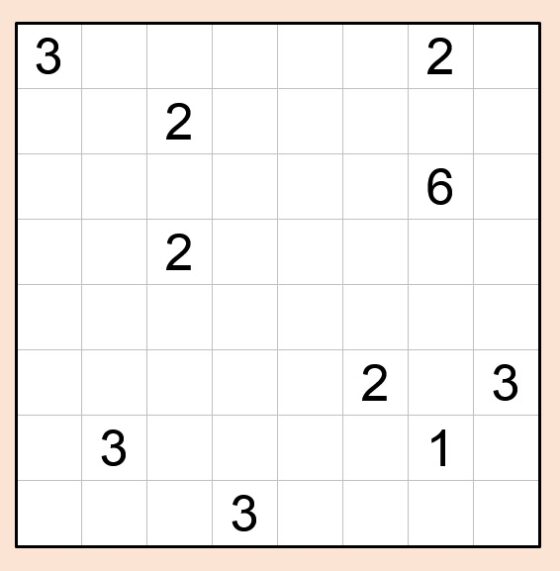
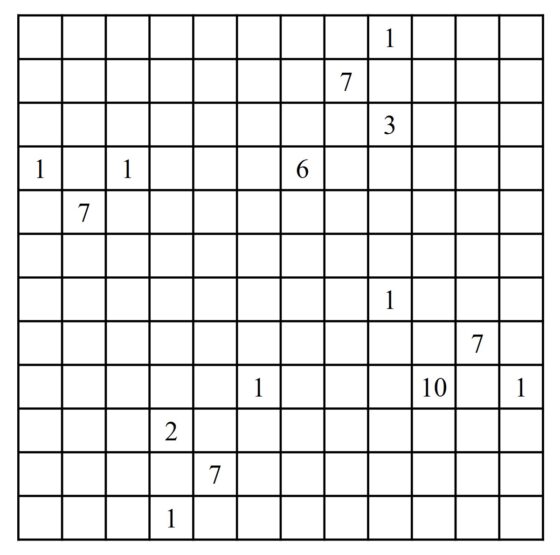
De nuevo, el rompecabezas está formado por una retícula cuadrada (aunque puede ser rectangular) cuyas casillas son todas blancas, aunque en algunas de ellas hay números, como en la imagen anterior.

El jugador deberá pintar algunas de las casillas de la retícula de negro y las restantes quedarán, por tanto, blancas, siguiendo las siguientes reglas:

A.- el objetivo del jugador es crear una serie de “islas” formadas por casillas blancas conectadas (dos casillas están conectadas si comparten un mismo lado, ya sea horizontal o verticalmente);

B.- cada una de las islas debe de tener tantas casillas blancas como el número indicado en una, y solo una, de las casillas de la misma;

C.- no pueden existir zonas de casillas negras conectadas de tamaño 2 x 2, o que incluyan una tal zona;

D.- cuando se finalice el rompecabezas, formando las correspondientes islas (de casillas blancas), las casillas negras estarán conectadas formando un camino continuo.

Si nos fijamos en el nurikabe anterior, la solución constará de una isla de 6 casillas (blancas), cuatro islas de 3 casillas (blancas), otras cuatro con 2 casillas (blancas) y una más, con una única casilla (blanca). Podríamos decir más, puesto en inicialmente hay 64 casillas blancas y las islas ocupan 6 + 16 + 12 + 1 = 35 casillas blancas, deberemos de pintar de negro 64 – 35 = 29 casillas, para resolver el problema.

El punto de partida, como siempre, es ir pintando de negro las casillas que son más evidentes. Por ejemplo, las cuatro casillas adyacentes a una casilla con el número 1, para crear la correspondiente isla, o las casillas adyacentes a dos casillas con números (o incluso casillas como la que está entre el 3 de la esquina y el 2 más próximo), que tiene que ser negra para no unir ambas islas. También irán de negro aquellas casillas que estén muy alejadas de las casillas con números y no puedan formar parte de ninguna isla, como las casillas 4 y 5 de la primera columna.

Y así se va avanzando poco a poco. Por ejemplo, la casilla debajo del seis va a ser adyacente a la isla del 3 de la derecha, puesto que esa isla solo puede subir para arriba, por estar cerca de la del 1, que está rodeado de casillas negras. La casilla que está en la fila 5, columna 5, empezando por arriba a la izquierda, solo puede alcanzarse con la isla del 6, pero en ese caso se uniría a la isla del 2, que no es posible, luego es negra.

Y poco a poco, se va avanzando, teniendo en cuenta que no puede haber cuatro casillas negras formando un cuadrado (2 x 2), por ejemplo, como las casillas 4 y 5 de la primera columna son negras, una de las casillas adyacentes, 4 y 5, de la segunda columna tendrá que ser negra y la otra blanca, pero viendo las dos opciones posibles se llega, rápidamente, a que la casilla debajo del 2 cercano debe ser negra, así como la que está a su derecha.

Y seguiríamos, teniendo en cuenta cada vez más la propiedad C, no puede haber cuatro casillas negras formando un cuadrado, y la propiedad D. Por ejemplo, esta última puede utilizarse para saber que la casilla de la fila de abajo, que está junto a la esquina negra es la única conexión posible con esa esquina y tendrá que ser negra para que la esquina no se quede aislada y se incumpla la propiedad D. De la misma forma, la casilla que está encima del 1 tendrá que conectarse de alguna forma para no quedarse aislada y la única manera es que la que está encima de ella sea negra. Este paso nos abre más opciones. Poco a poco iremos avanzando hasta obtener la solución que se muestra en la siguiente imagen.

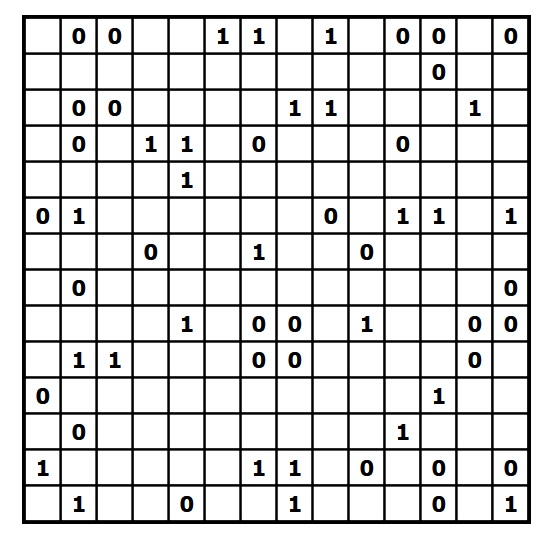
Para terminar este apartado, os dejo un nurikabe de tamaño 12 x 12, clasificado como difícil en la página en la que lo he cogido y en la que podéis encontrar más rompecabezas: nurikabe [https://es.puzzle-nurikabe.com].

El rompecabezas str8ts

Como último juego de esta entrada presentamos otro juego bastante conectado con los sudokus, o quizás más, con los cuadrados latinos (véase la entrada Cuadrados latinos, matemáticas y arte abstracto), el rompecabezas str8ts. Recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n, de tal forma que cada número aparece una vez, y sólo una vez, en cada fila y cada columna. Por lo tanto, las soluciones de los sudokus son cuadrados latinos.

El juego str8ts fue inventado en 2008 por el diseñador de juegos de ingenio canadiense Jeff Widderich.

El juego consiste en una retícula cuadrada 9 x 9 con casillas blancas, algunas de ellas con números entre 1 y 9 (que son las pistas) y algunas casillas negras. En cada casilla blanca debe escribirse un número entre 1 y 9 siguiendo las siguientes reglas:

A.- en cada fila y en cada columna no puede repetirse ningún número;

B.- los números que aparecen en las casillas negras tienen que tenerse en cuenta para la regla A, es decir, no podrá repetirse en la fila y columna en la que está;

C.- cada compartimento, es decir, conjunto de casillas blancas consecutivas de una fila o columna, debe de contener una secuencia de números consecutivos, en cualquier orden (por ejemplo, en la primera fila del str8ts de la anterior imagen hay dos compartimentos, el segundo es 3-2, que ya están colocados como pista, pero en el primero hay un 6 en la casilla central, será una secuencia de tres números que incluya al 6, que no puede incluir al 7 ya que las columnas 3 y 5 ya contienen al 7, luego la secuencia es 4, 5 y 6, pero el orden final va a ser 4-6-5).

Para empezar a resolver este rompecabezas lo mejor es empezar por los compartimentos más pequeños. Por ejemplo, en la última fila hay dos compartimentos de 2 y 3 casillas, con dos pistas, un 5 en una casilla negra (luego ese número no puede utilizarse) y un 7 en la primera casilla del compartimento de tres casillas, en el cual habrá tres números consecutivos del conjunto {6, 7, 8, 9}, pero como en la séptima columna ya están el 8 y 9, tendrán que ser los números 6, 7 y 8, con el orden 7-8-6, ya que el 8 no puede ir, por lo comentado, en la tercera casilla. Respecto al primer compartimento, serán dos números consecutivos del conjunto {1, 2, 3, 4}, pero el 1 no puede ser ya que ya está en las dos columnas de esas posiciones. De hecho, será 3-2, como se ve en la solución que os dejo aquí.

Y para finalizar os dejo uno más difícil para que os divirtáis. En cualquier caso, podéis buscar en internet otros str8ts de diferentes dificultades para jugar y aprender a jugar con la práctica.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica