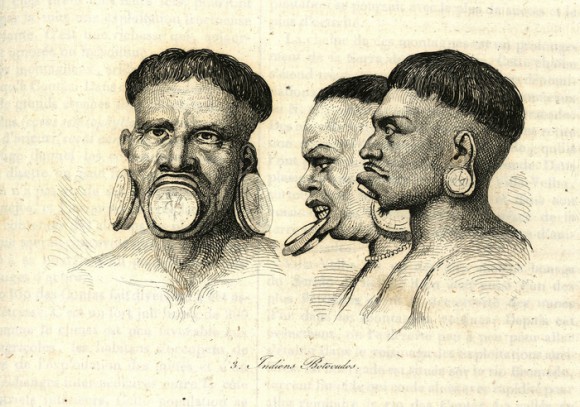
Hace algunos años, leyendo en la biblia de los números, es decir, la Historia universal de las cifras de Georges Ifrah, sobre sistemas de numeración antiguos, descubrí que en el siglo XX aún existían pueblos “primitivos” cuyos sistemas para contar eran muy básicos, ya que prácticamente solo disponían de palabras para el “uno” y el “dos”. Entre ellos se citaba a “los bosquimanos del África austral, los zulúes y los pigmeos del África central, los botocudos del Brasil, los indios de Tierra de Fuego, los kamilarai y los aranda de Australia, los indígenas de las Islas Murray o los vedas de Ceilán”.

Recientemente, hablando de estos temas con una amiga, esta llamó mi atención sobre el hecho de que los bosquimanos eran precisamente el pueblo que aparecía en una conocida película de los años ochenta, “Los dioses deben de estar locos”.

“Los dioses deben de estar locos” fue una comedia de bajo presupuesto, realizada en Botsuana y Sudáfrica, que sorprendentemente cosechó un gran éxito internacional. Una de las tres historias que se entremezclan en la película tiene como protagonista a una aldea de bosquimanos del desierto de Kalahari, un pueblo sencillo que lleva una vida feliz en comunidad, cazando y recolectando lo que los dioses les proporcionan. Sin embargo, un día una avioneta que pasa por encima de la aldea, arroja una botella de coca cola y los bosquimanos interpretan que ese objeto desconocido es un “regalo enviado por los dioses”. Rápidamente, la botella de cristal se convierte en un objeto indispensable para estos indígenas, para tejer cuerdas, curtir la piel de los animales, moler o preparar comida, o como instrumento musical, transformándose a la larga en un objeto de discordia y generador de problemas entre los habitantes de la aldea.

Aquí podéis ver parte de la escena de la botella:

Los bosquimanos, cuyo nombre deriva del afrikáans boschjesman, “hombre del bosque”, y que también reciben otros nombres como san, basarawa o !kung, son, al parecer, el pueblo vivo más antiguo de la Tierra (según recientes estudios se separaron de otros pueblos africanos hace más de 100.000 años). En la actualidad hay, según la wikipedia, unos 90.000 bosquimanos en toda África: 55.000 en Botsuana, 27.000 en Namibia, 10.000 en la República Sudafricana, menos de 5.000 en Angol, y unos pocos en Zambia y Zimbabue. Recientemente han estado en los medios de comunicación debido a que el gobierno de Botsuana los expulsó a los 1.500 sans de la Reserva de Caza de Kalahari Central, como podéis leer en la página web Survival.

Pero volvamos a las matemáticas, y al sistema de numeración de los mencionados bosquimanos de Kalahari. Estos, como muchos otros pueblos “primitivos” de los que vamos a hablar en esta entrada del Cuaderno de Cultura Científica, tenían un sencillo método para contar por pares. Este consistía en disponer de un nombre para los números “uno” (1) y “dos” (2), y a partir de ellos dar nombre a los demás números como composición aditiva de estos, es decir, el número 3 recibía el nombre 2 + 1, el número 4 se nombraría 2 + 2, para el 5 se utilizaría la expresión 2 + 2 + 1, y así hasta el número más alto que utilizaran.

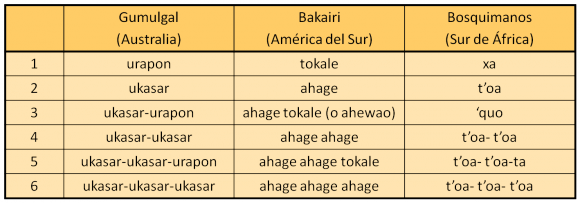
Según he leído en el texto “Numbers through the ages” de Graham Flegg, las palabras de la lengua de los bosquimanos para los números “uno” y “dos” eran [xa] y [t’oa]. Incluso tenían una palabra específica para el número “tres”, [‘quo], pero a partir de ahí utilizaban el sistema de contar por pares, 4 era [t’oa – t’oa] (4 = 2 + 2), 5 [t’oa –t’oa– ta] (5 = 2 + 2 + 1) o 6 [t’oa – t’oa – t’oa] (6 = 2 + 2 + 2). Este método les permitía contar hasta el número 10 = 2 + 2 + 2 + 2 + 2, pero no podía ser utilizado para números más grandes por la complejidad de saber cuántos doses aparecen en la pronunciación del número (y aún así el 10 ya es bastante complicado).

Pero había sistemas aún más sencillos entre esos pueblos “primitivos” del siglo XX que mencionaba Ifrah en su libro, para los cuales cualquier cantidad mayor que 4 era considerada “muchos”. Así, la lengua de los botocudos de Brasil solamente contenía dos vocablos de números, uno para la unidad (1) y otro para el par (2), con ellos podían generar los nombres de los números 3, como “dos y uno”, y 4, como “dos y dos”. Cualquier cantidad mayor que 4 les parecía un número enorme. Para que nos hagamos una idea, Ifrah sugiere que es como si a nosotros nos hablasen de un “trillón de billones”. De hecho, para cantidades mayores que 4 los botocudos se señalaban la cabellera como dando a entender “es una cantidad tan grande como el número de pelos de la cabeza”.

Los arana de Australia tenían un sistema tan simple como el de los botocudos. Ninta era la palabra que utilizada como nombre para el “uno” y tara el nombre para el “dos”. Los números 3 y 4 se decían “tara-mi-ninta” (dos y uno) y “tara-ma-tara” (dos y dos). De nuevo, más allá del número cuatro se utilizaban expresiones que podríamos traducir como “muchos”. Los indígenas de las islas Murray utilizaban las palabras netat y neis para “uno” y “dos”, por lo que “neis-netat” era la palabra para expresar el 3 y “neis-neis” para el 4, y para cantidades mayores una expresión que quería decir algo así como “un montón”. Y para ciertas tribus del estrecho de Torres las palabras básicas eran urapun (uno) y okosa (dos).

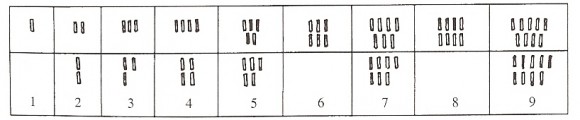
Todo sistema de numeración, por muy básico que sea, cuenta con el número “uno”, puesto que el 1 es el generador básico de todos los demás números, mediante la simple operación aditiva (4 = 1 + 1 + 1 + 1, 7 = 1 + 1 + 1 + 1 + 1 + 1 + 1). Como ya mencionamos en la entrada anterior “Teorías fantásticas sobre el origen de la grafía de los números”, los sistemas de numeración más antiguos representaban los números como una acumulación de rayas, es decir, de suma de “unos”.

Pero como acabamos de ver en los ejemplos anteriores, existieron, y existen, pueblos “primitivos” cuya lengua, además del omnipresente vocablo para la unidad (1), contiene solo un vocablo numérico más para la paridad (2). Y es mediante la composición de estos que se pueden generar los nombres de algunos otros números (2 + 1, 2 + 2, 2 + 2 + 1, etc). Además, cada una de estas lenguas suele contener un vocablo que significa “muchos”, utilizado para referirse a cantidades mayores que el número concreto más alto que es comprendido por ese pueblo.

La importancia del concepto de paridad en muchos de estos pueblos “primitivos” puede ser consecuencia de que el ser humano se miró a sí mismo para descubrir que llevaba consigo el concepto de paridad. Tenemos dos manos, dos brazos, dos pies, dos piernas, dos ojos, dos orejas, dos cavidades nasales, dos mamas, etc. El cuerpo humano está formado por dos partes, la derecha y la izquierda, fruto de nuestra simetría “bilateral”.

Cuando observamos el sistema de contar por pares (también llamado el principio de base dos) que tienen muchos pueblos “primitivos”, este nos recuerda al sistema binario, pero como si fuese una versión primigenia y limitada.

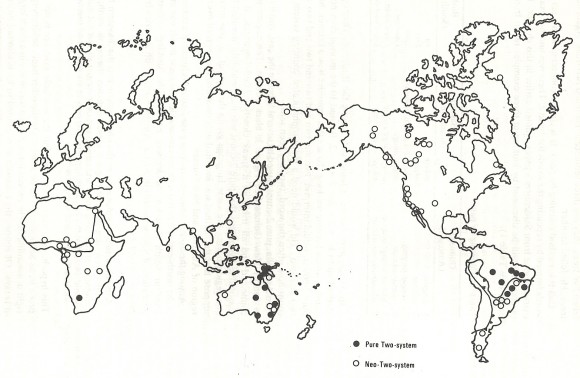
Como puede observarse en el siguiente mapa, del libro de Graham Flegg, el sistema de contar por pares se ha encontrado en pueblos de tres grandes zonas del mundo: Australia (los pueblos narrinyeri del sur, kuri del norte, minyung, kana, kohoyimidir, kauralgal, gumulgal e indígenas del estrecho de Torres) y Nueva Guinea (parb, sisiami y arop), America del Sur (zamuco, arara, bakairi, cayapocrengez, apinage, krao, canella y cotoxo) y en el sur de África (bosquimanos).

Veamos un ejemplo de cada una de las zonas del mundo donde hay pueblos que utilizan el sistema de contar por pares, y de las palabras que utilizan en sus lenguas.

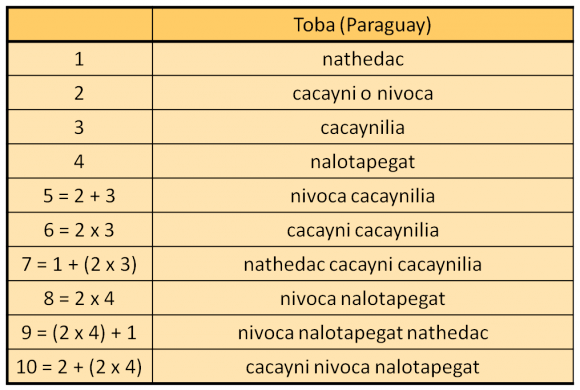
Pero si pensamos que estamos hablando de pueblos con sistemas de numeración muy simples nos daremos cuenta de que en los sistemas puros de contar por pares les sería difícil diferenciar entre la pronunciación de 2 + 2 + 2, que da nombre al 6, y de 2 + 2 + 2 + 2, que da nombre al 8, y más aún diferenciar a estos de la pronunciación para el número 10, es decir, 2 + 2 + 2 + 2 + 2. Por este motivo, muchos otros pueblos (véanse en el mapa anterior los puntos blancos) desarrollaron sistemas de contar por pares modificados, en los cuales el número 6 sería “dos veces tres” -o “tres veces dos”- (2 x 3) y el 8 “dos veces cuatro” -o “cuatro veces dos”- (2 x 4), o cuando llegaban hasta 10 este era 2 x 5. Mientras que para los números impares se podía seguir la regla de añadir 1 al número par anterior, como en el sistema puro, así 7 sería 6 + 1 = 2 x 3 + 1 (dos veces tres más uno) y 9 = 8 + 1 = 2 x 4 + 1 (dos veces cuatro más uno). Este es el caso de pueblos como los payagua o los toba de América del Sur, los wintun de América del Norte o los indígenas del grupo de islas Radak de las Islas Marshall.

Pero mencionemos un ejemplo concreto de los nombres que utilizaban uno de estos pueblos, los toba de Paraguay, para designar los números del 1 al 10.

Aunque también han existido otras formas de generar el nombre con el que referirse a cada uno de los números impares, por ejemplo restando una unidad al número par siguiente, así 7 = 8 – 1 y 9 = 10 – 1, como hacían los salinas de América del Norte o los galoma del Pacífico.

O incluso ha sido bastante frecuente que algunos pueblos, como los ododop o los mbai en África, utilizar los nombres generados por otras divisiones, 7 = 4 + 3 y 9 = 5 + 4.

Referencias:

Georges Ifrah, Historia universal de las cifras, Espasa Calpe, 2002.

Jamie Uys, Los dioses deben de estar locos, Sudáfrica, Botswana, 1980. Escena de la botella…

Survival (web page), los bosquimanos

San people (wikipedia)

Graham Flegg, Numbers through the ages, Macmillan, Open University, 1989.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica