La editorial puntodepapel, cuyo lema es “aprender no es un juego, pero jugando se aprende” acaba de publicar sus últimos libros, entre los que se encuentran “Buscando a LO”, “Paulhexaedro”, “Theresio”, “Fantasmilla”, o “A infinito”, del que vamos a hablar en esta entrada, en los cuales se entremezclan las matemáticas, la literatura y el arte.

El libro “A infinito”, de María Teresa Navarro, nos invita a jugar y reflexionar sobre el infinito en clave de humor. La autora lanza 38 ingeniosas preguntas, que nos recuerdan a las greguerías de Ramón Gómez de la Serna (1888-1963), alrededor de la idea de infinito. Aquí tenéis una muestra.
“¿Cuál es el aforo de infinito? ¿Quién controla si se ha superado?”
“Un quinto de infinito ¿debe de servirse bien frío? ¿Y con tapa?”
“Las cosas que tienden a infinito ¿se secan antes? ¿hay que alargar mucho el brazo para recogerlas?”
“Si vivo infinito ¿se refiere a la duración o a la intensidad?”
Tras disfrutar de la lectura de esta maravillosa obra, tomé la decisión de dedicar la siguiente entrada del Cuaderno de Cultura Científica, que es la que estás leyendo, a un sencillo aspecto de este concepto matemático.
El infinito, al igual que otros temas matemáticos, o científicos, que encierran algún tipo de misterio, que no podemos atrapar del todo en nuestra mente, que nos cuesta entender al cien por cien o que incluso están relacionados con propiedades que van contra la lógica común, como es también el caso de la cuarta dimensión (véase el libro “La cuarta dimensión” publicado por RBA dentro de la colección “El mundo es matemático”) o de las geometrías no euclídeas, ha despertado el interés de muchas personas en nuestra sociedad, y en particular, el de los artistas, quienes lo han incluido en sus obras.
El infinito es un concepto que podemos entender, pero que de alguna manera se nos escapa, no podemos atraparlo completamente. Un sencillo ejemplo para ilustrarlo serían los números naturales (1, 2, 3, 4,…). Todo el mundo entiende, hasta los niños y niñas (aunque no sin sorpresa), que los números naturales son infinitos (“Aita, ¿de verdad que los números son infinitos, que no se acaban nunca?” preguntaba mi hijo). Para cualquier número que se nos ocurra, por muy grande que sea (por ejemplo, el Asankhyeya, 10140, que era el número más grande según la religión budista; el número de Skewes, , que durante un tiempo fue el número más grande que aparecía en una demostración matemática; o el número Leviatán, que es (10666)! –donde el signo de exclamación “!” nos denota la operación factorial, es decir, la multiplicación desde el 1 hasta el número indicado, así 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720-, un número incalculable del que solo se puede tener pequeños trozos de información, como nos explica Pickover en su libro “El prodigio de los números”), siempre existe otro mayor, basta con sumarle el uno.
Si nos pusiésemos a contar, o a escribir, números sin parar a lo largo de toda nuestra vida, nos moriríamos, por supuesto, antes de llegar a infinito, puesto que nuestra vida sí es finita. Sobre estas ideas, el infinito, el paso del tiempo y nuestra mortalidad, son sobre las que trabajaba el artista conceptual francés, de origen polaco, Roman Opalka (1931-2011) en su singular obra “1965 / 1 – ”. Podéis leer el obituario que realizó Marta Macho en agosto de 2011 en ZTFNews, Roman Opalka, el pintor de los números.

Roman Opalka convirtió ese pensamiento conceptual sobre lo inalcanzable del infinito, y en particular la sencilla cuestión asociada de cuál es el número más grande al que llegaríamos si pasáramos toda nuestra vida (adulta) contando, y que pone en evidencia el paso del tiempo y lo efímero de nuestra existencia, en una realidad artística. Fue un artista atrevido, capaz de entender la importancia de una obra que para reflejar el paso del tiempo, e intentar evidenciar lo inalcanzable del infinito, requería de toda una vida. En mi opinión, esta es una obra de arte sublime, atrevida, inspiradora y de una fuerza desgarradora.

Un día del año 1965, en Varsovia, en la esquina superior izquierda de un lienzo totalmente negro colocó el número 1, al que le siguieron a su derecha el 2, después el 3, y luego todos los demás números, en orden creciente. El 6 de agosto de 2011, cuando falleció Roman Opalka, el último número que había pintado era el 5.607.249. Habían pasado 46 años y 233 “detalles”, que es como él llamaba a cada uno de los cuadros, puesto que la obra “1965 / 1 – ” era el conjunto de todos los lienzos en los que pintó números desde aquel día de 1965 hasta su muerte. Los lienzos eran de 196 x 135 centímetros. Los números los pintaba con una grafía sencilla, en color blanco, con un pincel número cero sobre un lienzo negro al principio, que pasaría al gris en 1968 y que al alcanzar el número un millón, en 1972, empezaría a aclarar introduciendo un 1% más de blanco, hasta el punto que a partir de 2008 prácticamente pintaba números blancos sobre un fondo blanco.
Pintó sobre el infinito (o la imposibilidad de alcanzarlo) y el paso del tiempo. En palabras del propio Opalka… “All my work is a single thing, the description from number one to infinity. A single thing, a single life” (“todo mi trabajo es una única cosa, la descripción desde el número uno al infinito. Una única cosa, una única vida”; aunque la palabra “single” la podemos traducir como “única”, pero también como “sencilla”) y “the problem is that we are, and are about not to be” (“El problema es que somos, y estamos a punto de no ser”).

Pero, volvamos a la sencilla pregunta ¿cuál es el número más grande al que llegaríamos si pasáramos toda nuestra vida (adulta) contando?, y tratemos de estimar cual sería ese número más grande al que podríamos llegar.
Realicemos una primera estimación rápida. Supongamos que esto es un trabajo que realiza una persona a lo largo de su vida laboral, por ejemplo, desde su juventud con 20 años hasta la jubilación con 65 años, en total, 45 años. El promedio de horas trabajadas al año en los países de la OCDE fue de 1.765 en 2.013 (en España son 1.686, en Alemania 1.397 o en Polonia 1.929). Y consideremos que de media se tardan 9 segundos en escribir un número (los primeros se escribirán más rápido, los siguientes con más cifras se tardará más, pero además hay que tener en cuenta el cansancio de una jornada laboral de unas 7 horas diarias). Entonces, podemos estimar que la cantidad de números que se puede escribir a lo largo de una vida laboral es
De nuevo, con esta estimación el número que se podría alcanzar es 31.770.000. Lo primero que llamó mi atención la primera vez que hice una estimación de este tipo, creo que por la pregunta de un periodista científico, es que el número era más pequeño de lo que yo imaginaba inicialmente. Lo cual ponía aún más de manifiesto lo efímero de nuestra existencia. Por otra parte, Roman Opalka realmente había trabajado mucho en su obra “1965 / 1 – ” puesto que había alcanzado el número 5.607.249, algo menos de la quinta parte de la estimación realizada.
Pero sigamos un poco más con la estimación de la cantidad de números que se pueden escribir a lo largo de una vida. El tiempo que se tarda en escribir un número de una sola cifra no es lo mismo que el que se tarda en escribir uno de 7 cifras, como los últimos que escribió Opalka. Por este motivo, vamos a rehacer la estimación teniendo en cuenta este hecho.
Para empezar, vamos a calcular la cantidad de números que tienen un número fijo de cifras. Así,
* con 1 cifra: del 1 al 9, hay 10 – 1 = 9 números,
* con 2 cifras: del 10 al 99, hay 100 – 10 = 90 números,
* con 3 cifras: del 100 al 999, hay 1000 – 100 = 900 números,
* en general, con n cifras, hay 10n – 10n-1 = 9 x 10n-1 números.
Supongamos, por otra parte, que el tiempo que utilizamos para escribir una cifra, y empezar a escribir la siguiente, es de un segundo (esta estimación es un poco burda, ya que el cansancio de una persona escribiendo números durante siete horas hará mella en la velocidad de escritura, pero mantengamos esa velocidad de un segundo, como si nuestro escribano fuese un robot al que no le afecta el cansancio), entonces el tiempo necesario para escribir todos los números que tengan hasta n cifras es
teniendo en cuenta que para ,
En consecuencia, ¿cuánto se tardará en segundos en escribir por ejemplo todos los números que tengan hasta 8 cifras?
En el caso de un robot, al que no le afectaría ni el cansancio, ni los horarios de una jornada laboral, y que escribiese ininterrumpidamente a una velocidad de una cifra por segundo, tardaría 25 años en escribir todos los números de 1 al 99.999.999.
Pero si volvemos a la estimación de una persona que escribe durante su jornada laboral (aún a una velocidad de una cifra por segundo) tardaría más de 124 años, lo que por desgracia supera nuestras expectativas de vida. Por lo tanto, una persona sola no podría llegar a escribir hasta el 99.999.999 (como ya sabíamos por nuestra primera estimación).
Por lo tanto, planteémonos cuánto tiempo necesitaría esa persona para escribir todos los números hasta 7 cifras, y luego cuántos números de 8 cifras podría escribir con el tiempo que le resta de vida laboral. Hasta las 7 cifras tardaría en segundos
o lo que es lo mismo, 10,84 años. En consecuencia, le quedarían 45 – 10,84 = 34,16 años para escribir números de 8 cifras. Como para cada número de 8 cifras se tardan 8 segundos y tendría 34,16 x 1.765 x 3.600 = 217.052.640 segundos, lo que equivalen a 27.131.580 números de 8 cifras. El primer número de 8 cifras es el 10.000.000, entonces número 37.131.579.
Pero volvamos a darle otra vuelta. Ya hemos comentado que para una persona mantener durante toda una jornada laboral (una de siete horas al día) el ritmo de una cifra por segundo es imposible, por lo que vamos a estimar una velocidad más lenta, y realista, y a rehacer los últimos cálculos.
Estimemos que durante las tres primeras horas de la jornada laboral (de siete horas), la persona que está contratada para escribir los números puede mantener la velocidad de una cifra por segundo, que durante las dos siguientes horas escribirá a una velocidad de una cifra cada dos segundos, mientras que las dos últimas horas necesitará tres segundos. La estimación sigue siendo generosa puesto que la persona que escribe parará de vez en cuando con dolores en la mano, para descansar un momento o por algún otro motivo. En total, en una jornada laboral de siete horas, que tiene 25.200 segundos, se podrían escribir 16.800 cifras, es decir, se necesitan 1,5 segundos para escribir cada cifra.
Por lo tanto, ahora el tiempo estimado que se necesita para escribir todos los números que tengan hasta 7 cifras es 16,26 años (10,84 x 1,5). Para escribir números de 8 cifras quedarán 45 – 16,26 = 28,74 años. Es decir, 28,74 x 1.765 x 3.600 = 182.613.960 segundos, pero para cada número de 8 cifras se necesitan 12 segundos (8 x 1,5), entonces se pueden escribir en ese tiempo restante, 15.217.830 números de 8 cifras. De nuevo, como el primer número de 8 cifras es el 10.000.000, entonces la persona encargada de escribir números llegaría al número 25.217.829.

Vamos a terminar esta entrada del Cuaderno de Cultura Científica, volviendo a ver el infinito en clave de humor, con el poema “Extracto del cuaderno de ejercicios escolares de Alicia (Operaciones con infinitos)” de José Florencio Martínez, recogido en “oetas, primera antología de poesía con matemáticas” de Jesús Malia…
1) ¿Pueden sumarse 17 infinitos?
2) ¿Cuál es la raíz cuadrada de 3 infinitos y 1/2 de cajas de bombones?
3) Si a 1 infinito de dioses le sustraemos 5 infinitos de dioses, ¿nos quedan -4 infinitos?
4) ¿Cuántos infinitos juntos de pulgas pueden correr en un caballo de luz?
5) ¿Es lo mismo una mariposa infinita que un número de mariposas sin fin?
6) Si la circunferencia es una forma infinita, ¿cuántos in¬finitos recorren las dos ruedas de una bicicleta persi¬guiendo la vaca perdida de Buster Keaton en un prado sin lindes?
7) A cero euros el infinito, ¿cuánto cuesta una infinidad de ceros?
8) Si suponemos que el resultado del problema anterior es cero, ¿estaba este cero incluido en el infinito de la infinitud en cuestión?
Bibliografía
1.- María Teresa Navarro, A Infinito, editorial puntodepapel, 2014.
2.- Raúl Ibáñez, La cuarta dimensión, ¿es nuestro universo la sombra de otro?, RBA, 2010.
3.- Clifford A. Pickover, El prodigio de los números, Ma non troppo, 2002.
4.- Nacho Nemeses, Roman Opalka, pintor de la infinitud, necrológica de El País, 13 de agosto de 2011.
5.- Marta Macho, Roman Opalka, el pintor de los números, ZTFNews, 2011
6.- Raúl Ibáñez, Infinitos infinitos (primera parte), divulgamat, 2012
7.- Raúl Ibáñez, Infinitos infinitos (segunda parte), divulgamat, 2012
8.- Jesús Malia (director de la colección pi de poesía), oetas, primera antología de poesía con matemáticas, Amargord, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Nota editorial: este artículo se ha corregido posteriormente a su publicación para subsanar un error en la fórmula para calcular el tiempo necesario para escribir un número de n cifras, lo que ha llevado a modificar algunas de las que aparecen a continuación de dicha fórmula. Estos cambios no modifican sustancialmente el contenido del texto.
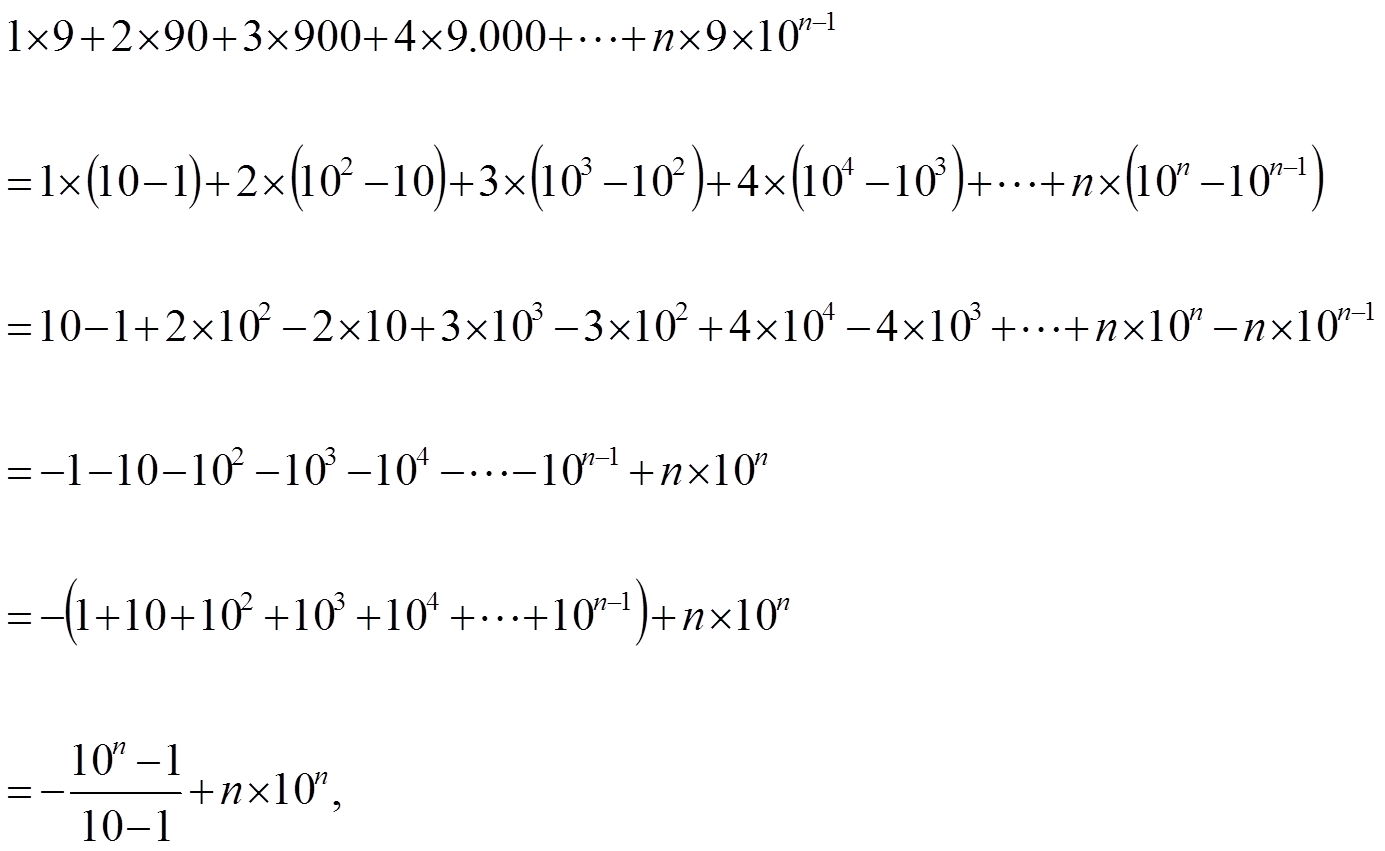
A infinito
[…] A infinito […]
Manuel Castro
Buenas, no querría pasar por estajanovista ni nada parecido, pero donde dice “Por otra parte, Roman Opalka realmente había trabajado mucho en su obra…” ¿no debería de haber una negación?
Aun teniendo en cuenta que comenzó con 34 años y terminó con 80, si hubiese trabajado las horas que se estiman para un trabajador (1765), me sale a un número escrito cada 52 segundos o, lo que es lo mismo, 15 cifras cada 13 minutos. Cierto que al acabar el buen hombre tenía ya la friolera de 80 años, pero incluso así parece una cifra pobre. Incluso suponiendo, que no parece el caso, que el señor Opalka hubiese decidido jubilarse a los 65, dando por finalizada su obra y dedicando sus últimos 15 años a contemplarla, habría escrito números a un promedio de una cifra cada 35 segundos, apenas dos cifras por minuto.
NOTA: Todo esto de aquí arriba es exclusivamente producto de mi problema patológico con los números, el artículo me parece fascinante.
Raúl Ibáñez
Querido Manuel,
Muchísimas gracias por tu comentario. Me alegro mucho de que el artículo te parezca «fascinante». Gracias.
En parte tienes razón, pero hemos de tener en cuenta que Roman Opalka no era una persona contratada para escribir números durante cada jornada laboral, como en la estimación que yo hago, sino un artista… con sus viajes, sus estudios, sus reuniones, su arte, quizás conferencias, etc… y realmente, desde esta perspectiva, dedicó bastante tiempo diario a trabajar en el proyecto…. si bien es cierto que era SU proyecto vital…
Gracias de nuevo por tus comentarios,
Un fuerte abrazo, Raúl.
Artículos sobre “a infinito” | Punto de Papel Editorial de libros para niños
[…] Raúl Ibáñez (Premio COSCE a la difusión de la ciencia 2011) escribe sobre el libro “a infinito” de María Teresa Navarro, recientemente publicado por puntodepapel, en el CUADERNO DE CULTURA CIENTÍFICA. […]
Artistas que miran a las matemáticas – Cuaderno de Cultura Científica
[…] con el teorema de Pitágoras (en la entrada Cultura pitagórica: arte), el infinito (en A infinito), la sucesión de Fibonacci (Póngame media docena de fibonaccis), los cuadrados latinos (Cuadrados […]