En esta anotación vamos a describir un ejemplo de una red de carreteras en la que una teórica mejora produce, sorprendentemente, que los tiempos de recorrido de los vehículos aumenten.
El diagrama 1 representa una red de carreteras en la que las vías secundarias se simbolizan en amarillo y las autovías en rojo.
La velocidad del tráfico en los tramos de A a X y Y a B –las carreteras secundarias– depende fuertemente de la cantidad de vehículos que circulan por ellos; si T es el número de automóviles transitando, se sabe que cada viajero necesita t=T/100 minutos para realizar el recorrido completo.
Los trayectos de A a Y y de X a B requieren, cada uno de ellos, un tiempo constante de 45 minutos: son vías rápidas en las que el tráfico es siempre fluido, independientemente del número de vehículos circulando.
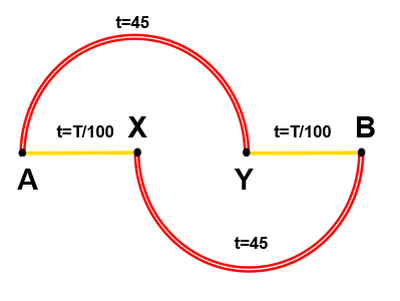
Supongamos que 4000 conductores quieren viajar desde A hasta B. Las rutas por el norte (de A a Y y de Y a B) y por el sur (de A a X y de X a B) son igualmente eficientes, por lo que los viajeros se dividirán –si no intermedia ningún dato adicional– en dos grupos, y llegarán al final de su trayecto en 2000/100 + 45 = 65 minutos.
Imaginemos ahora que los responsables de tráfico, intentando reducir los tiempos de los viajes, agregan un acceso directo entre X e Y, cuyo recorrido precisa sólo 1 minuto (ver diagrama 2). ¿Cómo razonará ahora un viajero cualquiera? Tomará la ruta de A a X ya que, en el peor de los casos –si los demás argumentan de la misma manera– tardará 4000/100 = 40 minutos en llegar de A a X, en lugar de los 45 minutos que invertía con la primera ruta. Tras 1 minuto para llegar de X a Y, de nuevo en el peor de los casos, necesitará 4000/100 = 40 minutos para llegar de Y a B.
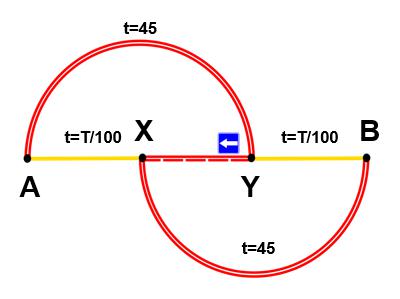
Es decir, el viaje le llevará 4000/100 + 1+ 4000/100 = 81 minutos… ¡16 minutos más que al principio, antes ‘de las mejoras’!
Ningún conductor –individualmente– tiene ningún incentivo para cambiar su manera de razonar y su comportamiento ulterior: de hecho, si todos los vehículos pudieran ponerse de algún modo de acuerdo para no usar el acceso directo recién añadido, todos reducirían su tiempo de viaje. Pero, sin una manera de coordinarlo, la ‘supuesta mejora’ sólo consigue desplazamientos más largos…
Este principio fue descubierto por el matemático Dietrich Braess (1938-) en 1968 y se conoce como la paradoja Braess.
Nota: Las imágenes están modificadas a partir de las que aparecen en Wikipedia
Más información:
- Braess’ Paradox, Futility Closet
- Wikipedia
- A Paradox on Traffic Networks, página de Dietrich Braess
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
Alfonso de la Fuente Ruiz
Interesante elección de tema. Incluyo algunas referencias adicionales sobre el asunto de la paradoja de Braess en problemas de congestión sobre grafos, incluyendo enlace a simulación interactiva, en el enlace adjunto: https://twitter.com/alfonsofr/status/715602738764201984
Marta Macho Stadler
Muchas gracias, ¡muy interesante!
Redes de carreteras y atascos: la paradoja de B…
[…] En esta anotación vamos a describir un ejemplo de una red de carreteras en la que una teórica mejora produce, sorprendentemente, que los tiempos de recorrido de los vehículos aumenten. […]
Hitos en la red #113 – Naukas
[…] real tenemos Simulación numérica de la fisión del plutonio-240 por Francisco R. Villatoro y Redes de carreteras y atascos: la paradoja de Braess de Marta […]
Hitos en la red #113 | NUEVAREGION.COM paz y no violencia, actualidad, Rosario San Lorenzo
[…] real tenemos Simulación numérica de la fisión del plutonio-240 por Francisco R. Villatoro y Redes de carreteras y atascos: la paradoja de Braess de Marta […]
La paradoja de Braess y las redes de carreteras | Ingeniería en la Red
[…] Redes de carreteras y atascos: la paradoja de Braess es un post de Cuaderno de Cultura Científica, de la Cátedra de Cultura Científica de la UPV/EHU, escrito por Marta Macho Stadler (a.k.a. @MartaMachoS) donde describe el principio que el matemático alemán Dietrich Braess en 1968 formuló donde ante la construcción una nueva vía en una red, o aumento de la capacidad de la misma, se podía producir un aumento de los tiempos de viaje. Un ejemplo real de la paradoja de Braess se constató en Nueva York en 1990 al cerrarse la Avenida 42 en Manhattan mejoró el tráfico y se pasó a una situación menos congestionada; o el aumento en China de su red de autovías, que pasó de 16.300 km en el año 2000 a los 70.000 km en 2010 produciéndose un aumento de 25 minutos de los tiempos medios de desplazamientos al trabajo en Beijing. […]
¿Añadir más carriles mejora el tráfico?. No siempre: Paradoja de Braess. | Blog de Jose Antonio Martin
[…] Redes de carreteras y atascos: la paradoja de Braess […]