Desde que el matemático suizo Leonhard Euler (1707-1783) introdujera en 1735 la teoría de grafos para resolver el famoso problema de los Puentes de Königsberg, esta teoría matemática ha demostrado ser una herramienta muy potente en diferentes ramas de la ciencia, la tecnología, e incluso las ciencias sociales.

La teoría de grafos es una teoría que sorprende por su sencillez inicial (ya que un grafo está formado simplemente por puntos –llamados vértices del grafo- y líneas que unen algunos de esos puntos –llamadas aristas del grafo-), por su versatilidad, así como por su fuerza para resolver problemas de lo más variado. Es precisamente su sencillez lo que hace que puedan utilizarse para crear modelos matemáticos en temas de lo más dispares.

La teoría de grafos, como decíamos, tiene muchas aplicaciones. Por ejemplo, las redes de ordenadores, o Internet, pueden representarse como un grafo y el estudio de la topología de las mismas ofrece información muy útil de su estructura y funcionamiento. Otra aplicación de la teoría de grafos en Internet es Google y su algoritmo PageRank, que clasifica las páginas web dándoles un orden de importancia, para lo cual los grafos han sido esenciales. En el estudio de las redes sociales se utiliza claramente la teoría de grafos, en epidemiología o propagación de enfermedades, en la difusión de innovaciones, en el análisis de impactos políticos, o incluso en la difusión de información, opiniones o rumores. Se utiliza también en cuestiones de transporte público, el diseño de recorridos óptimos en el reparto de mercancías, el diseño de rutas comerciales, y temas similares. La teoría de grafos se aplica claramente en las redes de telefonía y otras comunicaciones. Pero tiene también aplicación en muchos otros campos, como en temas de planificación de proyectos, en ingeniería eléctrica, en cristalografía, en estadística, en probabilidad, en lingüística, en genética o en geografía.

Pero también se utilizan los grafos en el análisis y resolución de los juegos y retos de ingenio. En esta entrada del Cuaderno de Cultura Científica vamos a mostrar un sencillo ejemplo de resolución de un problema de ingenio mediante el uso de un simple grafo (en este caso dirigido, es decir, las aristas tienen dirección). Es el problema de los tres caballeros y los tres criados.

Este es uno de esos típicos problemas de ingenio que consisten en una serie de personajes que tienen que cruzar el río con una barca y bajo ciertas condiciones, por ejemplo, el lobo, la cabra y la berza, o los maridos celosos. La primera vez que aparece publicado el problema concreto de los tres caballeros y los tres criados es en el libro Rational Amusements for Winter Evenings (1821) de John Jackson. Este reto también se suele presentar bajo la fórmula de los tres caníbales y los tres misioneros.

El problema dice lo siguiente:

Tres señores y tres criados deben de cruzar el río en una barca que solo permite que viajen dos personas. Solo hay un problema, los caballeros tienen motivos para sospechar que los sirvientes han conspirado entre ellos para robar a los señores y matarles. Por lo tanto, los caballeros son conscientes de que en ningún momento puede haber más criados que señores en alguna de las orillas, puesto que les matarían. ¿Cómo podrán cruzar el río?

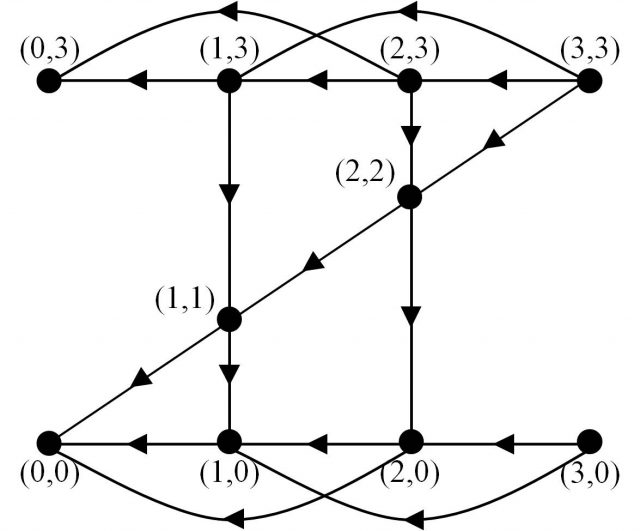
A continuación, vamos a asociar un grafo a este problema. Si c es el número de criados que hay en la primera orilla, y s el de señores, entonces un par (c, s) describe la situación en cada momento en la primera orilla, y por lo tanto, también en la segunda. La situación inicial sería (3,3) y la final (0,0). En total hay 16 posibles estados, pares de números, pero algunos no son posibles por las condiciones del problema, como (0,1), (0,2), (1,2), (2,1), (3,1) y (3,2), en estos casos los criados superan a los señores en alguna de las dos orillas. El resto de pares, que sí son posibles, los representamos en el plano cartesiano, y van a ser los vértices de nuestro grafo.

Ahora unimos esos vértices con aristas dirigidas, de forma que una arista dirigida que une dos posiciones, quiere decir que al cruzar la barca de la primera orilla a la segunda se pasa de la primera situación a la segunda, y por lo tanto, la dirección opuesta a la marcada representará a la barca pasando de la segunda orilla a la primera.

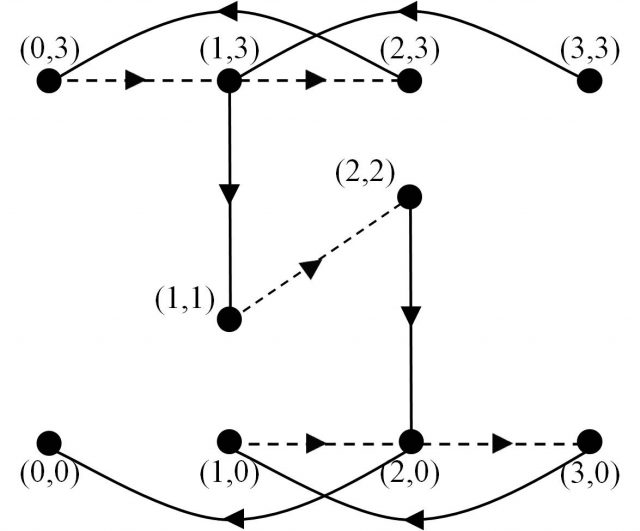
Entonces, la solución consiste en encontrar un camino, en el grafo dirigido, que empiece en el (3,3) y termine en el (0,0), alternando aristas en el sentido positivo (el marcado en el grafo) y en sentido negativo (el contrario al marcado), representando las idas y venidas de la barca. Una solución se muestra en la imagen (las aristas con línea discontinua son aquellas en las que se viaja de la segunda orilla a la primera, es decir, el sentido inverso al marcado en el grafo dirigido).

Existen muchos otros problemas de ingenio que se pueden resolver mediante grafos, por ejemplo, en el libro Las matemáticas de los juegos (2015) podéis encontrar más ejemplos.

Bibliografía

1.- Raúl Ibáñez, Las matemáticas de los juegos, RBA, 2015.

2.- Gary Chartrand, Introductory Graph Theory, Dover, 1985.

3.- D. Singmaster, Sources in Recreational Mathematics: An Annotated Bibliography, 8th preliminary edition, 2004.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica