Veíamos en la entrega anterior de esta serie que Kepler había mantenido una correspondencia muy interesante con Thomas Harriot y que, en el transcurso de ésta, Harriot le había mencionado a Kepler el problema del empaquetamiento de esferas. También mencionamos que Kepler llegó pronto a la conjetura de su nombre.

Como parte de este proceso, Kepler se dio cuenta que el empaquetamiento compacto de esferas en una sola capa da lugar a estructuras hexagonales que recuerdan a un panal de abeja. Esto le llevó a cuestionarse (y a buscar una respuesta satisfactoria) sobre la forma hexagonal de los copos de nieve en su tratado de 1611 Strena seu de nive sexangula (Un regalo de Año Nuevo de nieve hexagonal). Esto ya de por sí era bastante excepcional, ya que en aquella época no era común el conocimiento sobre la forma de los copos de nieve.

A título de ejemplo del conocimiento de la época tomemos el Historia de gentibus septentrionalibus (Historia de los pueblos del Norte) de Olof Månsson (latinizado Olaus Magnus), publicado en 1555. En él aparece una ilustración de los copos de nieve en la que es evidente que el autor, sueco por más señas, no es consciente de la forma hexagonal de los copos de nieve. Vemos que hay copos de nieve con forma de mano o de ojo o de media luna, por ejemplo.

Kepler llegó a la conclusión de que la forma de los cristales está relacionada con la geometría de los panales de abeja. Este empaquetamiento compacto del panal puede extenderse en las tres dimensiones de la misma forma en que los granos ocupan una granada. La elección de Kepler del copo de nieve (plano) para su explicación en vez de los cristales poliédricos de cuarzo que usó Cardano tiene la ventaja de que no le aplica la refutación de Scaligero (véase la IV entrega). Ni que decir tiene que este razonamiento, desde el punto de vista actual, no es válido: ni la molécula de agua es una esfera ni el empaquetamiento del cristal de agua de origen atmosférico puede ser llamado compacto de ninguna de las maneras. Sin embargo merece la pena detenernos un momento en él.

En el momento de componer De nive sexangula, Kepler ya era un convencido atomista y consideraba la materia como compuesta por átomos esféricos. Había evaluado dos maneras diferentes en las que las esferas se pueden empaquetar en dos dimensiones, cuadrada y hexagonal, comprobando que esta proporcionaba un empaquetamiento más compacto. La extensión de estos empaquetamientos a tres dimensiones llevaba, en el caso del cuadrado, a una disposición cúbica en el que cada esfera está rodeada por otras seis esferas (un empaquetamiento cúbico primitivo), mientras que la disposición hexagonal llevaba a un empaquetamiento más denso, en el que cada esfera tiene doce vecinos. Este es el empaquetamiento que el conjeturó que era el que tenía mayor densidad posible.

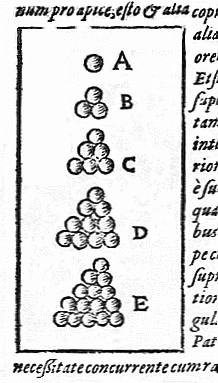
Al igual que Cardano y Kepler, Robert Hooke (del que ya hablamos en la II entrega) también creía que la naturaleza atómica de la materia también podría explicar las formas regulares de los cristales. A diferencia de los primeros, que se dedicaron casi en exclusiva a los hexágonos, Hooke también consideró otras formas y se dio cuenta de que el empaquetamiento compacto de esferas podría explicar toda clase de formas diferentes que se pueden encontrar en los cristales.

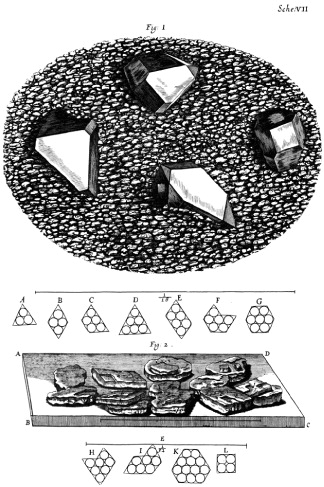
Hooke fue un paso más allá y dibujó en su Micrographia (1665) estudios detallados para intentar determinar cómo se empaquetan los átomos para dar lugar a las distintos cuerpos cristalinos. Su idea era observar detalladamente cristales, naturales y artificiales, para determinar todas las formas posibles, y después tratar de construirlas usando esferas. Fijémonos en que de aquí se sigue con naturalidad la idea de que sólo ciertos ángulos son posibles en los cristales; sin embargo, Hooke nunca dijo tal cosa de forma explícita, por lo que la ley de la constancia de los ángulos se atribuye a Steensen aunque su De solido es de 1669.

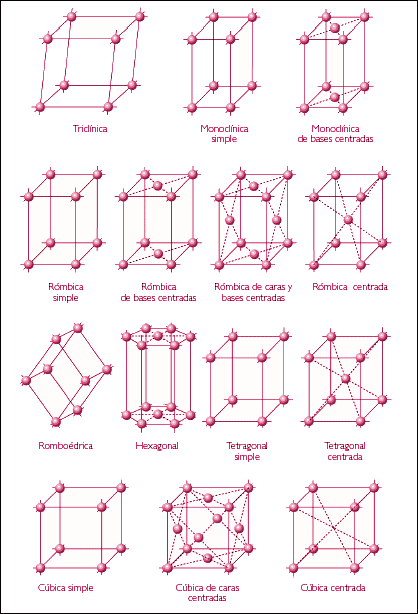
Hooke nunca completó su proyecto más ambicioso. De hecho se necesitaron 160 años de observaciones antes de poder intentar una construcción general de formas cristalinas. En 1826 Moritz Ludwig Frankenheim publicó Crystallonomische Aufsätze, su intento de sistematizar la mayoría de los cristales conocidos basándose en sus simetrías. Llegó a la conclusión de que sólo existían 32 combinaciones de operaciones de simetría. Hoy diríamos que sólo existen 32 grupos puntuales cristalográficos que definen 32 clases de cristales. Frankenheim no usó la definición de grupo (Galois, 1829) que no sería de uso generalizado hasta después de 1846.

En algunos textos el descubrimiento de los 32 grupos puntuales cristalográficos aparece atribuido a Johann F.C. Hessel, que lo realizó independientemente cuatro años después de Frankenheim, en 1830, aunque pasó desapercibido hasta que fue redescubierto por Ostwald en 1897; también aparecen atribuciones a Auguste Bravais (1848) y a Axel Gadolin (1867), dependiendo de si el texto es alemán, francés o ruso, respectivamente.

Este primer paso llevó a Frankenheim a considerar las maneras posibles que podría haber de ordenar puntos (átomos esféricos) periódicamente en el espacio euclidiano (hacemos esta puntualización porque los cuasicristales, que son cuasiperiódicos en el espacio euclidiano, son periódicos en espacios de al menos 5 dimensiones, pero este es otro tema). Llegó a la conclusión en 1845 (esta fecha es importante) de que sólo había 15 simetrías diferentes para una disposición periódica de puntos en el espacio, esto es, 15 redes cristalinas.

Frankenheim hizo todo el trabajo, pero otro se llevaría el mérito, una vez más. Como decíamos más arriba la teoría de grupos se popularizó entre los matemáticos a partir de 1846, un año después de la publicación de Frankenheim. En 1848, Auguste Bravais publica sus Études Cristallographiques en el que expone los hallazgos de Frankenheim pero hace notar matemáticamente que dos de las redes de Frankenheim son, de hecho, equivalentes, y que, por lo tanto, el número de redes elementales es 14. Desde entonces se las conoce como redes de Bravais, mientras que reto al amable lector a que busque alguna cita a Frankenheim en algún texto cristalográfico general.

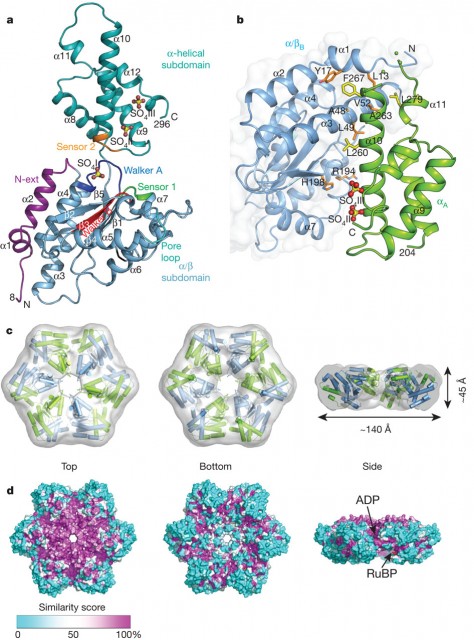
Así, Frankenheim (y Bravais) habían resuelto el problema de disponer puntos en el espacio. Pero, ¿qué pasa si lo que hay que distribuir espacialmente son moléculas que no tienen por qué tener una simetría propia? Esta es la pregunta que al final fue resuelta en 1891 por dos matemáticos que publicaron independientemente las definiciones de los 230 grupos espaciales cristalográficos (si se admite que las copias quirales son distintas; si no, 219), pero que colaboraron en la elaboración de estas ideas, Evgraf Stepánovich Fiodorov y Arthur Moritz Schönflies.

Si bien la forma de los cristales era un buen argumento a favor de la teoría atómica, y que la teoría atómica también era una buena base para las teorías cristalográficas, la oposición al atomismo persistía. El concepto había sido revitalizado a principios del siglo XIX por John Dalton, pero hasta el primer Congreso de Químicos en Karlsruhe (1860) no tuvo una especie de reconocimiento oficial. Con todo, muchos científicos abominaban de la teoría y lo siguieron haciendo hasta entrado el siglo XX. La verdad es que no se les puede acusar de cabezonería o falta de conocimiento, si acaso de rigor excesivo o de dejarse llevar por según qué corriente filosófica. En cualquier caso, las pruebas experimentales definitivas se encontrarían en el siglo XX: la radioactividad, la confirmación de la teoría de Einstein del movimiento browniano y, mire usted por donde, la difracción de los rayos X por los cristales.

Referencias generales sobre historia de la cristalografía:

[1] Wikipedia (enlazada en el texto)

[2] Cristalografía – CSIC

[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378

[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528

[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459

[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453

Este texto es una revisión del publicado en Experientia docet el 12 de diciembre de 2013

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance