Cuando esta mañana me he decidido a escribir una tercera entrega de esta serie de entradas del Cuaderno de Cultura Científica, Los números poéticos, sobre poemas con contenido o referencias matemáticas, tenía dos ideas en la cabeza. La primera era empezar esta entrada con la poeta estadounidense Emily Dickinson (1830-1886), de la que confieso que no había leído nada hasta hace poco tiempo, pero que es uno de los nombres claves de la historia de la poesía y de la literatura universal. La segunda era terminar con uno de los grandes poetas vascos, Gabriel Celaya (1911-1991), del cual sí había leído bastantes poemas, algunos de ellos relacionados con las matemáticas.

Si buscamos en cualquiera de las biografías publicadas sobre la escritora estadounidense Emily Dickinson, que son muchas, alguna relación de ella con las matemáticas, lo primero que llama la atención es que estudió durante 7 años, entre 1840 y 1847, en la Academia Amherst, de Massachusetts. La amplia educación que recibió en dicha institución incluía, en particular, una buena formación en matemáticas. Entre los textos que se utilizaban en las clases se mencionan la edición de John Playfair (1748-1819) de Los Elementos de Euclides, La introducción al álgebra de Jeremiah Day y “la Aritmética de Adam”, pero también textos de astronomía y lógica.

Por otra parte, su cuñada fue la escritora y poeta Susan H. Gilbert Dickinson (1830-1913), buena amiga desde la adolescencia y con quien mantuvo una importante relación epistolar. Susan Gilbert fue “matemática y profesora de matemáticas en Baltimore en 1851-52”. Y se encuentran referencias a las matemáticas en algunas de sus cartas, como en una de Emily a Susan de 1851 que dice “Te imagino muchas veces bajando al aula con un rollizo Teorema Binomial luchando en tus manos”.

Quizás las matemáticas no fueran la materia que más interesaba a la escritora, o incluso no se le dieran muy bien, pero lo cierto es que sí parece que a lo largo de su vida las matemáticas sí provocaron cierto interés y fascinación en ella, que motivaron la utilización de algunos términos e ideas matemáticas en sus poemas.

Empecemos con una sencilla aritmética de la mano de Dickinson, la negación de la más simple evidencia matemática, que uno más uno es dos. El poema clasificado con el número 769 según la clasificación de Thomas H. Johnson, en su obra The Complete Poems of Emily Dickinson (1960), y que aparece, por ejemplo, publicado en castellano en el libro Emily Dickinson. Poemas a la muerte (Selección, traducción y prólogo de Rubén Martín. Bartleby, Madrid, 2010), dice así:

Uno más Uno — es Uno —
El Dos — es una fórmula gastada —
Buena para enseñarla en las Escuelas —
pero Inferior como Elección —

La propia – Vida — o la Muerte —
o más aún la Eternidad —
serían — demasiado vastas
para que las comprenda nuestro Espíritu —

Otro de los conceptos matemáticos que utiliza en su poesía es el álgebra. Por ejemplo, en el poema 600 (de 1862), que podemos leer en el libro Emily Dickinson. Poemas (Selección y traducción de Silvina Ocampo y prólogo de J.L. Borges. Tusquets editores, Barcelona, 1985), y que dice así…

Antes me perturbaba —
pues yo fui una vez una niña —
conjeturar cómo un átomo — caía —
y sin embargo los cielos — no —

los cielos pesaban mucho más —
azules — y sólidos — permanecían —
sin un perno — que yo pudiera comprobar —
¿podrían los gigantes — comprender?

La vida presentó más grandes — problemas —
algunos guardaré — para resolver
hasta que el álgebra sea más fácil —
o más simplemente probado — arriba —

y luego también — ser comprendida —
qué dolor — me confundía —
por qué el cielo no se rompía —
y caía — azul — sobre mí —

El término “álgebra” también aparece en el poema 269 (que se recoge también en el libro Emily Dickinson. Poemas), escrito en 1861, y que incluye los versos “Tantas — gotas — de vital escarlata — / lidian con el alma/ lo mismo con el álgebra!”. Otro término matemático que aparece en algunos poemas es “logaritmo”, como en el poema 433 (también en el poemario anterior), que dice así “aunque yo fui a la escuela/ no me volví muy sabia/ nada me enseñó el globo/ tampoco el logaritmo”. O en el poema 728 que podría traducirse como algo así “Saciando mi hambre/ con mi diccionario/ el logaritmo –lo tenía yo- para la sed/ como un vino muy seco”.

En tres poemas menciona a las matemáticas. En el poema 1668, que podemos encontrar traducido en el libro Emily Dickinson. Poemas (Edición bilingüe de Margarita Ardanaz, Cátedra, 1987), se incluyen los versos “sé que es un signo/ de que el nuevo dilema esté/ más alejado de las matemáticas/ que de la eternidad”. En otro poema, el 88, se habla de “matemáticas quebradas”. En opinión de Thomas Johnson la poeta puede referirse a las matemáticas como “un sistema ‘quebrado’ en su incapacidad para demostrar sus [de Emily Dickinson] especulaciones”. La profesora de literatura de la Universidad de Harvard, Seo-Young Chu, en su artículo Dickinson and Mathematics, relaciona la expresión “matemáticas quebradas” con las fracciones.

Otros términos matemáticos aparecen en los poemas de Dickinson, “infinito”, “cifra”, “decimales”, … o “geometría”, como en el poema 359, que está recogido en el libro Emily Dickinson. Crónica de Plata (Selección y traducción de Manuel Villar Raso, Hiperión, 2001), que dice así…

La mejor brujería es Geometría
Para la muerte del mago —
Sus actos corrientes son proezas
Para el pensar humano.

Pero el concepto matemático que más menciona Emily Dickinson en su poesía es la “circunferencia”. En una carta al escritor y pastor de la Iglesia Unitaria Thomas Wentworth Higginson (1823-1911) le llega a escribir que “mi asunto [business] es la circunferencia”. Finalicemos con uno de esos “poemas de circunferencias”, el poema 802, que aparece en la selección de Margarita Ardanaz para Cátedra.

Da sensación de ser vasto el Tiempo, que si no fuera
Por una eternidad —
Temo que esta Circunferencia
Mi Finitud absorba —

De Su exclusión, quien se prepare
Por los Procesos del Tamaño
Para la Gran Visión
De Sus Diámetros —

En este poema, Emily Dickinson establece un cierto paralelismo entre la relación que existe entre la temporalidad “finitud” y la eternidad, y la relación de la circunferencia con “sus diámetros”. Esta relación, el cociente entre la circunferencia y el diámetro de la misma, es el importante número π, independientemente del tamaño de la circunferencia, “por los Procesos del Tamaño”.

Estos poemas relacionados con la circunferencia me han recordado dos poemas de la poeta extremeña Ada Salas (Cáceres, 1965), relacionados con el círculo y la esfera. El primero de ellos pertenece a su libro Lugar de la derrota (Hiperión, 2003), y describe la perfección del círculo, de su simétrica construcción.

Exactitud del círculo.
Perfecta equidistancia
en torno a un centro.
Aguja del compás que se desliza
y traza
la forma inexorable de la espera.

Por otra parte, en su libro Arte y memoria del inocente (Universidad de Extremadura, 1988), que obtuvo el Premio Juan Manuel Rozas, aparece este bello poema: “Vivir/ para limar los ángulos/ a las esferas”.

Y seguimos un poco más con poemas geométricos. El siguiente poema es de otra de las grandes poetas en lengua española, la poeta modernista argentina Alfonsina Storni (1892-1938). Es el poema Cuadrados y ángulos, perteneciente a su libro El dulce daño (1918), pero que yo he leído en el libro Alfonsina Storni. Antología mayor (Hiperion, 2005).

Casas enfiladas, casas enfiladas,
casas enfiladas.
Cuadrados, cuadrados, cuadrados.
Casas enfiladas.
Las gentes ya tienen el alma cuadrada,
ideas en fila
y ángulo en la espalda.
Yo misma he vertido ayer una lágrima,
Dios mío, cuadrada.

De una poeta modernista argentina pasamos a una poeta modernista estadounidense, Marianne Moore (1887-1972), que entre otras distinciones recibió el Premio Pulitzer de Poesía en 1952. El siguiente poema La icosaesfera está recogido en el libro Marianne Moore. Poesía completa (Lumen, 2010).

«En los setos vivos de Buckinghamshire
los pájaros anidan en la verde espesura sumergida,
tejen trocitos de cuerda, polilla, plumas y vilanos,

en parabólicas curvas concéntricas” y,
buscando la concavidad, dejan proezas esféricas de rara eficacia;]
mientras que, por falta de integración,

ávidos de la fortuna ajena,
tres fueron asesinados y diez cometieron perjurio,
seis murieron, dos se suicidaron y dos pagaron multas por los riesgos que corrieron.]

Pero entonces aparece la icosaesfera
donde por fin se consigue cortar acero con mínimo desperdicio,]
ya que veinte triángulos unidos envuelven una

pelota o una doble concha esférica
sin apenas recortes, tal es la limpieza geométrica
de un icosaedro. ¿Quieren explicarnos los ingenieros que la construyeron,]

o Mr. J. O. Jackson
cómo pudieron los egipcios levantar verticalmente setenta y ocho pies cúbicos de granito?]
Nos gustaría saber cómo lo hicieron.

Una poeta que también cuenta con algunos poemas relacionados, de alguna forma, con las matemáticas, es la poeta y filósofa española Chantal Maillard (Bruselas, 1951), quien, entre otros galardones, ha recibido el Premio Nacional de Poesía, en 2004, por la obra Matar a Platón. Con la intención de cambiar de tema, de volver a los números poéticos que han dado lugar a esta pequeña serie de entradas del cuaderno de Cultura Científica, he elegido un poema de Chantal Maillard, perteneciente al libro La herida en la lengua (Tusquets, 2015), que nos habla de la desconexión entre el número matemático, el número en abstracto, y su significado al contabilizar objetos, como puedan ser las victimas de una guerra o las casas destruidas en la misma.

Diez millones.
Un número.
Un número tan sólo
para diez
millones
de casas incendiadas
de cuerpos mutilados
de gritos
silenciados
uno
a
uno
en boca que arde y
no entiende.
1
0
0
0
0
0
0
0
siete
veces
el signo de la nada sobre
diez
millones
de historias
que nunca contará
la lengua de los otros.
Dos palabras.
Cuatro sílabas.
Un globo que soltamos
Al final de la fiesta.
La piñata que espera
el golpe de una mano
nunca
inocente.

Antes de terminar esta entrada con algunos poemas del poeta guipuzcoano Gabriel Celaya, me ha parecido interesante incluir el poema Aritmética (traducción libre que yo mismo he realizado), del escritor y poeta estadounidense Carl Sandburg (1878-1967), quien ganó tres premios Pulitzer, uno por su biografía de Abraham Lincoln y dos por su obra poética.

La aritmética es donde los números vuelan como palomas dentro y fuera de tu cabeza.

La aritmética te dice cuánto pierdes o ganas si sabes cuánto tenías antes de perder o ganar.

La aritmética es nueve cinco llueve con ahínco – o siete ocho chocolate en el bizcocho.

La aritmética es exprimir números de tu cabeza a tu mano, a tu lápiz, a tu papel hasta encontrar la respuesta.

La aritmética es donde la respuesta es correcta y todo es agradable y puedes mirar por la ventana y ver el cielo azul – o la respuesta es incorrecta y tienes que empezar todo de nuevo y volver a intentarlo y ver cómo sale bien esta vez.

Si tomas un número y lo duplicas y lo duplicas de nuevo y entonces lo duplicas unas pocas veces más, el número se hace cada vez más grande y es cada vez más elevado y sólo la aritmética puede decirte qué número se obtiene cuando decides parar de duplicar.

La aritmética es donde tienes que multiplicar – y llevas la tabla de multiplicar en la cabeza y esperemos que no la pierdas.

Si tienes dos galletas de animales, una buena y una mala, y te comes una y una cebra toda llena de rayas se come la otra, ¿cuántas galletas de animales tendrás si alguien te ofrece cinco seis siete y tú dices No no no y tú dices nes nes nes y tú dices neis neis neis?

Si le pides a tu madre un huevo frito para el desayuno y ella te da dos huevos fritos y tú te comes ambos, ¿quién es mejor en aritmética, tú o tu madre?

Como ya habíamos anunciado, vamos a terminar con Gabriel Celaya, uno de los representantes de la conocida como poesía social, fundador de la colección de poesía Norte, junto a la poeta Amparo Gastón (su Amparitxu), y Premio Nacional de Poesía en 1986. Si se realiza un repaso sobre el conjunto de su obra, por ejemplo, a través de los tres tomos de Gabriel Celaya. Poesías Completas (Visor, 2001), se observa un profundo interés por los temas científicos, no en vano Gabriel Celaya estudió Ingeniería Industrial. Por ejemplo, la física de partículas es el tema central del poemario Lírica de cámara (1969) o utiliza las funciones matemáticas como metáfora en su libro Función de Uno, Equis, Ene (1973), donde “Uno” es el individuo, “Ene” es el colectivo y “Equis”el universo que se rige por leyes no humanas. En estos libros Gabriel Celaya transmite su idea de que el mundo, el universo, funciona con leyes que nada tienen que ver con la subjetividad humana, con el individualismo, son leyes universales, más allá del “hombre”.

Además, en su libro Exploración de la poesía (Seix Barral, 1964) el poeta de Hernani compara la poesía con las matemáticas, “el poeta se parece al matemático, que ha creado una notación peculiar y ha derivado de ésta un idioma propio” y también, “el poeta da palabras combinadas, como el matemático, ecuaciones, que ni uno ni otro pueden explicar o decir mejor que con esas mismas palabras o ecuaciones”.

La poesía de este poeta comprometido está plagada de referencias matemáticas. Los números y operaciones aritméticas son frecuentes, como en uno de sus poemas de la época inicial en la que firmaba como Rafael Múgica, que dice así “Debajo del pino verde me niego a multiplicar. Y a sumar”, en el poema Apus o el ave del paraíso, de Objetos poéticos (1948), escribe “Verá que dos y dos/ en vez de sumarse,/ se abrazan (se matan)/ o cambian sus nombres”, en el poema La Rosa, de Movimientos elementales (1947), escribe de “un torrente loco de cifras arbitrarias: mil millones, cien ceros”, en Telegrama urgente, de Avisos de Juan de Leceta (1961), nombre con el que también firmó algunos de sus poemas, puede leerse “Las máquinas tiritan/ dando diente con diente, seca cifra con cifra./ Nueve, diez, mil millones/ de ceros con ombligo y con sombrero”, en El amor multiplicado, de Lo que faltaba (1967), la suma y la multiplicación están presentes en todo el poema, que empieza con la estrofa “Yo pregunté: «¿Dos y dos? »/ Me explicaron: «No son cuatro./ Es decir, en cierto modo,/ porque bien considerado…»”, que sigue con “Insistí: «¿Dos y dos, cuatro?»/ Respondieron «¿Dice seis?»/ –«Yo decía lo que digo»./ –«Podemos seguir sumando».”, y sigue con tres estrofas más hasta la última “–«Digo dos»./ –«Yo digo Dios»./ Dos por Dios, ¡qué confusión!/ Este amor, de aguante usted,/ es la multiplicación.”, en su poema Biografía, de La higa de Arbigorriya (1975), que está escrito en forma de normas que nos imponen a lo largo de la vida, en la estrofa de su etapa escolar escribe “Extraiga la raíz cuadrada de tres mil trescientos trece” o en el poema Total, cero, de Buenos días, Buenas noches (1978), menciona el número pi, “Y pensar/ que uno va, y luego se enfada/ con su chica por diez, doce,/ tres coma catorce dieciséis minutos de retraso/ a la hora de la cita”, por citar algunos ejemplos.

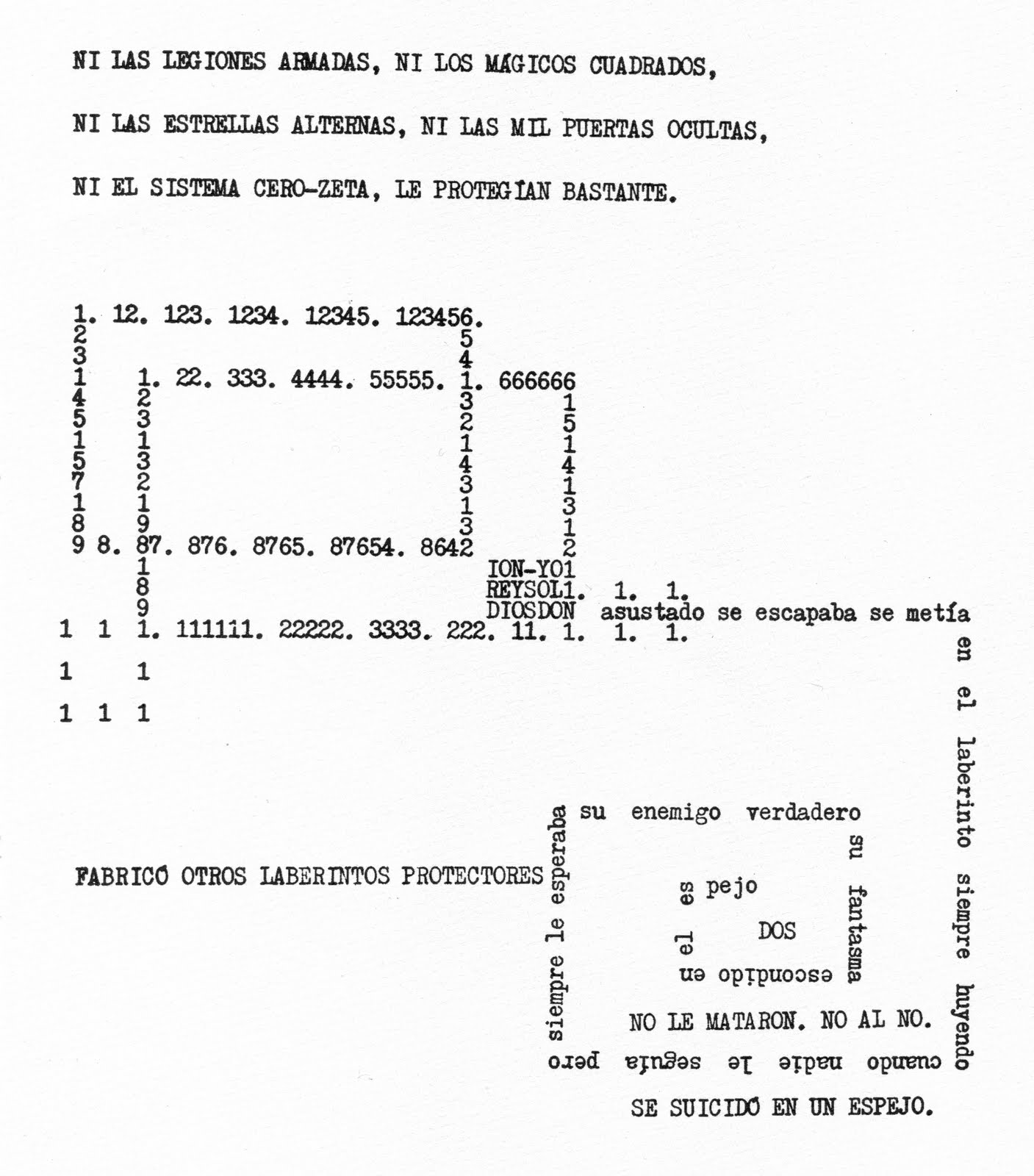
Aunque quizás el poema más conocido en este sentido sea el que vamos a mostrar a continuación, titulado Tablas de Multiplicar, perteneciente al poemario Ciento volando (1953), en el cual también se incluye el poema La máquina de calcular.

UNO por otro es el hombre
cualquiera como Dios manda
y ese salvar las distancias
que –mala cuenta– se cantan.

Dos por uno es la evidencia
que en un dos por tres tendrás.
Dos por cuatro, buen compás.
Dos por cinco, la sorpresa
del diez redondo y total.
¡Qué divino es, por humano,
el sistema decimal!

Cero por cero es la luz.
Cero por uno, el problema
(pues con el yo creo el tú).
Cero por dos, el amor.
También cero, mas en ¡oh!
(¡Oh!, que es un eco de yo).
Cero por tres… ¡Atención!
Debe haber algún error,
pues cuanto más multiplico
más repito: yo, yo, yo.

En varios poemas se alude a la “matemática Urania”. Recordemos que Urania era la musa de la astronomía, y también se la suele considerar la musa de las matemáticas.

También nos encontramos con algunos conceptos geométricos en los poemas de Gabriel Celaya, y como ejemplo su poema Así se escribe la ciencia (Homenaje a Kepler), de su poemario Espejos Transparentes (1968).

KEPLER miró llorando los cinco poliedros
encajados uno en otro, sistemáticos, perfectos,
en orden musical hasta la gran esfera.
Amó al dodecaedro, lloró al icosaedro
por sus inconsecuencias y sus complicaciones
adorables y raras, pero, ¡ay!, tan necesarias,
pues no cabe idear más sólidos perfectos
que los cinco sabidos, cuando hay tres dimensiones.
Pensó, mirando el cielo matemático, lejos,
que quizá le faltara una lágrima al miedo.
La lloró cristalina: depositó el silencio,
y aquel metapoliedro, geometría del sueño,
no pensable y a un tiempo normalmente correcto,
restableció sin ruido la paz del gran sistema.
No cabía, es sabido, según lo que decían,
más orden que el dictado. Mas él soñó: pensaba.
Eran más que razones: las razones ardían.
Estaba equivocado, mas los astros giraban.
Su sistema era sólo, según lo presentido,
el orden no pensado de un mundo enloquecido,
y él buscaba el defecto del bello teorema.
Lo claro coincidía de hecho con el espanto
y en la nada, la nada le besaba a lo exacto.

Y para terminar desearos… ¡¡Mucha matemática y poesía!!

Bibliografía

1.- Raúl Ibáñez, Los números poéticos, Cuaderno de Cultura Científica, 2018.

2.- Raúl Ibáñez, Los números poéticos (2), Cuaderno de Cultura Científica, 2018.

3.- Cynthia Griffin Wolff, Emily Dickinson, Knopf, 1986.

4.- Seo-Young Jennie Chu, Dickinson and Mathematics, The Emily Dickinson Journal, Volume 15, Number 1, p. 35-55, 2006.

5.- Lista de poemas (en inglés) de Emily Dickinson en Wikipedia

6.- Blog de poemas de Emily Dickinson

7.- Página web de Chantal Maillard

8.- Página web sobre Gabriel Celaya, de la Diputación Foral de Gipuzkoa

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica