Mi anterior entrada de la sección Matemoción del Cuaderno de Cultura Científica, titulada Imago mundi, 7 retratos del mundo, estaba dedicada a mostrar diferentes retratos del mundo, en concreto, 7 mapas diferentes del planeta Tierra. Bueno, en realidad, mostrábamos 7 formas diferentes de realizar mapamundis, a través de 7 proyecciones cartográficas (matemáticas) diferentes: la proyección cilíndrica conforme de Mercator, la proyección pseudo-cilíndrica isoareal de Mollweide, la proyección pseudo-cilíndrica isoareal de Eckert IV, la proyección isoareal interrumpida homolosena de Goode, la proyección convencional de Van der Grinten, la proyección central, que preserva los caminos más cortos, y la proyección estereográfica, que es conforme.

A la hora de realizar un mapa, la proyección cartográfica es la herramienta matemática que nos permite transformar la superficie terrestre, de forma esférica (geoide), en una superficie plana, aunque en el diseño del mapamundi intervienen muchos otros elementos, científicos, técnicos, artísticos, socio-políticos, etc. Por ejemplo, el mapa anterior, realizado con la proyección cilíndrica conforme de Mercator, está centrado en el meridiano de Greenwich, sin embargo, el siguiente mapa que mostramos está realizado con la misma proyección cartográfica, pero está centrado en el océano Pacífico, dejando Asia y Oceanía a la izquierda de la línea central y a América a la derecha.

Por otra parte, el primero de los “mapas con el sur arriba” modernos fue el diseñado en 1979 por el australiano Stuart McArthur, cansado de las continuas bromas sobre “down under” (que podemos traducir como “abajo del todo”), que era una forma coloquial de referirse a Australia y Nueva Zelanda. Es el mapa conocido como Mapa Correctivo Universal de McArthur, y aunque su gran aportación es situar el sur arriba, también está realizado con la proyección de Mercator. Por lo tanto, aunque solemos hablar del mapa de Mercator, esto es ambiguo y más bien deberíamos de hablar de mapas realizados con la proyección de Mercator.

Pero, continuemos mostrando diferentes retratos del mundo, realizados con nuevas proyecciones.

Retrato 1: la proyección rectangular o carta plana

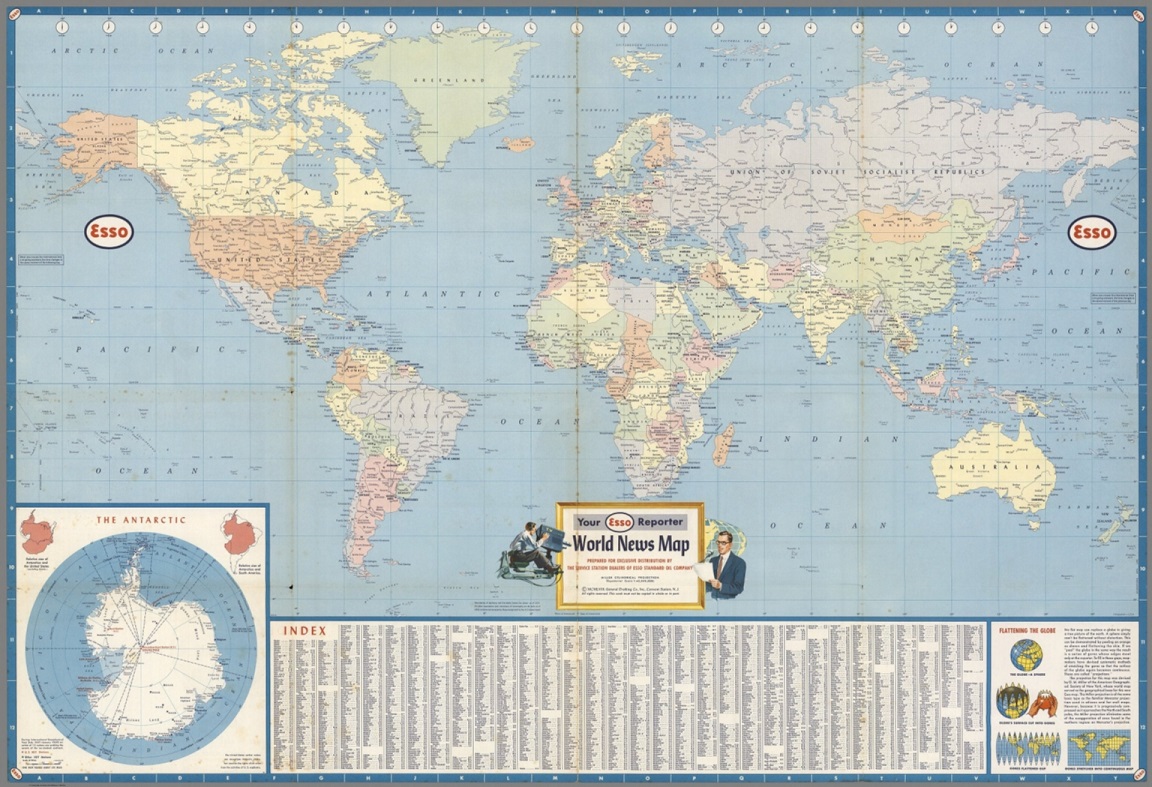
La proyección rectangular, también llamada equirectangular o carta plana, es la proyección cartográfica más sencilla, desde el punto de vista matemático, puesto que son la latitud y la longitud directamente las coordenadas cartesianas del plano. En esta proyección los meridianos y paralelos están igualmente espaciados, de manera que forman una red cuadrada.

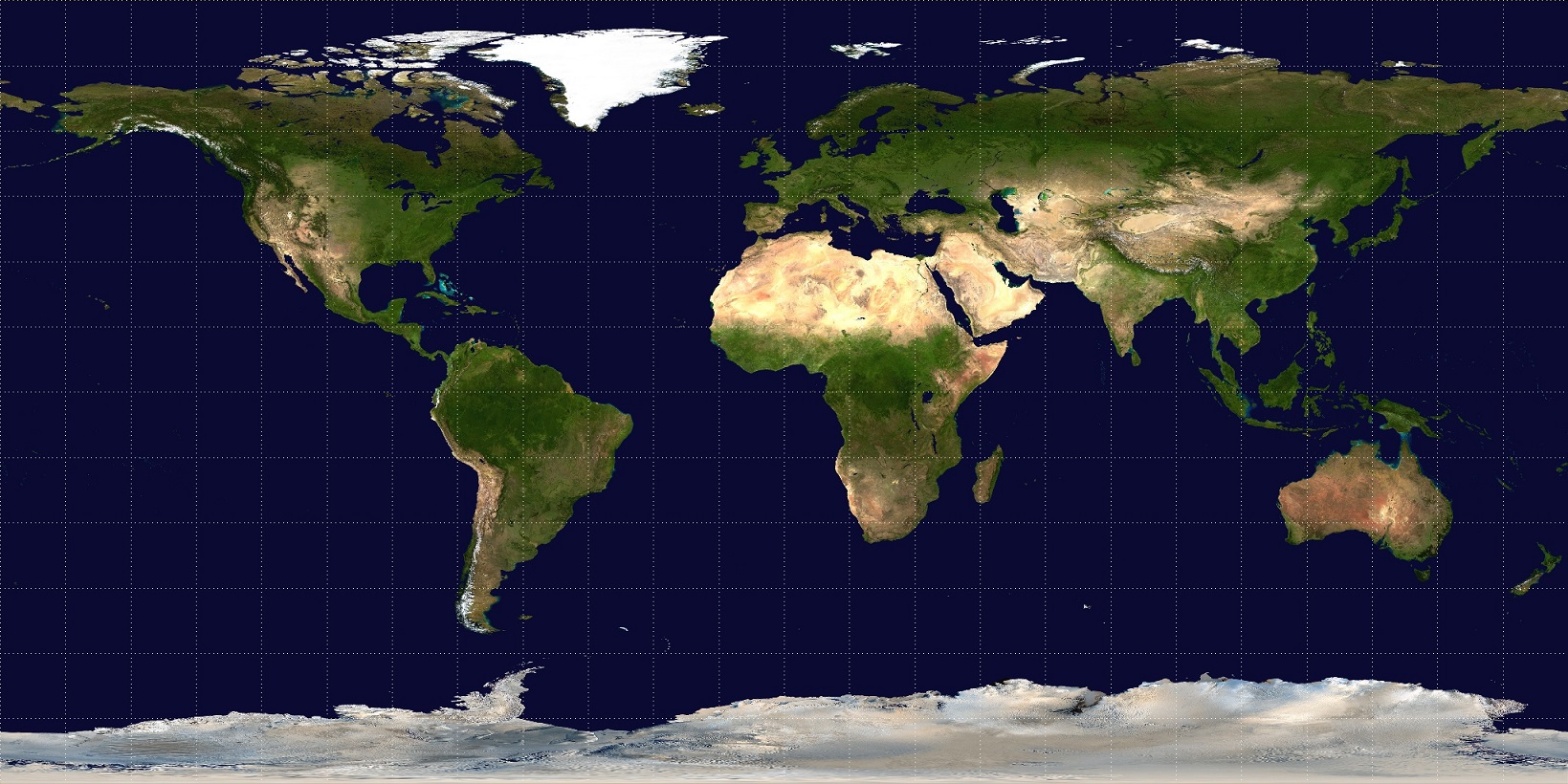
Esta proyección suele atribuirse al sabio griego Eratóstenes de Cirene (276-194 a.n.e.), aunque el astrónomo y matemático romano Claudio Ptolomeo (aprox. 90-170) cita al geógrafo fenicio Marino de Tiro (aprox. 60-130) como su inventor hacia el año 100. A partir de entonces fue ampliamente utilizada, en particular, para la navegación, debido a la sencillez de construcción. Suele utilizarse mucho para mapamundis sencillos. La USGS y otras agencias suelen utilizarlo para mapas índice, es decir, aquellos en los que se situan esquemáticamente los diferentes mapas incluidos en una serie o atlas, y en los que se indica la página o referencia de localización.

Se ha convertido en standard para programas informáticos para procesar mapas globales, por la correspondencia entre pixeles y su situación geográfica, como Celestia.

Retrato 2: la proyección cilíndrica de Miller

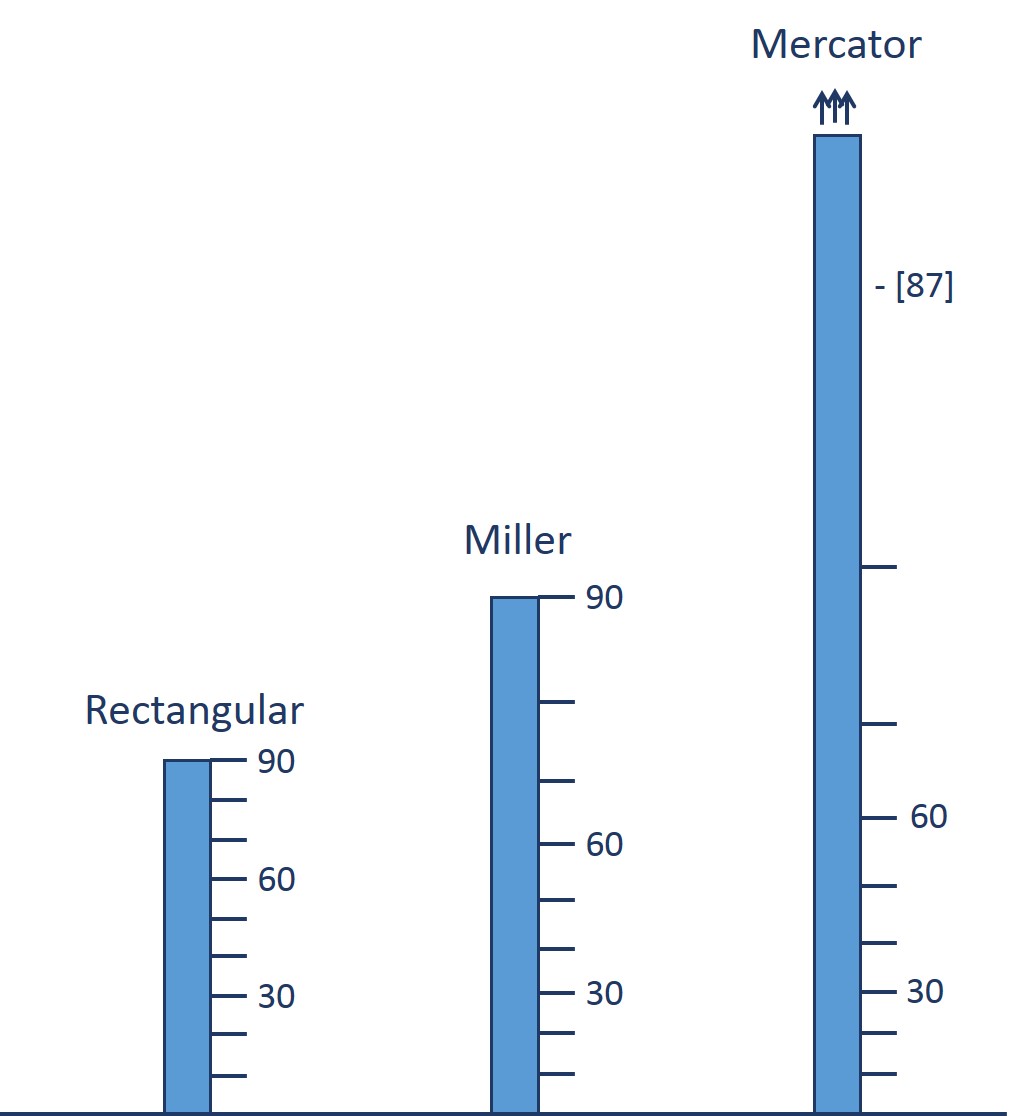
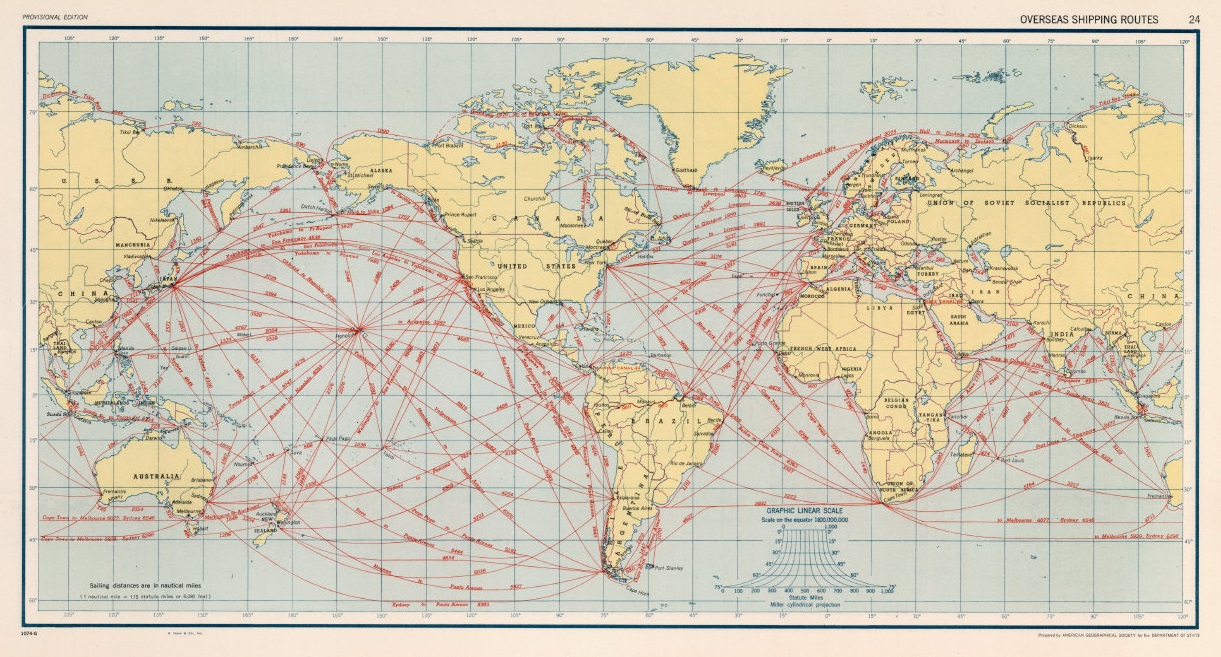
Esta proyección cartográfica fue diseñada por el cartógrafo escocés-americano Osborn Maitland Miller (1897-1979) en 1942, con el objetivo de crear un mapa que mantuviese la imagen del conocido mapa de Mercator, de sus familiares formas, pero sin tanta distorsión hacia los polos. En la proyección equirectangular, los paralelos están igualmente espaciados, mientras que en la proyección de Mercator, se van separando cada vez más, según vamos acercándonos a los polos, cerca de los cuales la separación es muy grande, y también la distorsión. Lo que hizo Miller fue comprimir la proyección de Mercator, en la dirección norte-sur, juntando más los paralelos, y por lo tanto, con menos distorsión en los polos.

Esta proyección cilíndrica no preserva ninguna propiedad métrica, ni ángulos, ni áreas, ni geodésicas (los caminos más cortos). Esta es una proyección bastante utilizada. El mapa del mundo Esso (imagen de abajo) fue la primera vez, 1942, en la que se utilizó esta proyección, despues el gobierno de EE.UU. empezó utilizarla, en 1943, en el Servicio de Mapas del Ejercito (mapa de arriba) y en la U.S. Geological Survey, y siguió utilizándose para mapas en atlas comerciales.

La escala que aparece en el anterior mapa es 1:45.000.000, es decir, cada centrímetro en el mapa se corresponde con 45.000.000 centímetros, 450 kilometros, en la esfera terrestre. Aunque, como ya comentamos en la anterior entrada, no existen mapas correctos de la superficie terrestre, luego la escala de los mapas es mentira, solo es un valor aproximado.

Retrato 3: la proyección de Gall-Peters

El conocido como mapa de Peters es una de las historias de polémica y manipulación relacionadas con la cartografía.

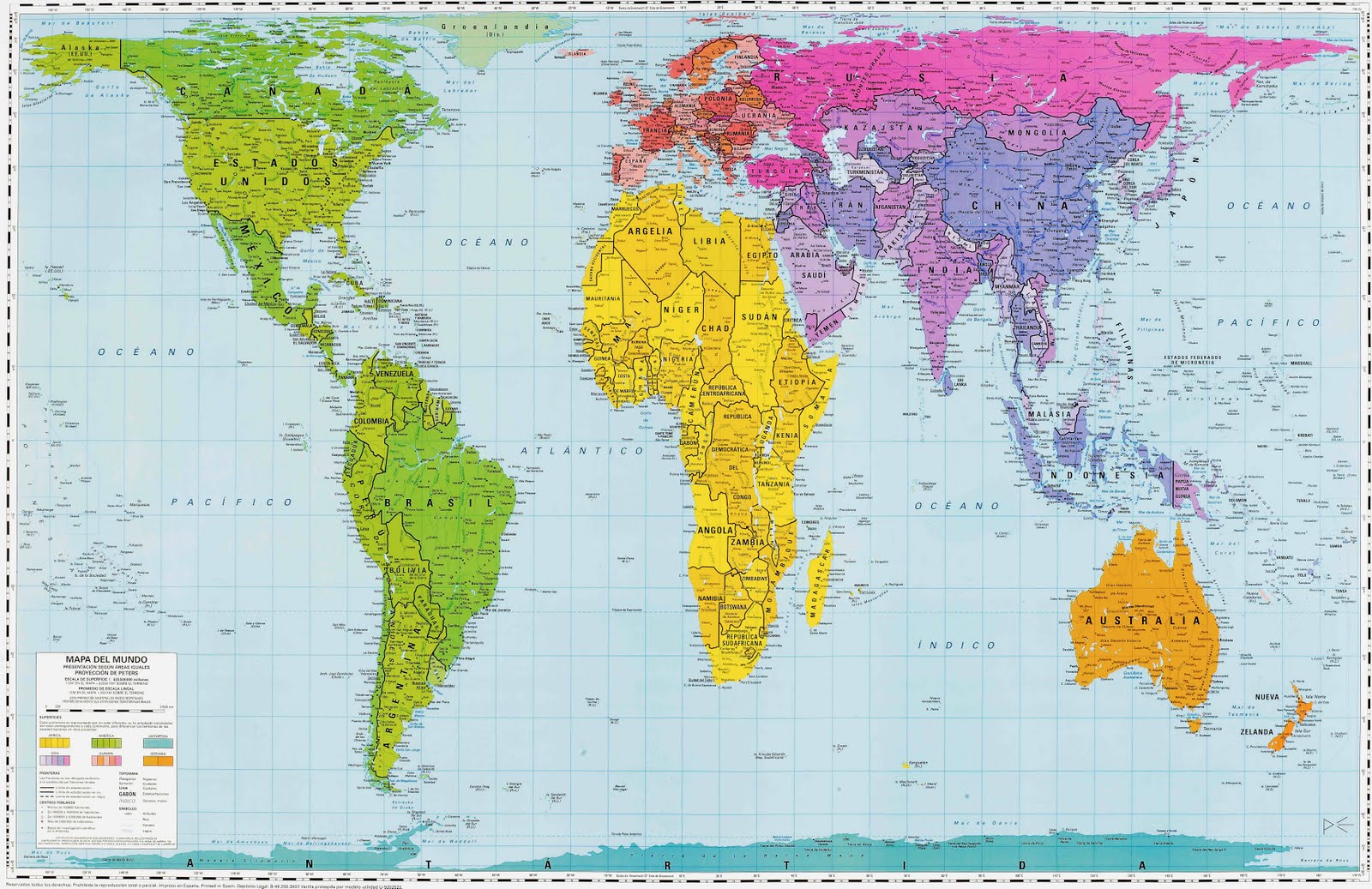
Pero primero expliquemos en qué consiste la proyección de Gall-Peters, para la mayoría conocida solo como la proyección de Peters, y la familia de proyecciones cilíndricas a la que pertenece.

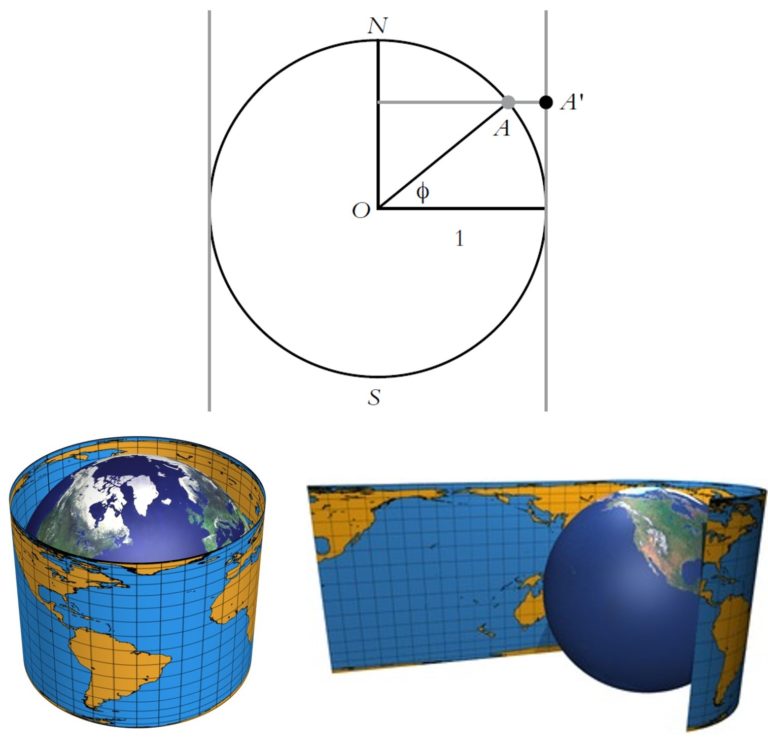
La familia de proyecciones cilíndricas (recordemos que eso significa que la esfera terrestre básica, es decir, el globo terrestre reducido primero a la escala que va a tener el mapa, se proyecta sobre un cilindro) isoareales (que preserva las áreas, salvo el factor de escala) a las que pertenece esta proyección tiene como punto de partida la proyección de Arquímedes o proyección cilíndrica isoareal de Lambert. Se proyecta la esfera terrestre básica, desde el eje de la misma, sobre el cilindro tagente a la esfera en el ecuador (como se muestra en la imagen), y después se despliega el cilindro, cortando por una de sus rectas generadoras, para obtener el mapa plano.

El mapa que se obtiene mediante dicha proyección es el mapa cilíndrico isoareal de Lambert, diseñado en 1772 por el matemático alemán Johann Heinrich Lambert (1728-1777), quien también demostró la irracionalidad del número π.

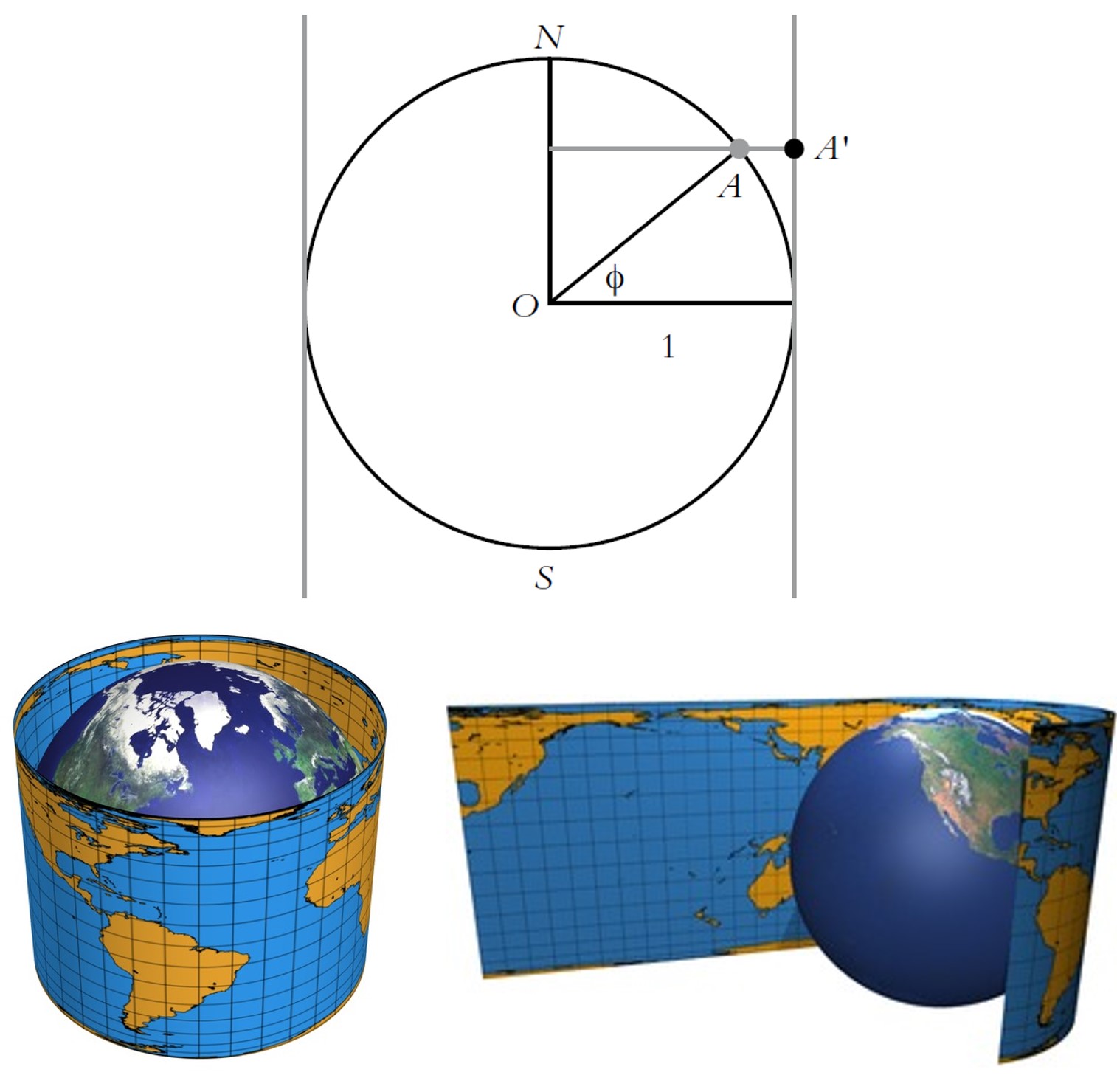
Se puede motificar esta proyección tomando, en lugar del cilindro tangente a la esfera terrestre básica, un cilindro secante a la misma (como en la imagen siguiente), es decir, que la interseca en un par de paralelos, equidistantes del ecuador.

Dependiendo de los paralelos en los que se intersecan la esfera terrestre básica y el cilindro se obtienen diferentes proyecciones cilíndricas isoareales. El clérigo escocés James Gall (1808-1895) diseñó, en 1855, el mapa para el paralelo de 45º, es decir, los paralelos 45º N y 45º S, aunque en 1967 la presentaría historiador alemán Arno Peters (1917-2002) como una proyección original suya. En 1910 el geógrafo alemán Walter Behrmann (1882-1955) diseñó el mapa para el paralelo de 30º, el arquitecto y cartógrafo aficionado Trystan Edwards (1884-1973) diseñó dos mapas para los paralelos 37,2º y 52º en 1953, o en el conocido mapa de Hobo-Dyer se utilizó, en 2002, el paralelo 37,3º para diseñar un mapa que se haría famoso por ser utilizado en un “mapa con el sur arriba”, y existen más.

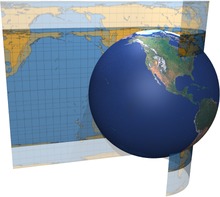
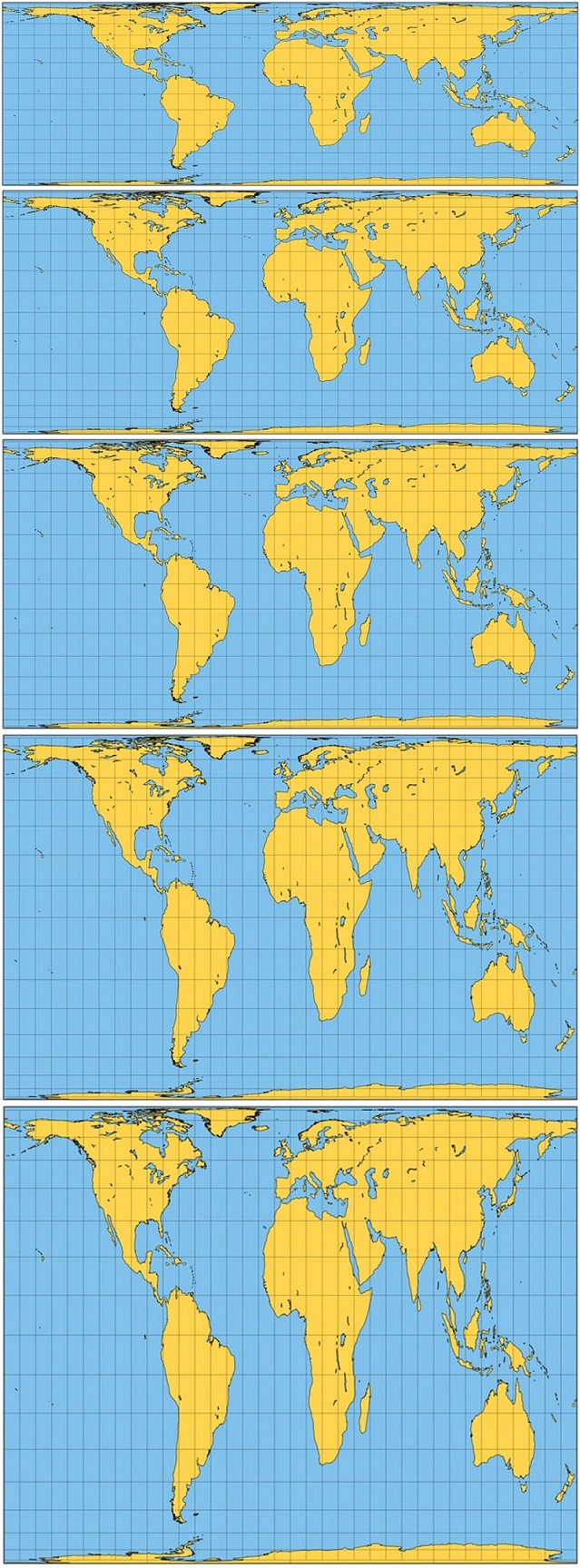
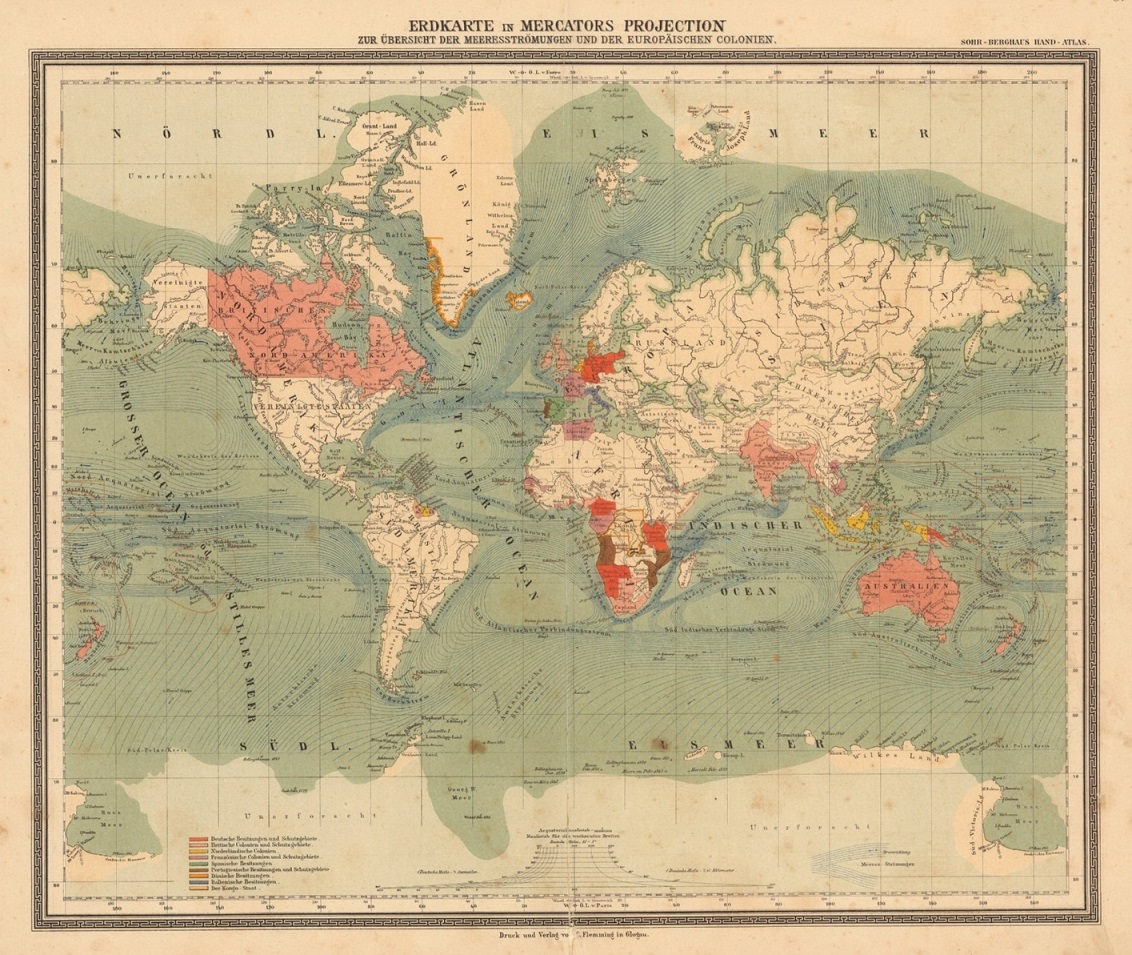
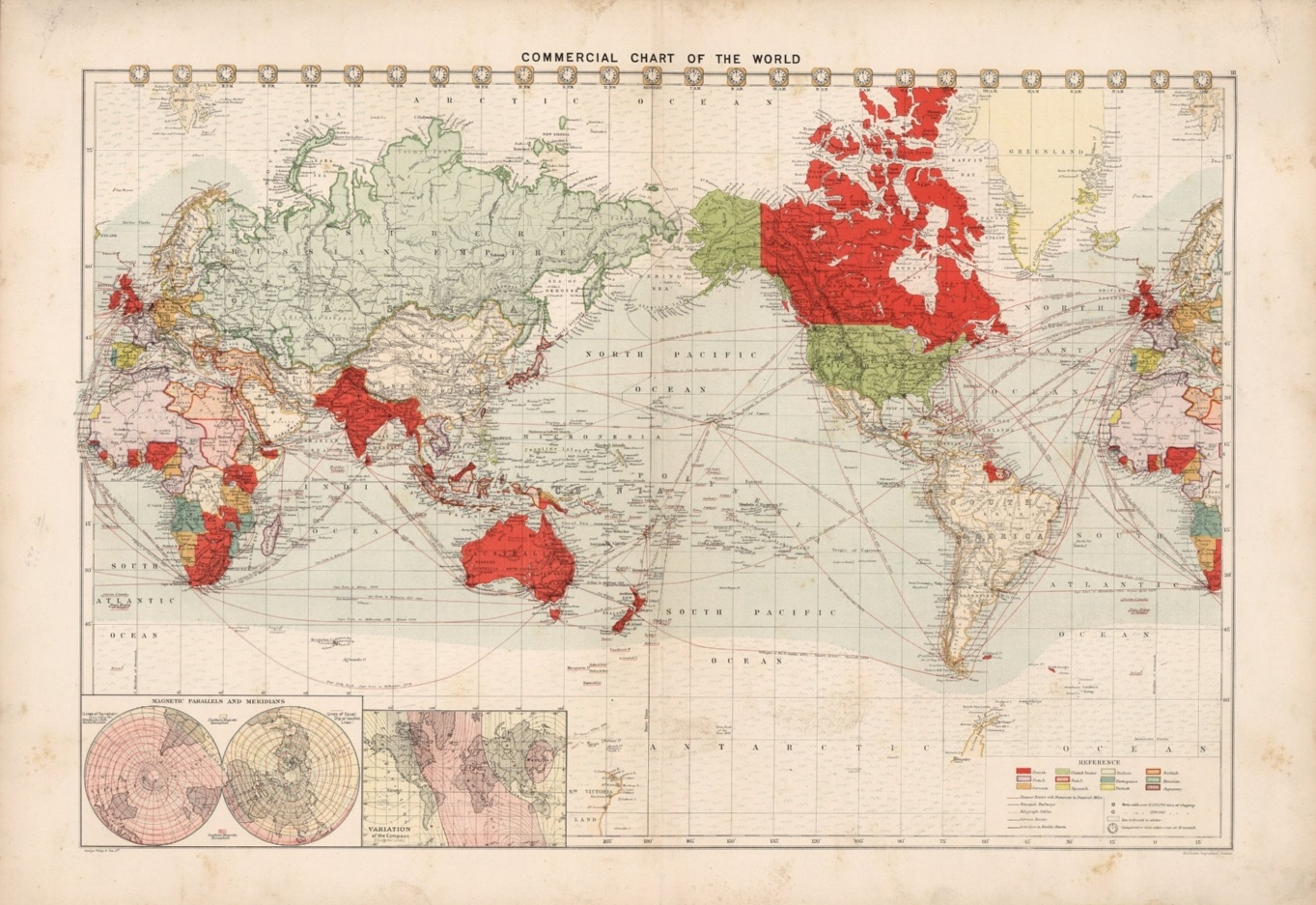
El historiador alemán Arno Peters presentó al mundo de la cartografía la proyección que lleva su nombre en 1967, en un congreso en la Academia de Ciencias de Hungría, pero el mundo científico no le hizo mucho caso, puesto que esa era una proyección ya conocida, había sido creada un siglo antes por el reverendo Gall. Sin embargo, en 1973 Arno Peters convocó a la prensa en Bonn y les presentó “su” mapamundi como la única alternativa posible, tanto desde el punto de vista de la justicia social como cartográfico, al mapa “racista” e inadecuado de Mercator. El argumento principal era que la proyección de Mercator distorsiona el área de las diferentes partes del mundo, mostrando las naciones del llamado “tercer mundo” (África, y centro y sur de América) pequeñas en comparación con las del llamado “primer mundo” (Norteamérica, Europa y Rusia). Tras su ataque al mapa de Mercator, mostró “su” mapamundi como la única alternativa posible.

Se originó un debate en el que, sin criterios científicos, los medios de comunicación y algunas organizaciones con preocupaciones humanitarias y religiosas defendieron y avalaron el mapa de Peters. Se pudieron escuchar expresiones como “la proyección de Mercator sobrevalora al hombre blanco y distorsiona la imagen del mundo para ventaja de los colonialistas” (Peters) o “el mapa de Peters corrige los errores del de Mercator […] es más riguroso desde el punto de vista científico”.

Arno Peters se aprovechó de la buena fe de las personas y de su solidaridad, así como de su desconocimiento de las mínimas nociones de la ciencia de la cartografía, para que reconocieran y apoyaran “su” mapa como el “único mapa solidario”, y lo que es peor, desde el punto de vista matemático y cartográfico, como “el único mapa correcto”.

Como sabemos, no existe ningún mapa correcto, ni el de Mercator, ni el de Peters, ni ningún otro. Cada proyección tiene sus propias propiedades positivas y negativas. La proyección de Mercator preserva los ángulos, los rumbos, y en su mapa las rectas representan los caminos de rumbo constante, tan útiles para la navegación (véase esta proyección en la entrada Imago mundi, 7 retratos del mundo), pero no preserva áreas, ni formas, ni caminos más cortos, y obviamente tampoco distancias. Por su parte, la proyección de Gall-Peters es efectivamente isoareal, preserva las áreas, pero no preserva ni ángulos, ni caminos más cortos, ni distancias y distorsiona bastante las formas (África y América del Sur están estiradas y Rusia, Canadá y Groenlandia comprimidas). Por otra parte, existen cientos de proyecciones, con los correspondientes mapas diseñados a partir de ellas, distintas, y muchas de ellas preservan las áreas, no solo la proyección de Gall-Peters, como toda la familia de proyecciones cilíndricas isoareales a la que pertenece o las proyecciones de Mollweide, Eckert IV o homolosena de Goode, que aparecen en la entrada Imago mundi, 7 retratos del mundo, y muchas más.

Retrato 4: la proyección de Robinson

Como ya comentamos en la entrada anterior de esta serie Imago mundi, el mapamundi de Mercator produce una fuerte distorsión cerca de los polos, en particular, en las áreas, lo que la hace inadecuada para mapas generales del mundo, mapas para la divulgación científica, la educación y los medios de comunicación. A pesar de ello, este mapamundi se sobre utilizó durante mucho tiempo. Sin embargo, a lo largo del siglo XX se fueron diseñando muchos mapas del mundo con otras proyecciones cartográficas más adecuadas e incluso se inventaban nuevas proyecciones con el objetivo de diseñar mapamundis generales más convenientes. En la entrada anterior mostramos algunos de esos ejemplos. Las siguientes proyecciones, de Robinson y de Winkel Tripel, son otros dos ejemplos.

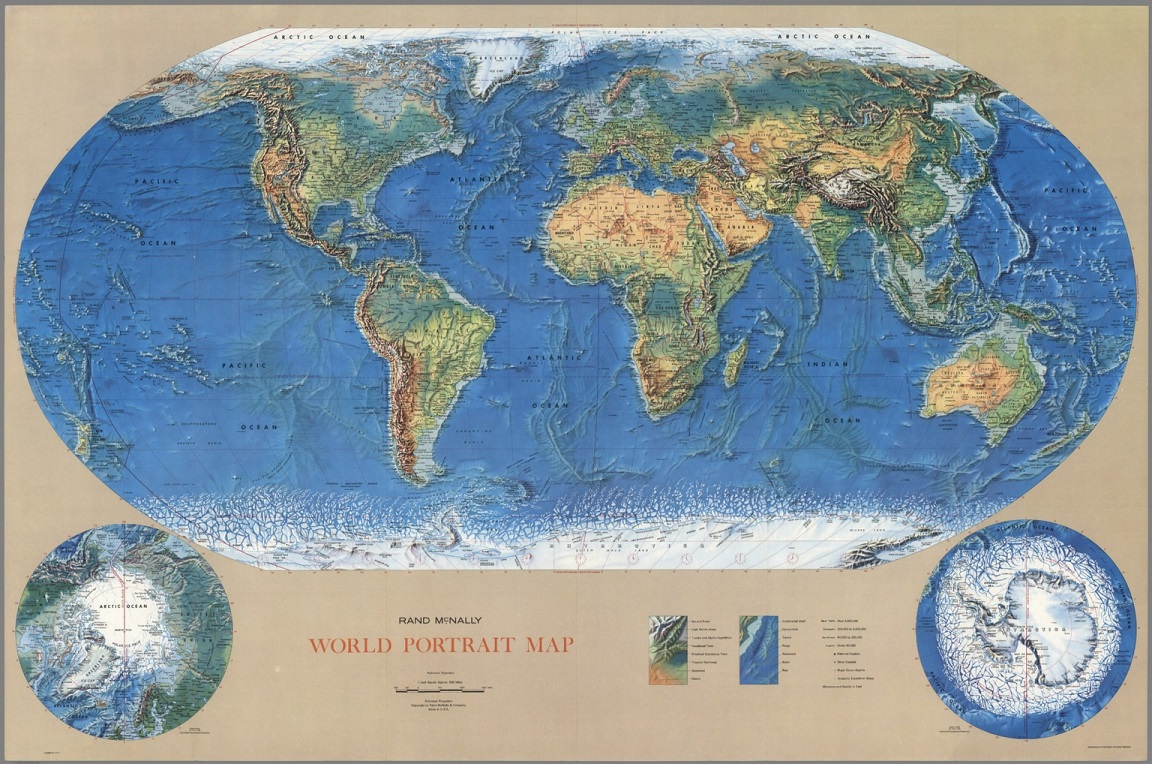
Rand McNally es una compañía norteamericana decicada a la tecnología y a la edición, famosa por sus publicaciones de atlas del mundo. La compañía estaba descontenta con las proyecciones cartográficas utilizadas para los mapas que representaban a todo el planeta, por lo que en 1961, solicitó al geógrafo y cartógrafo estadounidense Arthur H. Robinson (1915-2004), una proyección adecuada para el diseño del mapamundi, para lo que le pusieron una serie de condiciones, como que no fuera un mapa interrumpido, con la mínima deformación general posible, que no distorsionase mucho las áreas de los grandes continentes, con una red sencilla de meridianos y paralelos, y que fuese un mapa fácil de utilizar para cualquier edad. En 1974 el cartógrafo estadounidense publicó la nueva proyección psedo-cilíndrica que hoy se conoce como proyección de Robinson.

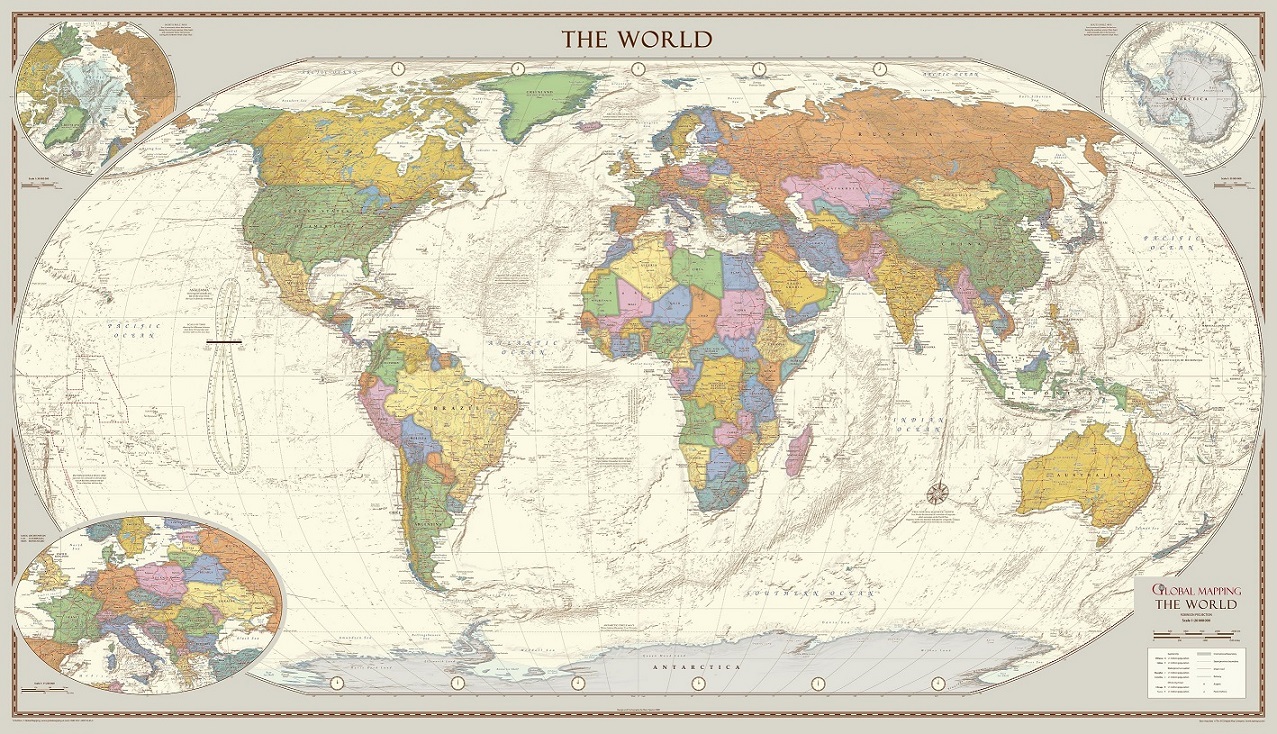
La National Geographic Society empezó a utilizar la proyección de Robinson para sus mapas del mundo entero en 1988, reeemplazando la proyección de Van der Gritten que había sido utilizada desde 1922, y fue reemplazada en 1998 por la proyección de Winkel tripel. Y fue utilizada también por muchas otras agencias.

Retrato 5: la proyección de Winkel tripel

Como acabamos de mencionar la National Geographic Society, que es un referente internacional, empezó a utilizar en 1998 la proyección de Winkel tripel para sus mapas generales del mundo.

Esta proyección es una de las tres creadas por el cartógrafo alemán Oswald Winkel (1874-1953) en 1921, como una media aritmética de otras dos proyecciones ya conocidas. En el caso de la proyección de Winkel tripel de la proyección rectangular (véase más arriba) y la proyeccion de Aitoff, una proyección creada a partir de la proyección azimutal equidistante (véase más abajo) propuesta por el cartógrafo y revolucionario ruso David A. Aitoff (1854-1933) en 1889.

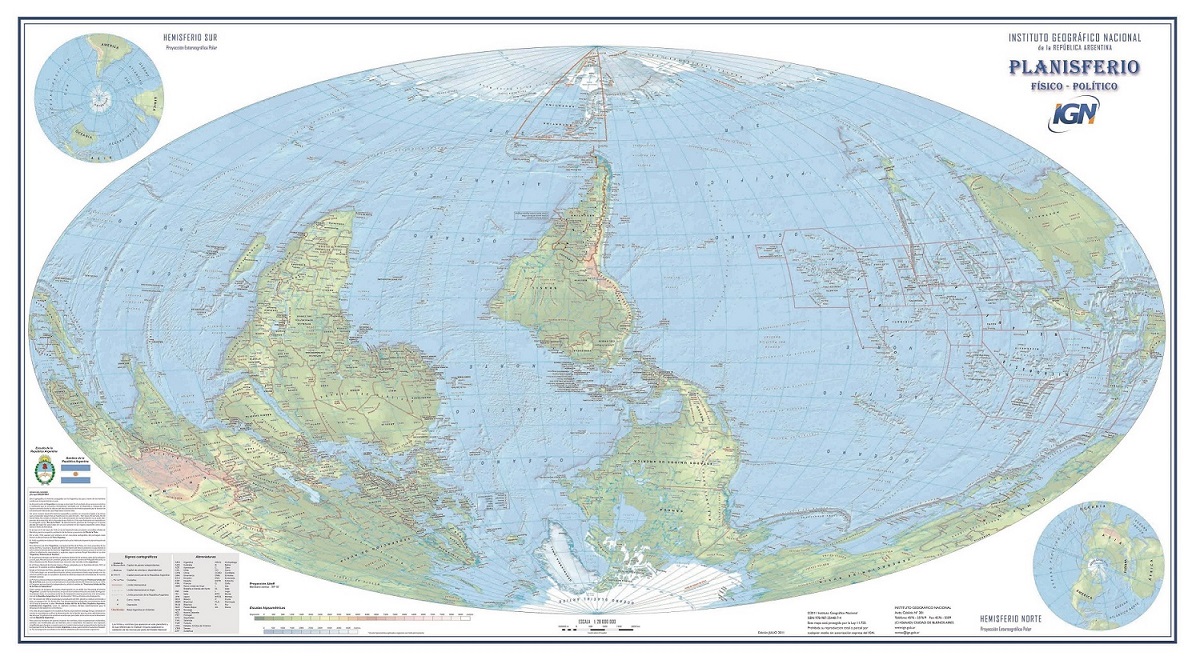
El nombre de “tripel” alude a la propiedad de la proyección de minimizar la distorsión de las tres propiedades métricas: área, ángulos y distancias.

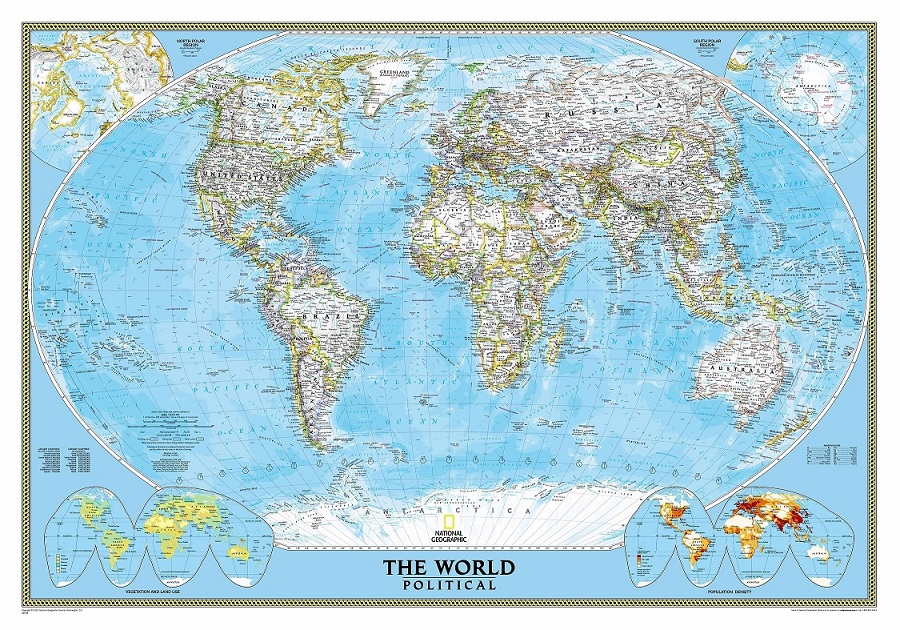
Después de que la National Geographic Society adoptase la proyección de Winkel tripel para sus mapas del mundo, muchas agencias, compañías y entidades educativas la utilizaron también para sus mapamundis. Aunque ya antes había sido utilizada también. Fue utilizada por primera vez para el Times Atlas of the World, editado por John Bartholomew & Sons, en 1955.

Retrato 6: la proyección acimutal equidistante

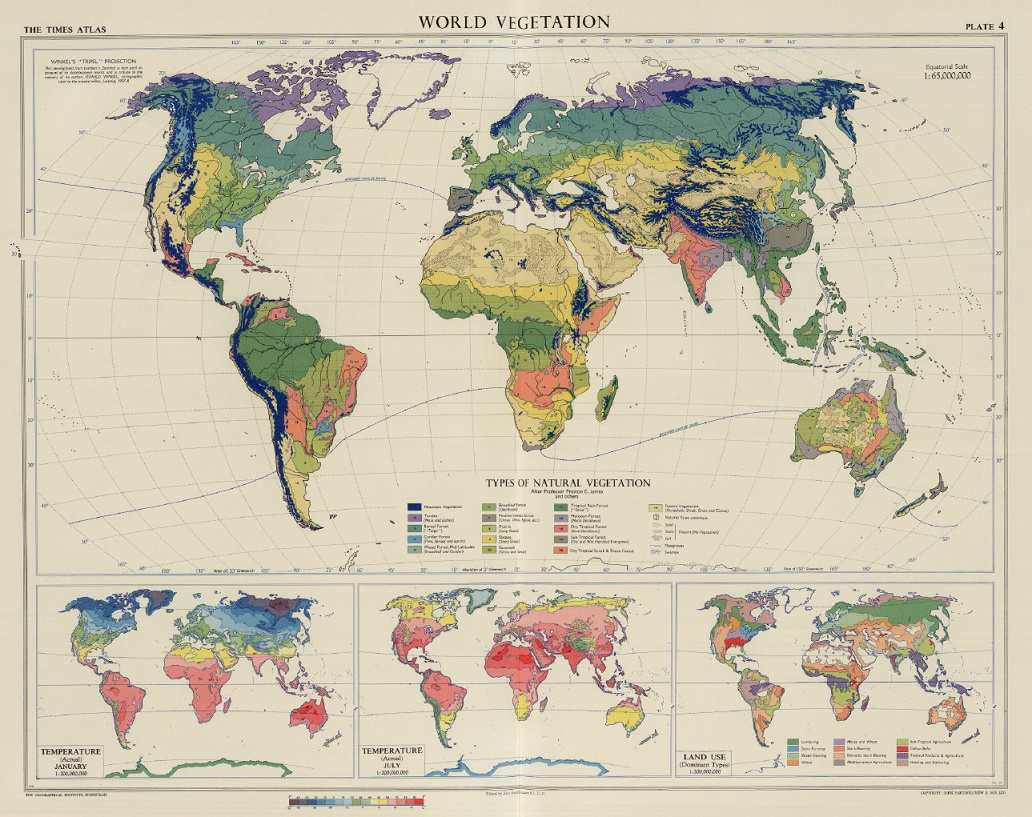
Al igual que las proyecciones gnomónica y estereográfica que presentamos en la anterior entrada, Imago mundi, 7 retratos del mundo, esta es una proyección acimutal, es decir, que se proyecta directamente sobre la esfera, sin pasar por una superficie auxiliar como el cilindro o el cono, aunque esta proyección, a diferencia de las otras, no es geométrica, no se deriva de una proyección a través de “rayos”. También es una proyección clásica, que ya debían utilizar los egipcios para los mapas celestes y que fue descrita por primera vez por el matemático iraní Al-Buruni (973-1050). La primera vez que se utilizó para elaborar mapas terrestres fue en el siglo XVI.

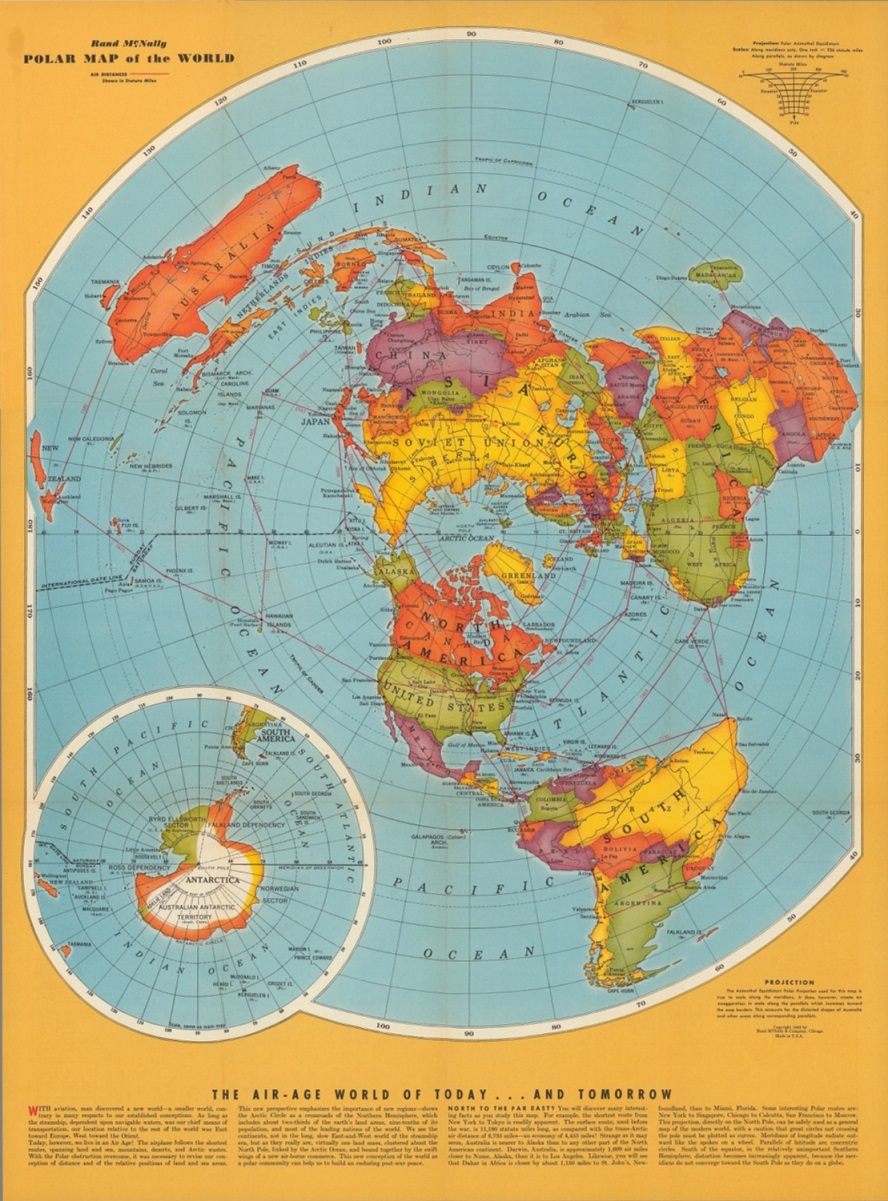
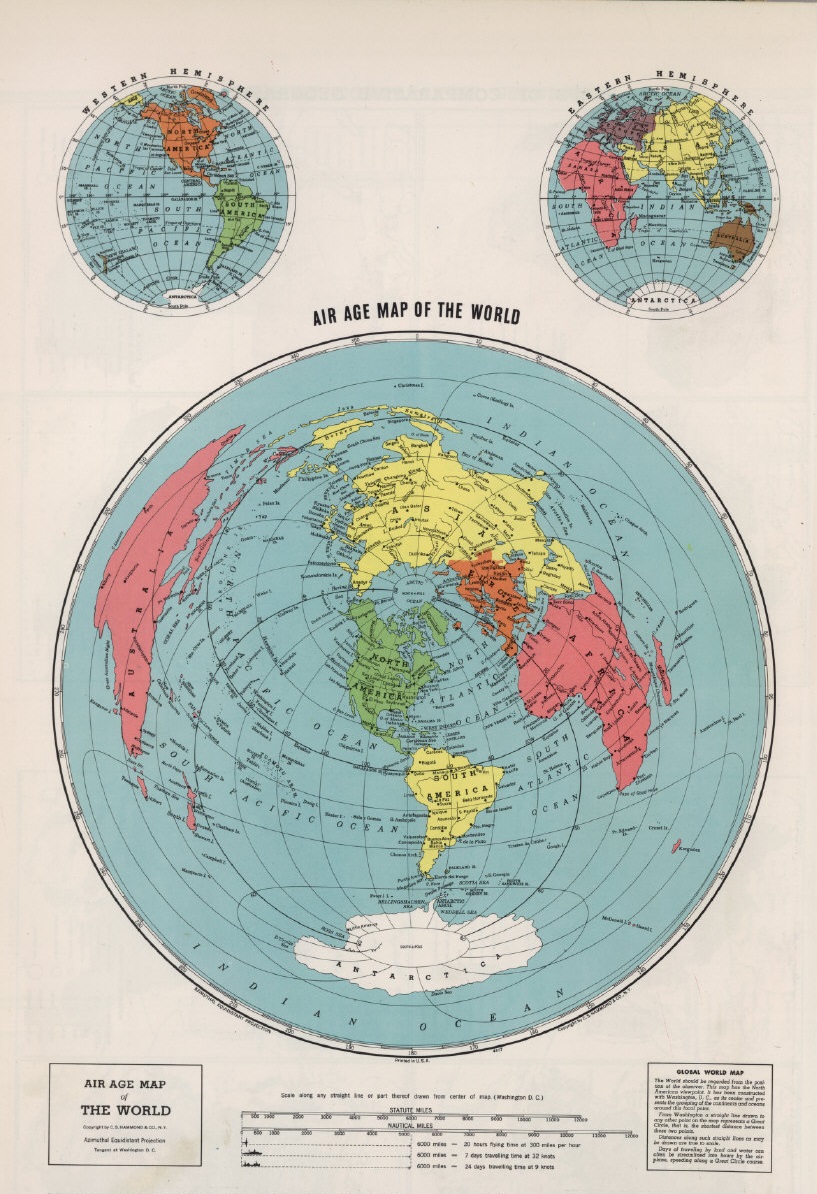
Al igual que otras proyecciones acimutales, satisface que las geodésicas, los círculos máximos de la esfera, que pasan por el punto central de referencia se transforman en rectas del plano que pasan por el centro del mapa. La propiedad particular de esta proyección es que la escala es constante a lo largo de dichas rectas, es decir, se preservan las distancias desde el centro del mapa.

Puede utilizarse para representar la totalidad de la superficie terrestre en un mapa plano, aunque la distorsión es muy fuerte al superar el semicírculo que está a la mitad de la distancia del centro. En la versión polar del mapa, que es la que aparece en la imagen anterior o en el mapa de la Organización de Naciones Unidas, los meridianos son las rectas radiales que emanan del centro, el polo, y los paralelos son circunferencias concéntricas igualmente espaciadas.

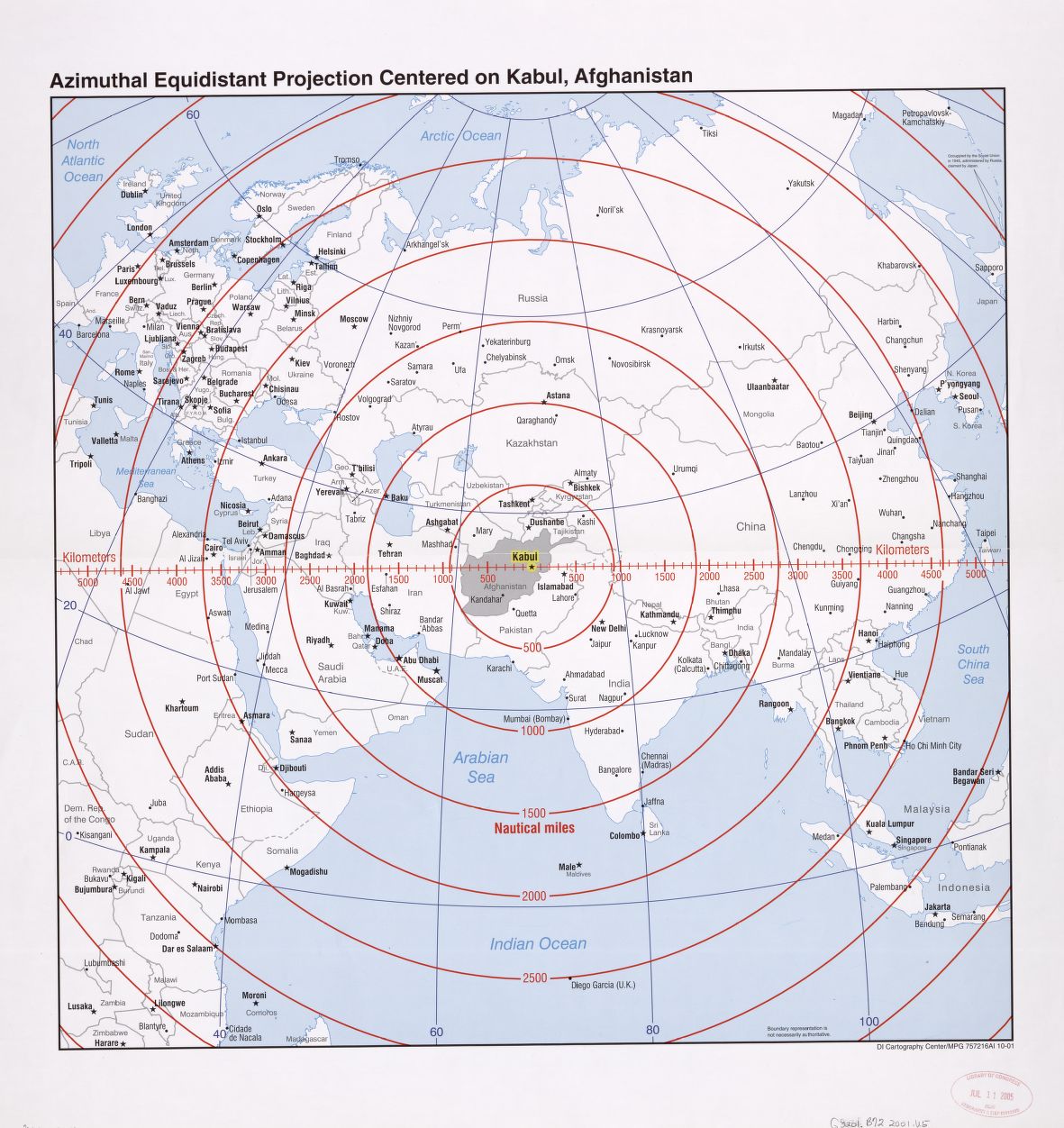
Es una proyección ampliamente utilizada, en muchas ocasiones para representar las zonas polares como acompañante de los mapamundis diseñados con otras proyecciones, pero también para mapas de un solo hemisferio. Se suele llamar también “mapa egocéntrico” ya que posee un punto central, que se convierte en el mapa del mundo, y desde el que se preservan las distancias.

Aunque estamos hablando en estas entradas de mapas del mundo, las proyecciones se utilizan para mapas de regiones más pequeñas, así esta proyección se utiliza para mapas centrados en un lugar concreto desde donde se quiere conocer los puntos que están a unas ciertas distancias, que como esta proyección preserva las distancias desde el centro se representan como circunferencias.

No hemos tenido tiempo de hablar de algunas proyecciones cónicas, de las proyecciones acimutales ortográfica y de perspectiva, de la proyección de armadillo, o de algunas proyecciones singulares, a las cuales dedicaremos la tercera y última entrega de esta serie del Cuaderno de Cultura Científica, Imago Mundi.

Para terminar, la instalación World Map (2013) del artista sudafricano, aunque afincado en Londres, Clinton de Menezes, que desgraciadamente fue asesinado en la nochevieja de 2013 en su país natal.

Bibliografía

1.- Raúl Ibáñez, El sueño del mapa perfecto; cartografía y matemáticas, RBA, 2010.

2.- Raúl Ibáñez, Muerte de un cartógrafo, Un paseo por la Geometría, UPV/EHU, 2002. Versión online en la sección textos-on-line de divulgamat

3.- Timothy G. Feeman, Portraits of the Earth; A Mathematician looks at Maps, AMS, 2002.

4.- David Rumsey Map Collection

5.- J. P. Snyder, Flattening the Earth, Two Thousand Years of Map Projections, The University of Chicago Press, 1993.

6.- Carlos Furuti, Map projections

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica