Muchas de las perturbaciones que hemos considerado hasta ahora han sido repentinas y de corta duración, creadas por un breve movimiento como un latigazo en el extremo de una cuerda o un desplazamiento repentino en el extremo de un tren. En cada caso, vemos una onda que corre a lo largo del medio con una cierta velocidad. Ya hemos mencionado que este tipo de onda se llama pulso.

Consideremos ahora ondas periódicas, esto es, perturbaciones rítmicas regulares y continuas en un medio que resultan de la vibración periódica de una fuente. Un buen ejemplo de un objeto en vibración periódica es un péndulo oscilante. Dejando de lado los efectos de la resistencia del aire, cada oscilación es virtualmente idéntica a cualquier otra oscilación, y esta oscilación se repite una y otra vez en el tiempo.

Otro ejemplo es el movimiento hacia arriba y hacia abajo de un peso en el extremo de un muelle. En cada caso, el desplazamiento máximo desde la posición de equilibrio se llama amplitud, A, como se muestra en la imagen más abajo para el caso del muelle. El tiempo empleado en completar una vibración se denomina período, T, expresado habitualmente en segundos. El número de vibraciones por segundo se llama frecuencia, f. A la vista de estas definiciones debería ser evidente que T y f son recíprocos, es decir, T = 1 / f.

¿Qué sucede cuando se aplica una vibración periódica al extremo de una cuerda? Supongamos que el extremo izquierdo de una cuerda tensa se sujeta al peso oscilante (vibrante) que está en el extremo de un muelle vertical. A medida que el peso vibra hacia arriba y hacia abajo observamos una onda que se propaga a lo largo de la cuerda, como vemos en la siguiente imagen.

La onda toma la forma de una serie de crestas y valles a lo largo de la cuerda. La fuente ejecuta un movimiento armónico simple hacia arriba y hacia abajo. Idealmente, cada punto a lo largo de la cuerda ejecuta también un movimiento armónico simple. La onda viaja hacia la derecha a medida que crestas y valles se suceden. Cada punto o segmento pequeño a lo largo de la cuerda simplemente oscila hacia arriba y hacia abajo a la misma frecuencia que la fuente. La amplitud de la onda está representada por A. La distancia entre dos crestas consecutivas o dos depresiones consecutivas es la misma en toda la longitud de la cuerda. Esta distancia, llamada longitud de onda de la onda periódica, se representa convencionalmente por la letra griega λ (lambda).

La velocidad de una onda periódica se puede encontrar indirectamente si se puede medir su frecuencia y su longitud de onda. Para ilustrarlo usaremos el ejemplo de la onda en la cuerda. Sabemos que a medida que la onda avanza cada punto del medio oscila con la frecuencia y el período de la fuente. La imagen siguiente ilustra una onda periódica que se mueve hacia la derecha, representada por instantáneas tomadas cada cuarto de período, T.

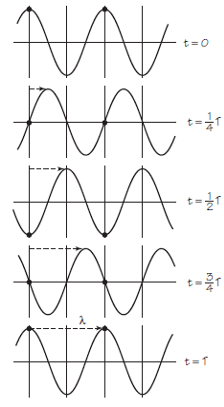
Sigamos el progreso de la cresta que comenzó desde el extremo izquierdo en el tiempo t = 0. El tiempo que tarda esta cresta en moverse una distancia de una longitud de onda es igual al tiempo requerido para una oscilación completa de la fuente, o de cualquier punto en la cuerda; es decir, la cresta mueve una longitud de onda durante un período de oscilación T. La velocidad v de la cresta, por lo tanto, viene dada por la ecuación v = distancia recorrida / tiempo empleado = λ / T.

Todas las partes de la forma de la onda se propagan con la misma velocidad a lo largo de la cuerda. Por lo tanto, la velocidad de cualquier cresta es la misma que la velocidad de la onda en su conjunto. Por lo tanto, la velocidad v de la onda también está dada por v = longitud de onda / periodo = λ / T.

Pero, hemos visto antes que T = 1 / f , lo que es equivalente a f = 1 / T, por tanto también podemos decir que la velocidad de una onda es v = λ· f. De aquí se sigue queλ = v / f y que f = v / λ. Estas expresiones muestran que, para ondas de la misma velocidad, la frecuencia y la longitud de onda son inversamente proporcionales; es decir, una onda con una frecuencia doble que otra que se desplaza a la misma velocidad tendría solo la mitad de la longitud de onda, y así sucesivamente. Esta relación inversa de frecuencia y longitud de onda es algo que es necesario tener siempre en mente cuando hablemos de ondas.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance