El concepto de fase no es en sí mismo complicado. La palabra fase suele emplearse habitualmente para indicar cada uno de los distintos estados sucesivos de un fenómeno natural (o histórico). Decimos habitualmente, pero hemos de ser conscientes de que no siempre para evitar errores. Así, por ejemplo, también se llama fase a una parte homogénea con límites bien definidos de un sistema heterogéneo, un concepto que, si bien tiene su origen en el uso habitual (el agua solida al calentarse pasa sucesivamente a una fase líquida y después a una fase vapor, por ejemplo), es un concepto actualmente independiente de la idea de estado sucesivo.

El concepto de fase es fundamental para entender el funcionamiento de una onda periódica. El siguiente diagrama representa una onda periódica que pasa a través de un medio. En él aparecen marcados conjuntos de puntos que se mueven «a la vez y de la misma forma» a medida que pasa la onda periódica. Los puntos cresta C y C’ han alcanzado posiciones máximas hacia arriba. Los puntos valle D y D’ han alcanzado posiciones máximas hacia abajo. Los puntos C y C’ tienen desplazamientos y velocidades idénticos en cualquier instante de tiempo. Sus vibraciones son idénticas y van al unísono. Lo mismo ocurre con los puntos D y D’. De hecho hay infinitos pares de puntos a lo largo del medio que vibran de manera idéntica cuando pasa esta onda. Démonos cuenta de que C y C’ están separados una distancia igual a una longitud de onda, λ, al igual que D y D’.

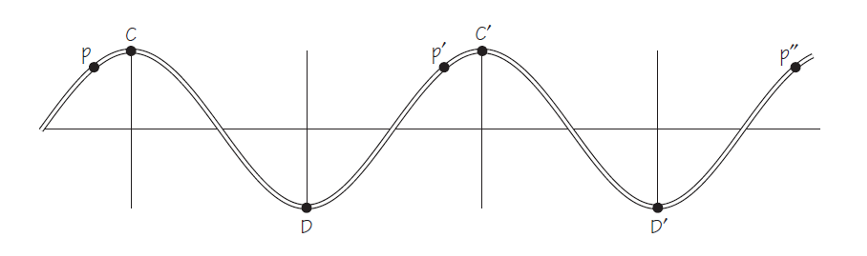
Los puntos que se mueven al unísono, como C y C’, se dice que están en fase entre sí. Los puntos D y D’ también se mueven en fase. De hecho, los puntos separados entre sí por distancias de λ, 2λ, 3λ,. . . o, en general, nλ (siendo n cualquier número entero) están todos en fase entre sí. Estos puntos pueden estar en cualquier lugar (fase) a lo largo de la longitud de la onda. No necesitan corresponderse solo con los puntos más altos o más bajos. Así, puntos como P, P’, P», están todos en fase entre sí. Cada uno de estos puntos está separado por una distancia λ del siguiente que está en fase con él.

Por otro lado, también podemos ver que algunos pares de puntos están fuera de sincronía. Por ejemplo, el punto C alcanza su máximo desplazamiento hacia arriba al mismo tiempo que D alcanza su máximo desplazamiento hacia abajo. En el instante en que C comienza a bajar, D comienza a subir (y viceversa). Puntos como estos están medio período fuera de fase entre sí. C y D’ también están medio período fuera de fase. Cualquiera dos puntos separados entre sí por distancias de 1⁄2λ , 3/2λ , 5⁄2 λ, etc., están medio período fuera de fase.

En esta serie hacemos hincapié en las ideas, pero entendemos que las matemáticas son la mejor forma de expresarlas de forma eficaz y eficiente, auqnue no nos metamos a fondo con ellas. Si pretendemos representar una onda periódica y sus características en un plano XY, entonces la posición (x,y) de un punto cualquiera en función del tiempo, t, viene dada por la siguiente ecuación de onda:

y(x, t) = A sen (ωt + kx + δ),

donde A es la amplitud, ω es la velocidad angular dada por ω = 2π/T (donde T es el periodo), k es el número de onda dado por k = 2π/λ y δ el desfase. La fórmula parece que es ciencia infusa, pero con los conceptos que hemos visto y este fantástico vídeo de José Luis Crespo, la entenderás perfectamente (incluso sin tener ni idea de trigonometría):

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance