Con los conceptos que hemos visto ya estamos en disposición de explorar un territorio fascinante. Hasta ahora hemos considerado ondas individuales. ¿Qué ocurre cuando se encuentran dos ondas en el mismo medio? Supongamos que dos ondas se aproximan la una a la otra en una cuerda, una se desplaza hacia la derecha y la otra hacia la izquierda. La serie de imágenes de la Figura 1 muestra lo que sucedería si hiciéramos este experimento. Las ondas se atraviesan la una a la otra sin sufrir modificación alguna. ¿Te sorprende? No debería.

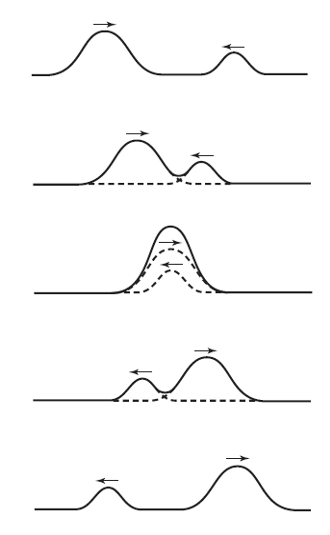
Después del encuentro, cada onda tiene el mismo aspecto que antes del mismo y sigue avanzando como antes. (¡Algo completamente diferente al encuentro de dos partículas!). Este fenómeno de ondas que se atraviesan sin ser alteradas se puede observar con todos los tipos de ondas. Se puede ver experimentalmente muy fácilmente en las ondulaciones superficiales en el agua. También ocurre con las ondas de sonido, la prueba la tenemos en que alrededor de una mesa pueden mantenerse varias conversaciones al mismo tiempo sin que se distorsionen entre sí, no digamos ya en una discoteca.

¿Qué sucede durante el tiempo en que en el que las dos ondas estás superpuestas? Los desplazamientos que provocan se suman en cada punto del medio. Dicho de otra manera, el desplazamiento de cualquier punto en la región de superposición es solo la suma de los desplazamientos que serían causados en ese momento por cada una de las dos ondas por separado, como se muestra en la Figura 1. En esta figura vemos dos ondas que se desplazan en sentidos opuestos en una cuerda. Una tiene un desplazamiento máximo de 0,4 cm hacia arriba y la otra un desplazamiento máximo de 0,8 cm hacia arriba. El desplazamiento total máximo hacia arriba de la cuerda en un punto en el que estas dos ondas se cruzan será de 1,2 cm.

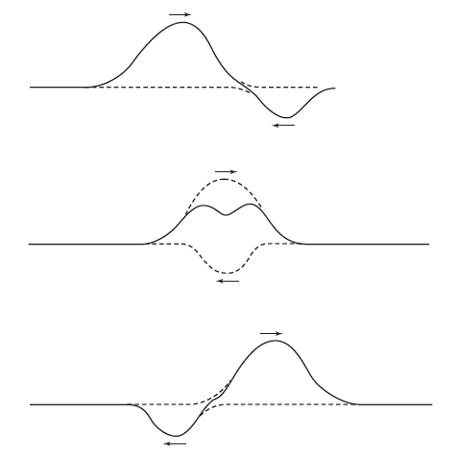
Este comportamiento de las ondas es muy simple y facilita mucho las cosas. Veámoslo. Cada onda avanza a lo largo de la cuerda haciendo su propia contribución al desplazamiento de la cuerda sin importar lo que haga cualquier otra onda. Esta propiedad de las ondas se llama superposición. Usándolo podemos determinar fácilmente de antemano qué aspecto tendrá la cuerda en cualquier momento dado. Todo lo que hay que hacer es sumar los desplazamientos que causará cada onda en cada punto a lo largo de la cuerda en ese instante. La figura 2 muestra una superposición de ondas más general, en la que una de ellas provoca desplazamientos negativos; los desplazamientos se siguen sumando, cada uno con su signo. Esto significa que si los desplazamientos son en sentidos opuestos tienden a cancelarse entre sí.

El principio de superposición se aplica sin importar cuántas ondas o perturbaciones individuales estén presentes en el medio. En los ejemplos que acabamos de ver solo había dos ondas. Pero, experimentalmente se comprueba (en la discoteca mismo) que el principio de superposición funciona igual de bien para tres, diez o cualquier cantidad de ondas. Cada una hace su propia contribución, y el resultado neto es simplemente la suma de todas las contribuciones individuales (Figura 3).

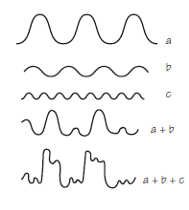
Si las ondas se agregan como acabamos de describir, de ahí se sigue que podemos considerar cualquier onda compleja como la suma de un conjunto de ondas (sinusoidales) simples. En 1807, el matemático francés Augustin Jean Fourier presentó un teorema muy útil. Fourier afirmó que cualquier oscilación periódica continua, por compleja que sea, puede analizarse como la suma de movimientos de onda más simples.

Esto también se demuestra experimentalmente. Los sonidos de los instrumentos musicales también se pueden analizar de esta manera y este análisis de Fourier (o análisis armónico) permite «imitar» los instrumentos electrónicamente combinando y emitiendo las proporciones correctas de vibraciones simples, que corresponden a tonos puros.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance