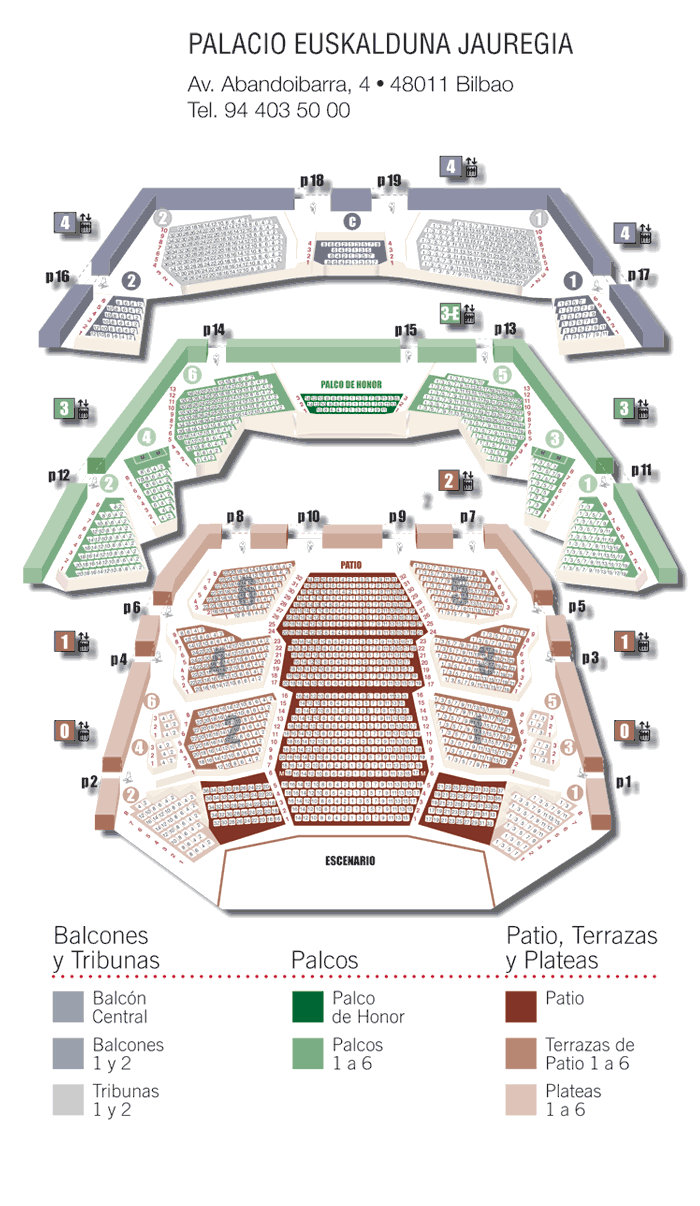
Ya hemos visto el patrón de interferencia en pulsos de ondas. Vamos ahora a dar el siguiente paso considerando ondas periódicas.

Cuando se emiten dos ondas periódicas de igual amplitud en lugar de pulsos individuales, se produce una superposición en toda la superficie, como también se muestra en la Figura 1. A lo largo de la línea de puntos central de la figura, hay una amplitud de la perturbación doble. A lo largo de las líneas etiquetadas con N, la altura del agua permanece inalterada. Dependiendo de la longitud de onda y la distancia entre las fuentes, puede haber muchas líneas de interferencia constructiva y destructiva.

Ahora podemos interpretar el patrón de interferencia de la Figura 2 (que ya apareció al hablar de pulsos de ondas). Las bandas grises son áreas donde las ondas se cancelan entre sí en todo momento; se las llama líneas nodales. Estas bandas corresponden a las líneas etiquetadas como N en la Figura 1. Entre estas bandas hay otras bandas donde la cresta y el valle se suceden, donde las ondas se refuerzan. Estas se llaman líneas antinodales.

Este patrón de interferencia se establece mediante la superposición de ondas de dos fuentes. Para las ondas en el agua, el patrón de interferencia se puede ver directamente. Pero ya sean visibles o no, todas las ondas, incluidas las ondas de de los terremotos, las ondas del sonido o los rayos X, pueden establecer patrones de interferencia. Por ejemplo, supongamos que dos altavoces alimentados por el mismo reproductor funcionan a la misma frecuencia. Al cambiar nuestra posición frente a los altavoces podemos encontrar las regiones nodales donde las interferencias destructivas hacen que solo se escuche un sonido débil. También podemos encontrar las regiones antinodales en las que se recibe una señal fuerte. Por ello el precio de las butacas en los auditorios de música varía más por el patrón de difracción (muy complejo en este caso) del sonido y no tanto por la visibilidad de la orquesta.

La hermosa simetría de estos patrones de interferencia no es accidental. Más bien, todo el patrón está determinado por la longitud de onda λ y la separación de las fuentes d. A partir de estos datos se pueden calcular los ángulos en los que las líneas nodal y antinodal se extienden a ambos lados de A₀.

Pero de aquí se sigue algo mucho más interesante. A la inversa, es posible que conozcamos d, y podemos encontrar los ángulos estudiando el patrón de interferencia. En este caso podemos calcular la longitud de onda incluso si no podemos ver las crestas y valles de las ondas directamente. Esto es muy útil porque la mayoría de las ondas en la naturaleza no se pueden ver directamente. Para averiguar su longitud de onda se debe estudiar el patrón de interferencia, buscar las líneas nodales y antinodales y calcular λ a partir de la geometría.

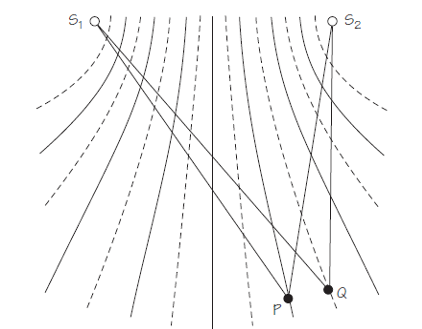
La Figura 3 muestra parte del patrón de la Figura 1. En cualquier punto P de una línea antinodal las ondas de las dos fuentes llegan en fase. Esto puede ocurrir solo si P está igual de lejos de S₁ y que de S₂, o si P está un número entero de longitudes de onda más lejos de una fuente que de la otra. En otras palabras, la diferencia en distancias (S₁P – S₂P) debe ser igual a nλ, siendo λ la longitud de onda y n cero o cualquier número entero. En cualquier punto Q de una línea nodal las ondas de las dos fuentes llegan exactamente fuera de fase. Esto ocurre porque Q está un número impar de medias longitudes de onda (1⁄2λ, 3⁄2λ, 5⁄2λ, etc.) más lejos de una fuente que de la otra. Esta condición se puede escribir S₁Q – S₂Q = (n + 1⁄2)λ.

La distancia desde las fuentes hasta un punto de detección puede ser mucho mayor que la separación de las fuentes d. En ese caso, existe una relación simple entre la posición del nodo, la longitud de onda λ y la separación d. La longitud de onda se puede calcular a partir de las mediciones de las posiciones de las líneas nodales.

Este tipo de análisis permite calcular a partir de mediciones simples realizadas en un patrón de interferencia la longitud de onda de cualquier onda. Esto se aplica rutinariamente a las ondulaciones en el agua, al sonido a todas las escalas o a la luz en todas sus manifestaciones. Este concepto tan simple tiene unos usos impresionantes: desde el estudio del núcleo de la Tierra estudiando las ondas de los terremotos, a las colisiones de agujeros negros que provocan ondas gravitacionales, pasando por el diseño y tarificación de salas de concierto.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance