La razón física de la aparición de notas armoniosas y la relación entre ellas no eran cosas conocidas por los griegos. Pero utilizando el principio de superposición podemos comprender y definir las relaciones armónicas de manera mucho más precisa.

Primero, debemos enfatizar un hecho importante sobre los patrones de onda estacionarios producidos al reflejarse las ondas en los límites de un medio. Podemos imaginar una variedad ilimitada de ondas viajando de un lado a otro. Pero, de hecho, solo ciertas longitudes de onda (o frecuencias) pueden producir ondas estacionarias en un medio dado. En el ejemplo de un instrumento de cuerda, los dos extremos de cada cuerda están fijos (por los enganches de cada cuerda, en el caso de un arpa, o por el enganche y la presión de un dedo en el caso de una guitarra) y, por lo tanto, deben ser puntos nodales.

Este hecho pone un límite superior a la longitud de las ondas estacionarias posibles en una cuerda fijada en ambos extremos de longitud l. Dada la condición de que los extremos son puntos nodales, es evidente que dicho límite se corresponde con aquella onda para la que la mitad de su longitud de onda coincide con la de la cuerda o, expresado matemáticamente, l = λ/2 (Figura 1, arriba-izquierda).

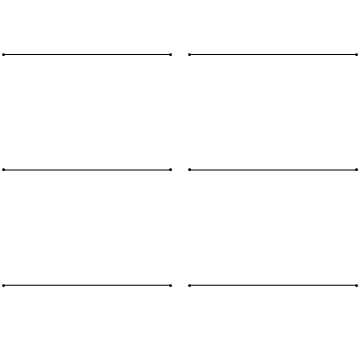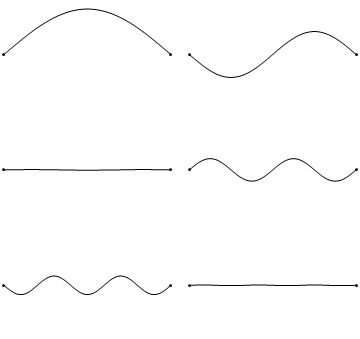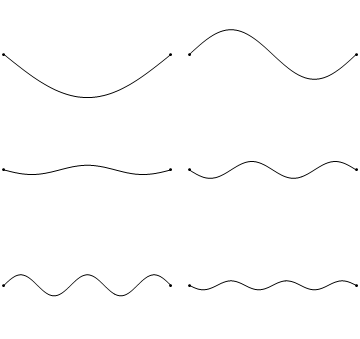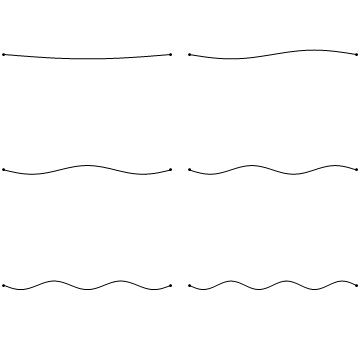
Ondas más cortas también pueden producir patrones estacionarios pero, eso sí, teniendo más nodos. En cualquier caso debe cumplirse siempre que algún número entero n de medias longitudes de onda media coincide con la longitud de la cuerda, de modo que l = nλ/2 .

Visto de otro modo, la imagen arriba-izquierda de la Figura 1 podemos decir que representa una onda de λ = 2l (fíjate que es idéntico a lo que hemos dicho arriba, pero dado la vuelta). La de arriba-derecha una de λ = 1/2 (2l); la de centro-izquierda λ = 1/3(2l); y así sucesivamente.

La relación matemática general que da la expresión para todas las longitudes de onda posibles de las ondas estacionarias en una cuerda fija es, por tanto, λ_n = 2l /n, donde n es un número entero. También podemos decir, simplemente que la longitud de onda es inversamente proporcional a n, es decir, λ ∝ 1/n.

Es decir, si λ₁ es la longitud de onda más larga posible, las otras longitudes de onda posibles serán 1/2 λ₁, 1/3 λ₁, …, (1/n) λ₁. Las longitudes de onda más cortas corresponden a frecuencias más altas. Por lo tanto, en cualquier medio acotado solo se pueden establecer ciertas frecuencias concretas de ondas estacionarias. Dado que la frecuencia f es inversamente proporcional a longitud de onda, f ∝ 1 / λ, podemos reescribir la expresión para todas las posibles ondas estacionarias en una cuerda pulsada como f_n ∝ n.

En otras circunstancias, f_n puede depender de n de alguna otra manera. La frecuencia más baja posible de una onda estacionaria es generalmente la que está más presente cuando la cuerda vibra después de ser pulsada o arqueada. Si f₁ representa la frecuencia más baja posible, entonces las otras ondas estacionarias posibles tendrían las frecuencias 2f₁ , 3f₁ ,. . . , nf₁ . Estas frecuencias más altas se denominan «sobretonos» de la frecuencia «fundamental» f₁. En una cuerda «ideal», hay en principio un número ilimitado de estas frecuencias, pero cada una de ellas es un múltiplo simple de la frecuencia más baja.

En los medios reales existen límites superiores prácticos para las posibles frecuencias. Además, los sobretonos no son exactamente múltiplos simples de la frecuencia fundamental; es decir, los sobretonos no son estrictamente «armónicos». Este efecto es aún mayor en los sistemas más complejos que las cuerdas tensas. En una flauta, saxofón u otro instrumento de viento, se crea una onda estacionaria en una columna de aire. Dependiendo de la forma del instrumento, los sobretonos producidos pueden no ser ni siquiera aproximadamente armónicos.

Como podemos intuir a partir del principio de superposición, las ondas estacionarias de diferentes frecuencias pueden existir en el mismo medio al mismo tiempo. Una cuerda de guitarra fuertemente pulsada, por ejemplo, oscila en un patrón que es la superposición de las ondas estacionarias de muchos sobretonos. Las energías de oscilación relativas de los diferentes instrumentos determinan la «calidad» del sonido que producen. Cada tipo de instrumento tiene su propio equilibrio de sobretonos. Es por eso que un violín suena diferente a una trompeta, y ambos suenan diferente a una voz de soprano, incluso si todos suenan a la misma frecuencia fundamental.

Como ilustración sonora, Xaver Varnus juega con columnas de aire de distinta longitud en las que se provocan ondas estacionarias de distintas longitudes de onda y, por tanto, frecuencias fundamentales, con los sobretonos particulares del órgano de la catedral de Berlín, interpretando a Bach.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance