En las dos primeras entradas de la serie Y tú, ¿cómo cuentas con los dedos? (parte 1 y parte 2) de la sección Matemoción del Cuaderno de Cultura Científica hemos hablado de algunas de las formas de contar con los dedos de las manos que se utilizan en la actualidad a lo largo de todo el mundo, algunas de las cuales tienen un origen muy antiguo.

La práctica de contar con los dedos de las manos es tan antigua como el propio origen de los números, seguramente hace más de cuarenta mil años. Cada pueblo fue desarrollando sus propias técnicas para contar utilizando sus manos, e incluso sus pies o partes de su cuerpo. Se contaron dedos, falanges, nudillos o las zonas entre los dedos, también se utilizaron diferentes posiciones de los dedos para expresar los diferentes números, se desarrollaron sistemas de numeración asociados con diferentes bases, como 5, 10, 12 o 20, entre otras, o se inventaron sistemas más artificiales como el chisanbop o la expresión digital de los números binarios.

Antes de entrar en el tema de hoy, expliquemos brevemente qué es eso de la expresión digital de los números binarios, que utilizan para contar algunas personas apasionadas de las matemáticas. Como se explica en este vídeo de Una de Mates, Los números binarios, todo número tiene una expresión binaria, como una serie de 1s y 0s, y toda expresión binaria se corresponde con un número en nuestro sistema de numeración decimal. Si tenemos en cuenta que cada posición en un número binario se corresponde con una potencia de 2 (1, 2, 4, 8, 16, 32, etcétera), al igual que en nuestra base decimal se corresponde con una potencia de 10 (unidades, decenas, centenas, unidades de mil…), entonces podemos conocer el valor, en nuestro sistema decimal, de una expresión binaria cualquiera sin más que conocer qué potencias de 2 están (cuando hay un 1) y cuales no (cuando hay un 0). Así, el número binario, de cinco dígitos, 11010 se corresponde con el número 1 x (2⁴) + 1 x (2³) + 0 x (2²) + 1 x (2¹) + 0 x (2⁰) = 1 x (16) + 1 x (8) + 0 x (4) + 1 x (2) + 0 x (1) = 26.

Podemos utilizar nuestras manos para realizar la expresión digital de los números binarios teniendo en cuenta que un dedo abierto simbolizará un 1 y un dedo cerrado un 0. Si utilizamos solo una mano, podremos representar del 0 al 31 mediante las expresiones binarias con cinco dígitos, cada uno de los cuales será un 1 o un 0, es decir, un dedo abierto o cerrado. Así, las potencias de 2 se expresarán digitalmente como: la mano cerrada es 0 (en expresión binaria 00000), solo el meñique abierto 1 (00001), solo el anular abierto 2 (00010), solo el corazón 4 (00100), solo el índice 8 (01000) y el pulgar 16 (10000), como se muestra en la siguiente imagen.

Y combinando los cinco dedos podemos representar todos los números entre 0 y 31. Como ejemplo se muestra la expresión digital de algunos números en la siguiente imagen. Si se utilizasen las dos manos, es decir, diez dedos, se podrían representar del 0 al 1023. Os planteo un pequeño juego “contad, en orden, los números del 0 al 31”.

En la entrada de hoy, tercera de la serie Y tú, ¿cómo cuentas con los dedos?, vamos a explicar un método muy antiguo que permitió contar hasta 10.000, pero más aún, hasta un millón, y cuyo uso estuvo muy difundido tanto en Occidente, como en Oriente, llegando a ser utilizado en muchas zonas hasta en época reciente. Esta forma de representar los números se utilizaba ya en el antiguo Egipto, aunque quienes sí la utilizaron ampliamente fueron los romanos, griegos, árabes, persas y estuvo muy difundida en Europa en la edad media y la moderna.

La primera publicación conocida en la que se recoge la explicación de este método de contar con los dedos fue la obra, escrita en latín, De temporum ratione (Sobre la división del tiempo), en su capítulo primero De computo vel loquela digitorum (Sobre la manera de contar y hablar mediante los dedos), del monje benedictino inglés Beda el Venerable (aprox. 672 – 735).

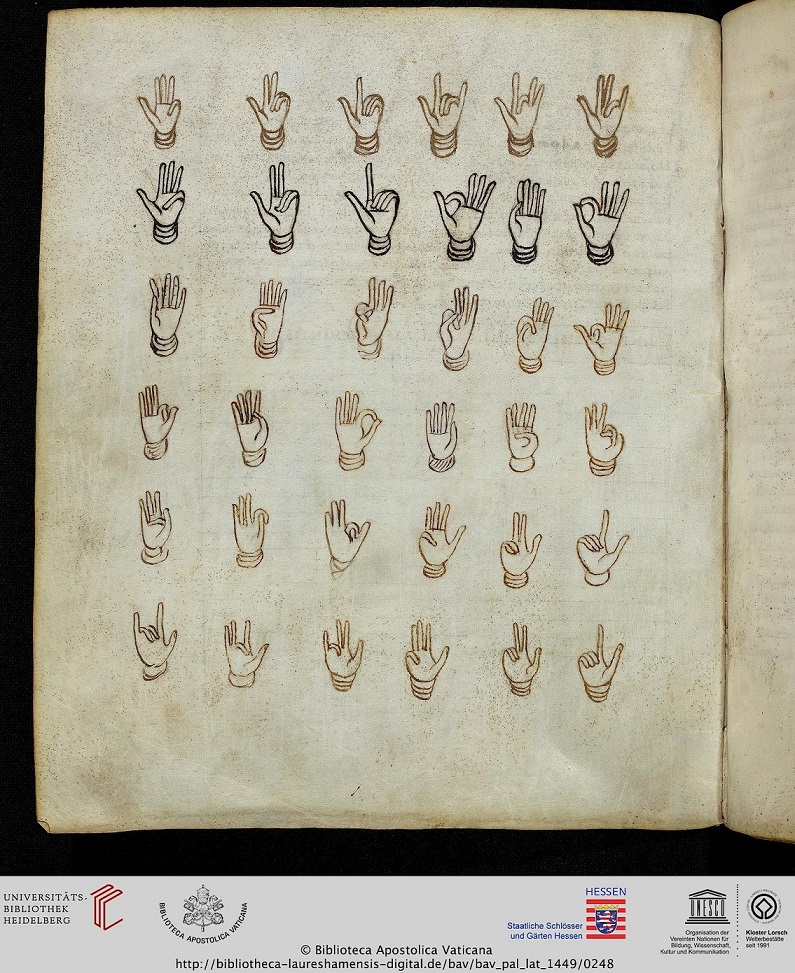
Beda inicia al primer capítulo De computo vel loquela digitorum de la obra De temporum ratione de la siguiente forma:

“Antes de que empecemos, con la ayuda de Dios, a hablar de cronología y su cálculo, consideramos necesario primero mostrar brevemente la muy necesaria y disponible técnica de contar con los dedos”.

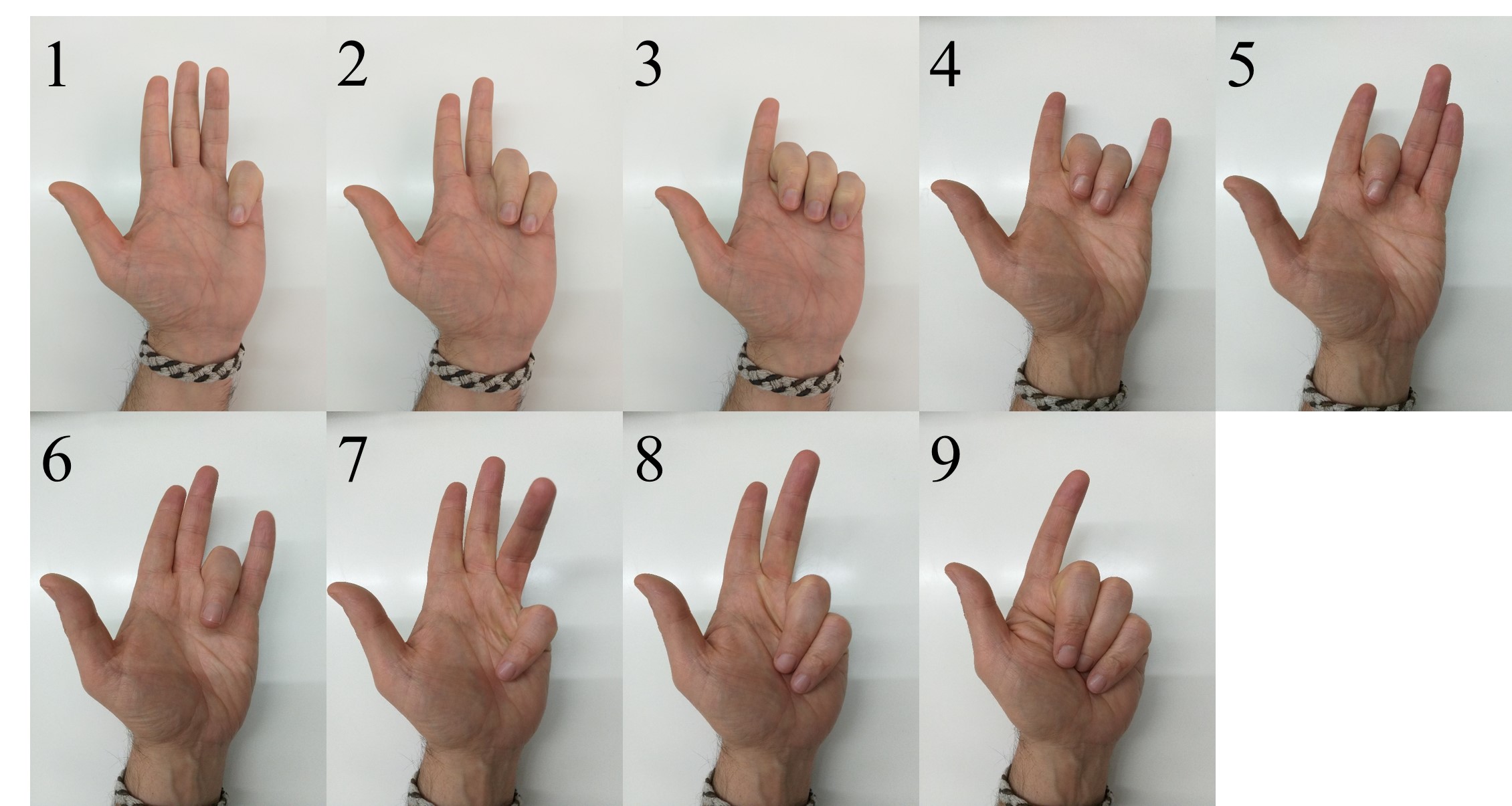
A continuación, el monje benedictino explica cómo hay que colocar los dedos de la mano izquierda para representar los primeros números. Veamos lo que está escrito para los números más pequeños, del 1 al 9, tanto en latín, como su traducción al castellano (pueden compararse los textos con la imagen que se incluye después de estos).

1 “Quum ergo dicis unum, mínimum in laeva digitum inflectens, in médium palmae artum infiges”

1 “Cuando digas uno, doblando el dedo pequeño (meñique) izquierdo, colócalo en la articulación media de la palma”

2 “quum dicis duo, secundum a minimo flexum ibídem impones”

2 “cuando digas dos, dobla el segundo dedo colocándolo en el mismo lugar”

3 “quum dicis tria, tertium similiter afflectes”

3 “cuando digas tres, pliega el tercero de la misma manera”

4 “quum dicis quatuor, ibidem minimum levabis”

4 “cuando digas cuatro, levanta el meñique de dicho lugar”

5 “quum dicis quinque, secundum a minimo similitier eriges”

5 “cuando digas cinco, levanta el segundo dedo de forma similar al meñique”

6 “quum dicis sex, tertium nihilominus elevabis, medio duntaxat solo, qui Medicus appellatur, in medium palmae fixo”

6 “cuando digas seis, levanta del mismo modo el tercero, manteniendo solo el llamado medicinal (anular) unido al centro de la palma”

7 “quum dicis sepiem, mínimum solum, caeteris interim levabis, super palmae radicem pones”

7 “cuando digas siete, levanta los demás dedos, mientras colocas el pequeño sobre la base de la palma”

8 “juxta quem, quum dicis octo, medicum”

8 “haz lo mismo, cuando digas ocho, con el medicinal”

9 “quum dicis novem, impudicum e regione”

9 “cuando digas nueve, añade el impúdico (el dedo corazón) al mismo lugar”

Como hemos podido leer, Beda llama minimum al dedo meñique, que era una de las formas de referirse al dedo pequeño de la mano. Por otra parte, según el Diccionario de la lengua española de la RAE, la expresión meñique es un “cruce de menino ‘niño’ y el dialectal mermellique o margarique, variantes de margarite, procedentes del francés antiguo margariz ‘renegado’, ‘traidor’, papel a veces atribuido a este dedo en dichos y consejas”. También se le conoce como dedo auricular, por la costumbre de hurgarse el oído (aurícula) con ese dedo, como ya menciona San Isidoro de Sevilla (556-636) en sus Etimologías (véase la cita en Antiquitatem).

El siguiente dedo, secundum, es el dedo anular, que Beda llama también medicus. Según San Isidoro de Sevilla se debe a que “con él aplican los médicos los ungüentos”, aunque varios autores lo relacionan con el hecho de que en la antigüedad se creía que existía una vena, llamada vena amoris (vena del amor), que conectaba directamente ese dedo con el corazón. Este podría ser el motivo por el cual ese es el dedo elegido para colocar el anillo de boda, y de ahí el otro nombre para ese dedo, el dedo anular. La costumbre de utilizar anillos de boda se remonta al Antiguo Egipto, de donde pasó a Grecia y Roma.

Existe otra explicación (véase, por ejemplo, el libro Number words and number symbols de Karl Menninger), conectada con la anterior, basada en el hecho de que los egipcios, que ya utilizaban esta práctica de contar con los dedos de las manos, representaban el número 6, como explica Beda, doblando el dedo anular. El número 6 es un número perfecto, por lo que en la antigüedad se consideraba un número divino, lo que hacía que el mencionado dedo tuviera un valor añadido, sobre los demás dedos, para ser elegirlo para colocar el anillo matrimonial. En matemáticas los números llamados perfectos son aquellos números que son iguales a la suma de sus divisores, por ejemplo, el 6 es un número perfecto (6 = 1 + 2 + 3) y también el 28 (= 1 + 2 + 4 + 7 + 14). Lo siguientes son 496 y 8128. Precisamente se les denominó “perfectos” por ese carácter mágico y divino que les atribuyeron en tiempos antiguos.

Al tercer dedo que menciona el monje inglés lo llama impúdico. Y ya lo explica San Isidoro de Sevilla en sus Etimologías, el motivo es “porque con frecuencia se expresa con él alguna burla infamante”. Ya entonces era, como lo sigue siendo hoy en día, el dedo utilizado para ese gesto obsceno que comúnmente se llama “sacar un dedo”, “hacer la peineta” o “hacer una peseta”, cuyo significado viene a ser algo así como “¡que te jodan!” o “¡que te den por culo!”. Este gesto ya era conocido en las antiguas Grecia y Roma. Por ejemplo, se encuentra en la comedia Las nubes [PDF] del dramaturgo griego Aristófanes (444 – 385 a.c.):

ESTREPSÍADES: ¿El digital? Por Zeus, ése lo conozco.

SÓCRATES: Pues dilo.

ESTREPSÍADES: Antes, cuando yo era niño, era éste de

aquí. (Levanta el dedo corazón)

SÓCRATES: Eres un patán y un imbécil.

Este dedo del que estamos hablando también se conoce con otros nombres, dedo medio, dedo mayor, dedo corazón, dedo cordial o digitus tertius (tercer dedo), por motivos obvios.

Volviendo al antiguo método de contar con los dedos descrito por Beda el Venerable en su libro De temporum ratione (Sobre la división del tiempo), hemos de destacar que, con tan solo tres dedos, el meñique, el anular y el corazón, de la mano izquierda, cuenta las unidades, del 1 al 9. Mientras que, como explicaremos ahora, con los otros dos dedos de esa misma mano, el índice y el pulgar, va a representar las decenas, 10, 20, así hasta 90, de forma que tan solo con la mano izquierda podrán representar todos los números entre el 1 y el 99.

Quizás se entienda un poco mejor con las explicaciones del propio monje, las primeras también en latín.

10 “quum dicis decem, ungem indicis in medio figes artu pollicis”

10 “cuando digas diez, coloca la uña del índice en la articulación media del pulgar”

20 “quum dicis viginti, summitatem pollicis inter medios indicis et impudici artus inmittes”

20 “cuando digas veinte, coloca la punta del pulgar entre el índice y el impúdico”

30 “cuando sigas treinta, junta en dulce abrazo el índice y el pulgar”

40 “cuando digas cuarenta, coloca el interior del pulgar sobre el lateral o el dorso del índice, con ambos dedos levantados”

50 “cuando digas cincuenta, inclina el pulgar hacia la palma, con la falange bajada al máximo, a semejanza de una letra griega  (gamma mayúscula)”

60 “cuando digas sesenta, dobla el pulgar como antes, con el índice envolviendo la parte que se encuentra ante la uña”

70 “cuando digas setenta, estando el índice como antes, es decir, envolviendo estrechamente la convexidad de la uña del pulgar, tendrá este la uña erguida hasta la articulación media del índice”

80 “cuando digas ochenta, estando el índice doblado como antes y el pulgar recto, coloca la uña de este (el pulgar) en la articulación media del índice”

90 “cuando digas noventa, coloca la uña del índice en la base del pulgar”

Para la descripción de las decenas, Beda utiliza los dedos índice y pulgar, que él llama indicis y pollicis. Respecto al índice, volviendo a las Etimologías de Isidoro de Sevilla, este dice así “El segundo [dedo] índice (index), y también salutaris o demonstratorius, precisamente porque con él saludamos o señalamos”. Efectivamente, este dedo se conoce con los nombres dedo índice (index) o dedo mostrador (demonstratorius), ya que es el que se utiliza para indicar, señalar o mostrar algo, y dedo saludador (salutaris).

Respecto al pulgar dice Isidoro de Sevilla “El primero se llama pulgar (pollex) porque entre los otros goza de poder (pollere) y potestad”. Según la RAE, el nombre de pulgar procede del nombre latino pollicaris, que a su vez viene de pollex, como lo llama Isidoro de Sevilla, quien ya nos da la idea de la procedencia de pollex, que no sería otra que la palabra latina pollere, poder. De pollicaris habría derivado a polgar y de ahí a pulgar. Además, el dedo pulgar también recibe el nombre de pólice, del mismo origen.

Este dedo también recibe el nombre de matapulgas o matapiojos, por ser el dedicado a tales fines. Así una de las variantes de una canción infantil donde se mencionan los cinco dedos dice así: “Este el chiquitillo, este el del anillo, este el de la mano, este el escribano, y este, el matapulgas y piojos de todo el año”. Hay quienes afirman, por ejemplo, el filólogo español Joan Corominas (1905-1997), autor del Diccionario crítico etimológico castellano e hispánico, que la “u” de pulgar derivó de la palabra pulga, que motivó el cambio de una “o” a una “u”. Hay quienes piensan que quizás el orden fue el inverso. De hecho, la RAE nos dice que pulga viene de la palabra latina pullex.

Al pulgar también se le denomina, dedo gordo.

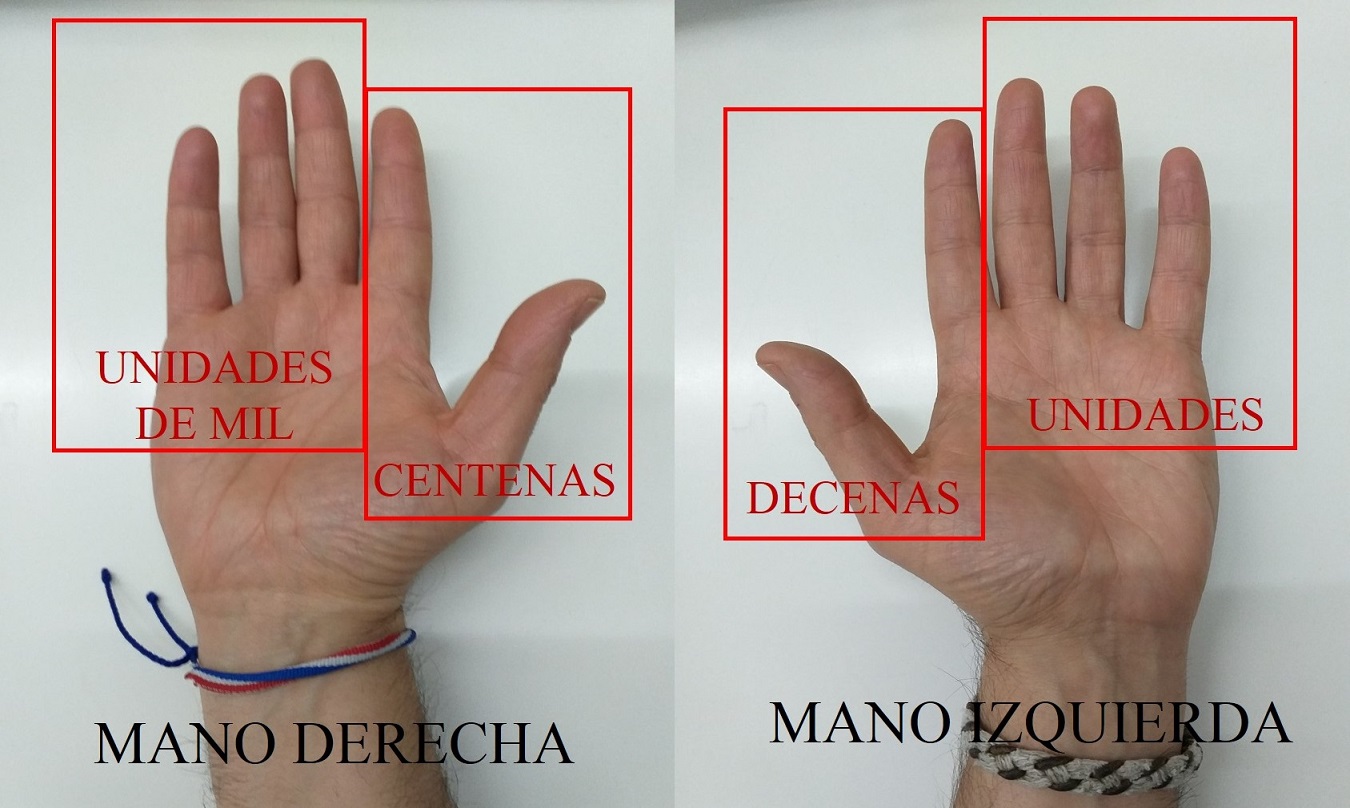
Pero sigamos con la descripción del método para contar números del 1 al 9.999. Como hemos comentado, los dedos meñique, anular y corazón de la mano izquierda se utilizaban para representar las unidades, mientras que los dedos índice y pulgar para representar las decenas. Por otra parte, para las centenas (100, 200, 300, …) se utilizaban los dedos índice y pulgar de la mano derecha, con los mismos signos que los descritos arriba con esos mismos dedos, pero de la mano izquierda. Mientras que los dedos meñique, anular y corazón de esa misma mano derecha se utilizaban, con los mismos gestos descritos para los de la izquierda, para representar las unidades de mil (1.000, 2.000, 3.000, …).

Así, si una persona, frente a nosotros, nos quiere representar un número de hasta cuatro cifras, levantará sus dos manos frente a nosotros, como se muestra en la imagen de abajo. Y podemos observar que esta forma de representar los números mediante los dedos de las manos es una representación posicional, similar a la que utilizamos nosotros en nuestro sistema de numeración moderno, puesto que el orden de las unidades, decenas, centenas y millares es de izquierda a derecha.

Veámoslo con un ejemplo concreto. Para representar con los dedos de las manos el número 2.539 se colocarán los dedos como se indica en la siguiente imagen.

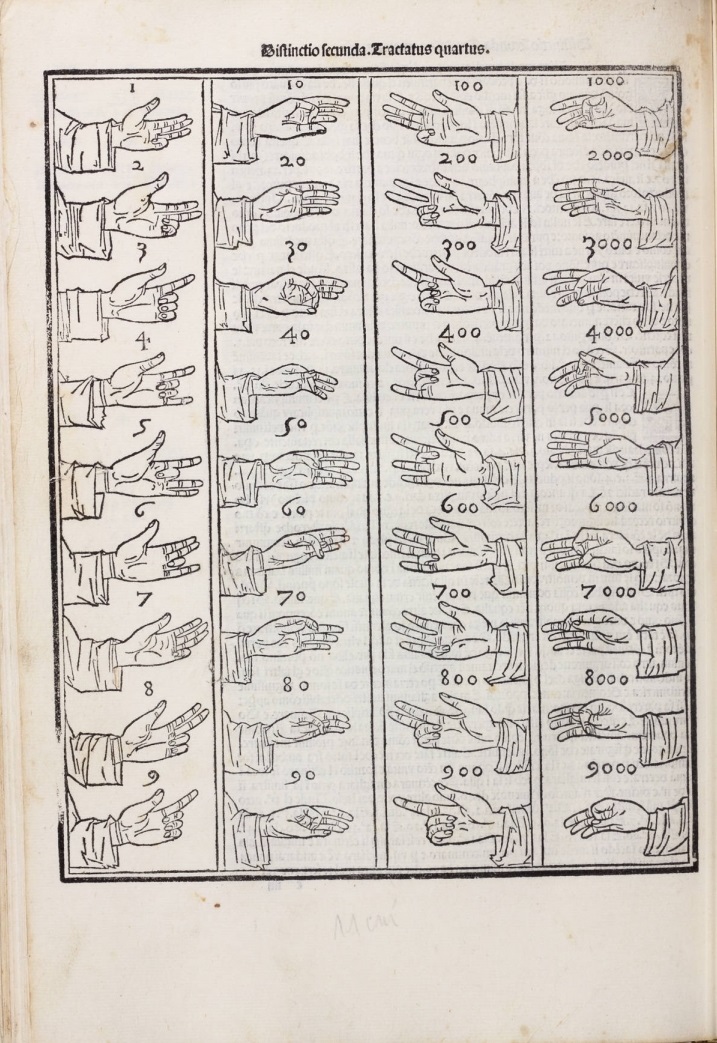
Pero el monje benedictino Beda el Venerable, que sería proclamado Doctor de la iglesia en 1899 por el papa León XIII, va más allá en el capítulo De computo vel loquela digitorum (Sobre la manera de contar y hablar mediante los dedos) explicando no solo cómo se puede contar hasta 10.000, sino hasta un millón. Para representar las decenas de mil se describen 9 posiciones diferentes de la mano izquierda respecto al cuerpo, de forma similar se utiliza la mano derecha para las centenas de mil.

En la obra Theatrum Arithmetico Geometricum (1727) del matemático, físico y fabricante de instrumentos alemán Jacob Leupold (1674-1727) se incluye una ilustración con el método de contar con los dedos de las manos que Beda recogía en su libro De temporum ratione.

Veamos las explicaciones del monje Beda para expresar las distintas decenas de mil (y que, más o menos, aparecen en la ilustración anterior):

10.000 “Para cuando digas diez mil, coloca el dorso de tu mano izquierda en medio del pecho con los dedos extendidos y apuntando al cuello”

20.000 “cuando digas veinte mil, coloca sobre el pecho la mano izquierda ampliamente extendida” [nota: En la ilustración de Leupold se expresa 20.000 de una forma diferente]

30.000 “cuando digas treinta mil, coloca la misma mano (hacia la derecha y de perfil) con el pulgar apuntando al cartílago central del pecho”

40.000 “cuando digas cuarenta mil, coloca el dorso de la mano sobre el ombligo”

50.000 “cuando digas cincuenta mil, manteniendo la misma posición, apunta con el pulgar de esa mano al ombligo”

60.000 “cuando digas sesenta mil, agarra el fémur izquierdo con esa mano siempre dirigida hacia abajo”

70.000 “cuando digas setenta mil, toca el mismo sitio con el dorso de la mano”

80.000 “cuando digas ochenta mil, coloca la mano sobre el fémur”

90.000 “cuando digas noventa mil, te tocas los riñones con la palma de la mano, con el pulgar apuntando hacia la ingle”

Para las centenas de mil, es decir, entre 100.000 y 900.000, se realiza la misma operación, pero en el lado contrario, es decir, con la mano derecha.

Teniendo en cuenta todos los gestos explicados hasta ahora, se pueden representar todos los números entre 1 y 999.999, aunque la verdad es que para los números muy grandes hay que hacer un verdadero ejercicio de contorsionismo con el cuerpo.

Finalmente, existe un símbolo para un millón, 1.000.000, que consiste en entrelazar los dedos de ambas manos.

Una descripción completa de este sistema para contar con los dedos de las manos, similar a la descrita por el monje inglés Beda en su libro De temporum ratione (725), nos la encontramos bastante lejos, tanto en el espacio como en el tiempo. Se trata del Farhangi Djihangiri, diccionario persa del siglo XVI, traducido al francés y comentado por el lingüista y orientalista francés Sylvestre de Sacy (1758-1838). La diferencia entre ambos textos está en que en el texto persa las unidades y decenas se representan con la mano derecha, mientras que se utiliza la izquierda las centenas y las unidades de mil, al revés que en el texto latino.

Existe una importante cantidad de textos y objetos que atestiguan el uso de esta técnica de contar con los dedos de las manos desde la antigüedad hasta hace relativamente poco tiempo. Para quienes puedan estar interesados, pueden encontrar una amplia información tanto en los mencionados libros de George Ifrah y Karl Menninger, como en los interesantes artículos Digital Reckoning among the Ancients, de Leon J. Richardson, y Numbers in the Greco-Roman World and the Early Middle Ages, de Burma P. Williams y Richard S. Williams.

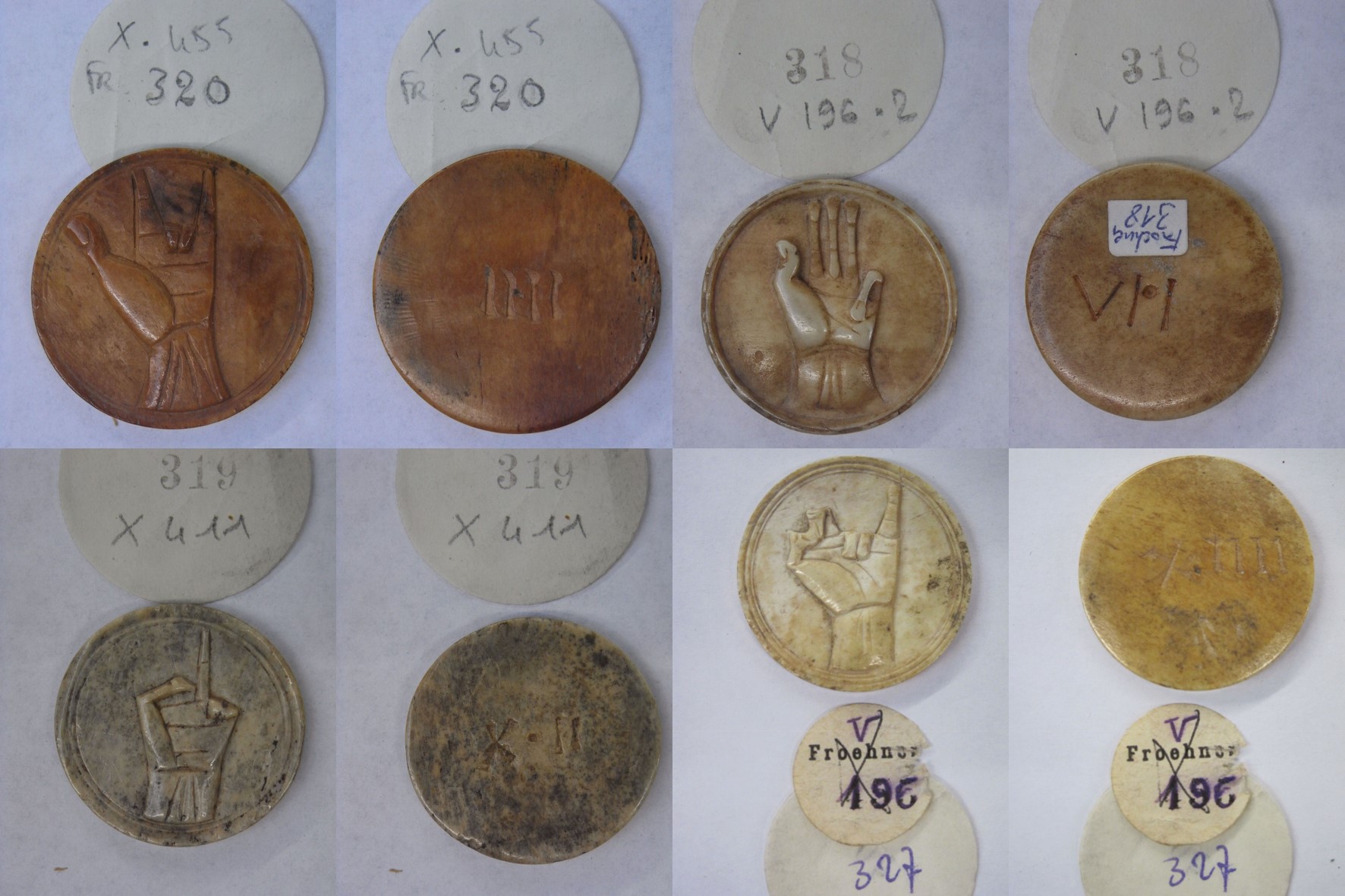
Aunque no podemos abordar aquí, por falta de espacio, estos significativos objetos y textos, al menos vamos a citar un ejemplo de cada conjunto de referencias. Por una parte, existen muchos ejemplos de téseras (según la RAE, “Tésera: pieza cúbica o planchuela con inscripciones que los romanos usaban como contraseña, distinción honorífica o prenda de un pacto”) romanas antiguas (aproximadamente, del siglo I a.c.), por ejemplo, en el Museo Británico (Londres), la Biblioteca Nacional de Francia (París) o el Museo Egipcio (El Cairo), en las cuales se puede observar en una de las caras un número romano, por ejemplo, el VII o el XIIII, y en la otra la forma en la que se representaba ese número con los dedos de las manos. Podemos especular sobre la función de estas téseras de marfil, aunque se desconoce cuál era realmente.

Los textos que he elegido para terminar esta entrada no son quizás los más significativos, pero los he elegido por estar relacionado con otro de los gestos de las manos. Me refiero al gesto relacionado con el hecho de que una persona sea tacaña, el puño cerrado. Se suelen utilizar expresiones del tipo “tiene el puño cerrado” o “es de la hermandad del puño cerrado”.

Algunos poetas árabes y persas relacionaban ser tacaño con el número 93, puesto que este se representa, según lo que hemos explicado en esta entrada, con la uña del índice izquierdo apoyada sobre la articulación inferior del dedo pulgar (para representar al 90) y los otros tres dedos, corazón, anular y meñique plegados (para representar el 3). Ese mismo gesto, pero en la mano derecha, sería el número 9.300. Por ejemplo, el poeta árabe Yahya ibn Naufal al Yamani (siglo VII) escribía

“Noventa seguido de tres, que un tacaño representa mediante un puño cerrado presto a golpear, no es tan miserable como tus dádivas, oh Yazid”

O el escritor, filólogo y gramático árabe Khalil ibn Ahmand (aprox. 718-791), que publicó el primer diccionario de la lengua árabe y fue uno de los fundadores de la poesía árabe, escribió

“Vuestras manos no han sido creadas para la generosidad, y su avaricia es notoria: una es 3.900 y la otra está tan desprovista de generosidad como un 100 al que le falta 7”

Y uno de los grandes poetas persas, Abu’l Kassim Firdussi (aprox. 940-1020), en su libro Shahnama o Libro de los reyes, que es una gran epopeya del mundo persa, ironiza sobre la avaricia del sultán Mahmud el Ghaznavida, diciendo

“La mano del rey Mahmud, de origen augusto, es nueve veces 9 y tres veces 4”

Bibliografía

1.- Página web de la artista Veera Pfaffli

2.- Jose Antonio Pérez (dirección), Raúl Ibáñez (guión), Los números binarios, Una de mates, Órbita Laika (TVE2) y Cátedra de Cultura Científica

3.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002 (quinta edición).

4.- Karl Menninger, Number words and number symbols, Dover, 1969.

5.- Página web de la Biblioteca Apostolica Vaticana

6.- Página web de la Bibliotheca Laureshamensis digital

7.- Diccionario de la lengua española de la RAE

8.- Antonio Marco Martínez, Antiquitatem, Los nombres de los dedos de la mano

9.- Public Delivery, Ai Weiwei gives world his middle finger

10.- Leon J. Richardson, Digital Reckoning among the Ancients, The American Mathematical Monthly, vol. 23, no. 1, pp. 7-13, 1916.

11.- Burma P. Williams, Richard S. Williams, Numbers in the Greco-Roman World and the Early Middle Ages, Isis, vol. 86, no. 4, pp. 587-608, 1995.

12.- Página web del fotógrafo Jim Marshall

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica