A diferencia de de las pelotas de tenis, las balas, y otras trozos de materia en movimiento, las ondas sí puden rodear una esquina. Por ejemplo, podemos oír una voz que viene desde el otro lado de una colina, a pesar de que no haya nada que refleje el sonido hacia nosotros. Estamos tan acostumbrados al hecho de que las ondas de sonido sean capaces de hacer esto que ni nos damos cuenta. Esta propagación de la energía de las ondas a lo que cabría esperar que fuese una región inaccesible se llama difracción. De nuevo, las ondas en el agua ilustran este comportamiento con mayor claridad. Seguro que ahora ves esta fotografía de otra manera.

La fotografía muestra uno de los casos en los que se produce difracción; en ella vemos que las ondas en el agua se difractan a medida que pasan a través de una estrecha ranura en una barrera. Añadamos que el tamaño de la apertura es menos de una longitud de onda de ancho. La onda aparece en la laguna y se propaga en todas direcciones. Si observamos el patrón de la onda difractada vemos que es básicamente el mismo patrón que establecería una fuente puntual de vibración si se coloca donde está la ranura apertura. Quizás lo veamos mejor con la ayuda de un esquema:

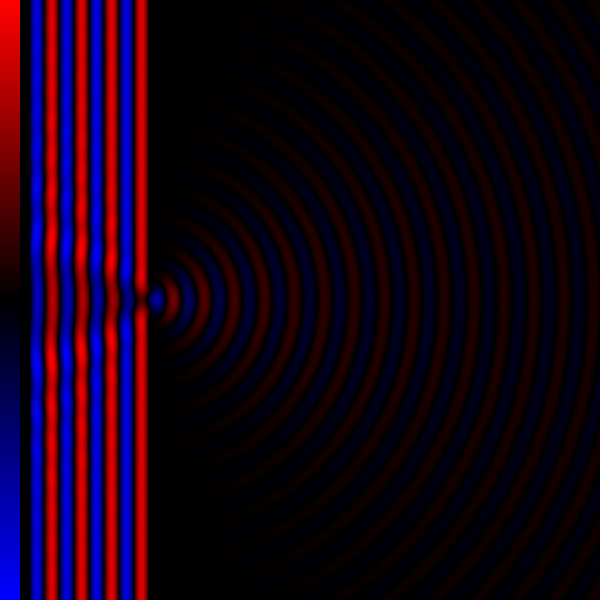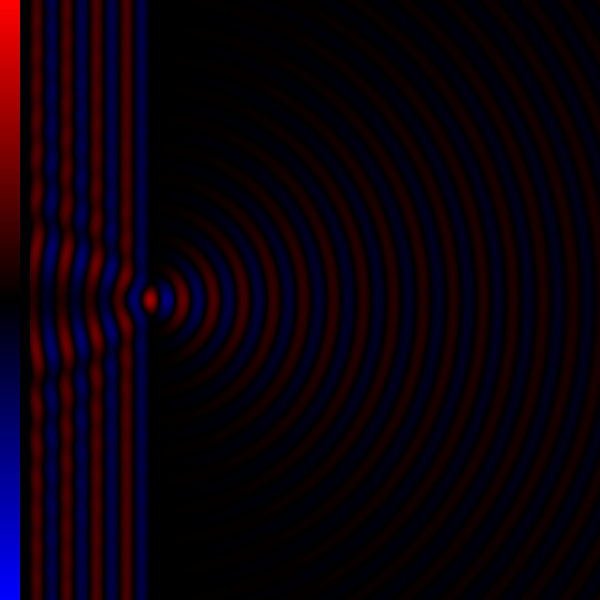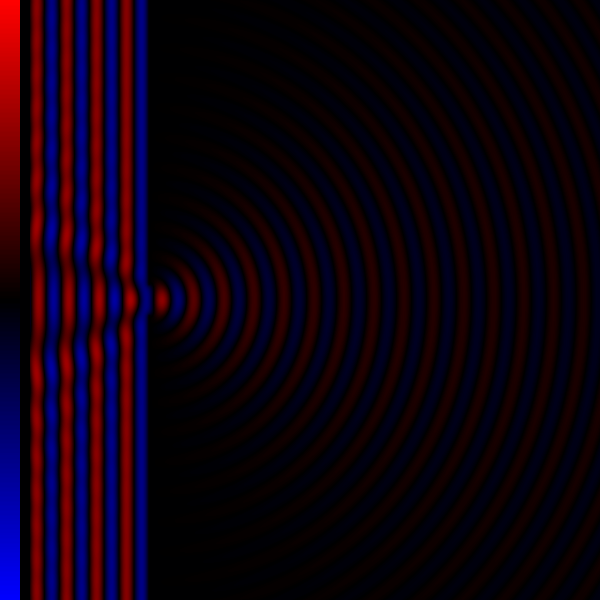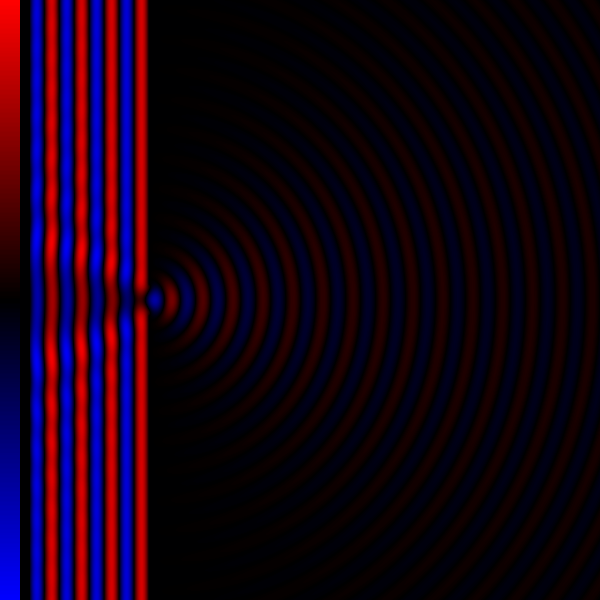
Veamos ahora la posibilidad de que, en vez de una, tengamos dos aperturas estrechas. De lo que hemos visto para una apertura cabe esperar lo que se observa realmente, esto es, que el patrón resultante que forman las ondas difractadas en ambas rendijas es el mismo que el producido por dos fuentes puntuales que vibran en fase. Así lo ilustró Thomas Young en su comunicación a la Royal Society al respecto en 1803:

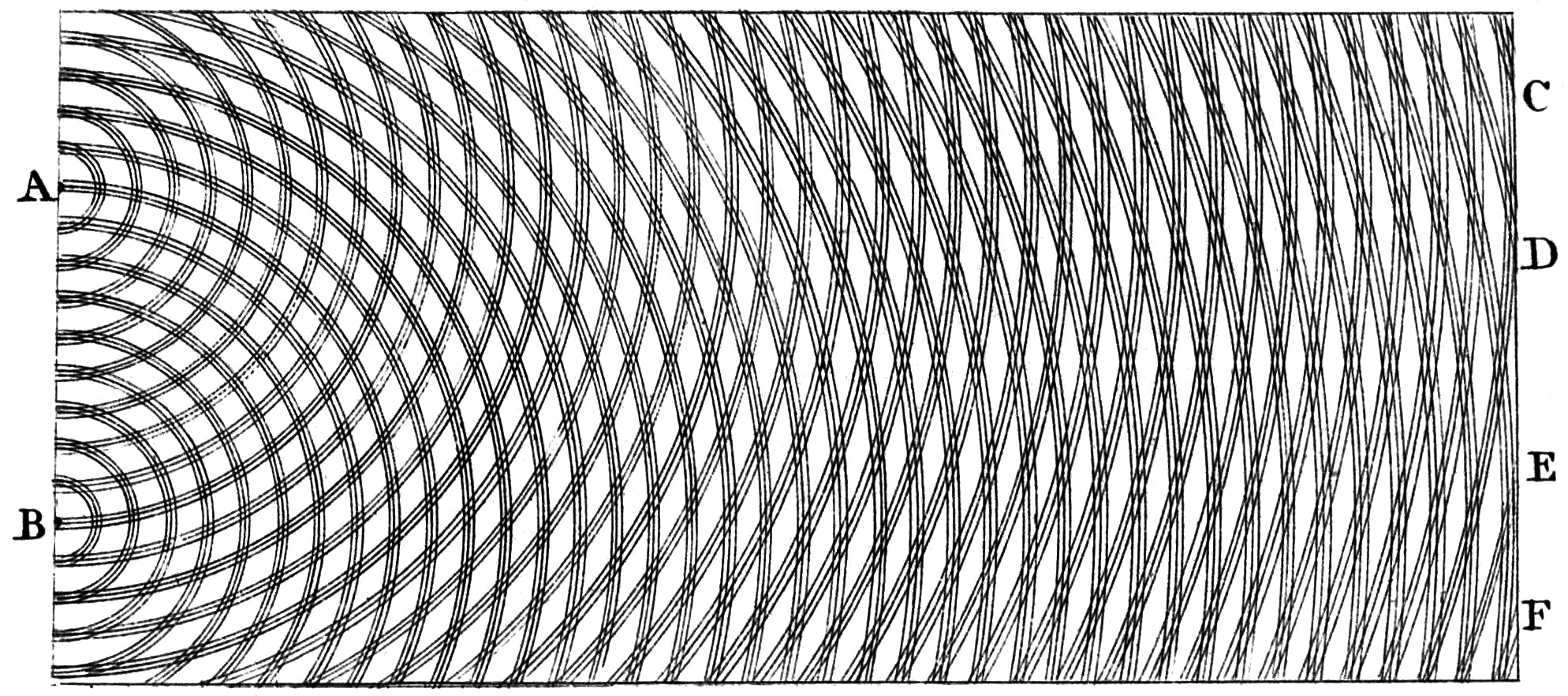
De forma general, si hay n aperturas estrechas (menores que una longitud de onda) en una barrera, el patrón de ondas observado después de la barrera se corresponde con el que habría en el medio si hubiese n fuentes puntuales en fase, cada una en la posición de una apertura.

Pero, ¿por qué ocurre esto?

Podemos describir estos y todos los demás efectos de la difracción a partir de una característica básica de las ondas. Esta característica se conoce como principio de Huygens, ya que la expresó por primera vez Christiaan Huygens en 1678. Necesitamos para entenderlo un concepto previo, el de frente de onda. Para una onda en el agua, un frente de onda es una línea imaginaria a lo largo de la superficie del agua, con cada punto a lo largo de esta línea exactamente en la misma fase de la vibración; es decir, todos los puntos de la línea están en fase. Dicho de otra manera y en general: un frente de onda es el lugar geométrico de todos los puntos adyacentes en los que la perturbación está en fase. Así, las líneas de cresta son frentes de onda, ya que todos los puntos de la superficie del agua a lo largo de una línea de cresta están en fase. Cada uno acaba de alcanzar su máximo desplazamiento hacia arriba, está momentáneamente en reposo, y comenzará a bajar un instante más tarde.

Como las ondas de sonido no se propagan sobre una superficie sino en tres dimensiones, sus frentes de onda no forman líneas sino superficies. Los frentes de onda para las ondas de sonido emitidas desde fuentes muy pequeñas son superficies casi esféricas, de la misma forma que los frentes de onda de las ondulaciones en el agua a partir de una fuente muy pequeña son círculos.

El principio de Huygens, puede expresarse así: cada punto de un frente de onda puede considerarse que se comporta como una fuente puntual de ondas generadas en la dirección de propagación de la onda original y con su misma velocidad y frecuencia. Traduciendo libremente a Huygens:

Existe la consideración adicional en la emanación de estas ondas de que cada partícula de materia en la que una onda se propaga, no debe comunicar su movimiento solamente a la siguiente partícula que está en la línea recta trazada desde la [fuente], sino que también impartirá algo de él necesariamente a todas las otras que la tocan y que se oponen ellas mismas a su movimiento. Así ocurre que alrededor de cada partícula se crea una onda de la que la partícula es el centro.

Seguiremos explorando las consecuencias del principio de Huygens en próximas entregas.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance