Una teselación o mosaico del plano consiste en una serie de polígonos –las teselas o losetas– que lo cubren sin dejar zonas vacías, de manera que si dos teselas se tocan, lo hacen necesariamente lado con lado o vértice con vértice.

En su obra Harmonice mundi el astrónomo Johannes Kepler estudió qué polígonos regulares podían cubrir el plano. Es decir, se preguntaba si existen mosaicos que utilicen un polígono regular como única tesela base. La respuesta es sencilla: los únicos que existen son los mosaicos por triángulos, cuadrados y hexágonos regulares.

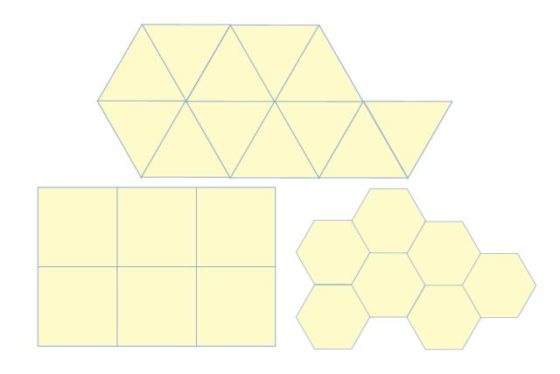
¿Por qué no hay más? Por ejemplo, en el caso del pentágono regular, su ángulo interno es de 108 grados. Si deseáramos teselar el plano con pentágonos regulares, los vértices de dos losetas colindantes deberían tocarse sin dejar ningún hueco. Pero esto imposible, ya que 360 no es divisible por 108. De otra manera, si colocamos pentágonos regulares alrededor de un vértice, se observa en seguida que solo pueden colocarse tres, pero queda un espacio que no puede cubrirse con pentágonos.

Recordemos que un polígono regular de n lados posee ángulos internos de 180(n-2)/n grados. Así, para polígonos con siete o más lados, el ángulo interior es mayor que 120 grados pero menor que 180, con lo que llegamos a la misma conclusión que con el pentágono. Es decir, el triángulo, el cuadrado y el hexágono (regulares) son los únicos polígonos regulares cuyos ángulos internos (60 grados, 90 grados y 120 grados, respectivamente) son divisores de 360 grados.

En el estudio de mosaicos podríamos proseguir preguntarnos qué sucede al mezclar varios polígonos regulares para cubrir el plano –teselaciones semirregulares, de estos solo hay ocho–, o al usar una única pieza no regular, o al utilizar varias no regulares. Estos problemas no son sencillos de resolver. Cuando su estudio comenzó a sistematizarse llevó al desarrollo de técnicas matemáticas complejas aplicadas al estudio de teselaciones del plano (y del espacio) que después han encontrado utilidad en otros campos.

Vamos a elegir uno de estos problemas tomando el pentágono como pieza clave. La pregunta que nos planteamos es: ¿se puede teselar el plano con un único pentágono (convexo) no regular? La respuesta es que se puede, y además existen solo quince maneras de hacerlo –parece casi seguro que esta es la cantidad, aunque está en fase de revisión–.

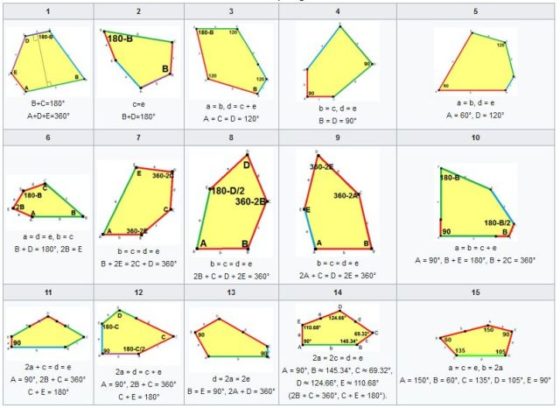
Citamos a continuación a las personas que han descubierto estas quince clases de pentágonos: Karl Reinhardt(1895-1941)encontró cinco en 1918 (ver [1]);Richard B. Kershner (1913-1982) halló tres más en 1968 (ver [2]); Richard James descubrió el noveno tipo en 1975 tras leer un artículo de Martin Gardner sobre teselaciones pentagonales en la revista Scientific American; ese artículo también inspiró a Marjorie Rice (1923-2017) quien halló otros cuatro tipos en 1976 y 1977 (ver [3] y [4]); Rolf Stein (ver [5]) encontró el decimocuarto tipo de pentágono en 1985; y en 2015 Casey Mann, Jennifer McLoud y David Von Derau descubrieron una nueva clase (ver [6]) con ayuda de un programa informático.

El 1 de mayo de 2017 Michaël Rao anunció (ver [7]) que había realizado una prueba asistida por ordenador en la que demostraba que estos quince pentágonos convexos eran los únicos que teselaban el plano con un único tipo de loseta. La parte computacional de su demostración ha sido revisada y no contiene errores, aunque aún no se ha publicado la prueba definitiva revisada por pares.

De este grupo de personas, algunas no son matemáticas. Richard James es informático y Marjorie Rice matemática aficionada. Ambos se enamoraron de este problema leyendo el artículo de Martin Gardner indicado anteriormente. Y emprendieron su búsqueda en solitario.

El caso de Marjorie es muy especial: aunque no tenía formación en matemáticas, desarrolló su propio sistema de notación para representar las restricciones y las relaciones entre los lados y ángulos de los pentágonos que estaba intentando encontrar. Fue la matemática Doris Schattschneider quien descifró la notación de Marjorie Rice y quien se ocupó de difundir sus descubrimientos entre la comunidad matemática. En la página Intriguing Tesselations, Marjorie Rice mostraba con orgullo sus descubrimientos y algunos mosaicos decorativos que diseñó a partir de ellos. ¡Admirable!

Referencias:

[1] Karl Reinhardt.Über die Zerlegung der Ebene in Polygone, Dissertation Frankfurt am Main (1918), páginas 77-81

[2] Richard Kershner. On paving the plane, American Mathematical Monthly 75 (8) (1968) 839-844

[3] Doris Schattschneider.Tiling the plane with congruent pentagons, Mathematics Magazine 51 (1) (1978) 29-44

[4] Marjorie Rice. Tesselations, Intriguing Tesselations

[5]Doris Schattschneider. A new pentagon tiler, Mathematics Magazine 58 (5) (1985) 308

[6] Casey Mann, Jennifer McLoud-Mann, David Von Derau, Convex pentagons that admit i-block transitive tilings. arXiv:1510.01186(publicado posteriormente en Geometriae Dedicata 194 (2018)141-167)

[7] Michael Rao.Exhaustive search of convex pentagons which tile the plane. arXiv:1708.00274

[8] Natalie Wolchover. Pentagon Tiling Proof Solves Century-Old Math Problem. Quanta Magazine, 11 julio 2017

[9] Pedro Alegría. El caso de los 14 pentágonos que embaldosan un espacio infinito. ABC Ciencia, 10 abril 2017

[10] Teselados pentagonales, Wikipedia [consultado 15 febrero 2020]

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.