Una de mis pasiones, como ha quedado reflejado en muchas de mis entradas del Cuaderno de Cultura Científica, es el arte contemporáneo y, en particular, su relación con las matemáticas.

Durante todos estos años, he escrito sobre el teorema de Pitágoras en la obra de muchos artistas contemporáneos (véase la entrada El teorema de Pitágoras en el arte), sobre cómo algunos artistas han utilizado los números primos para generar piezas artísticas (véanse las entradas El poema de los números primos y El poema de los números primos (2) sobre la obra de la artista donostiarra Esther Ferrer, o Los ritmos primos de Anthony Hill, sobre una obra del artista británico Anthony Hill), de la inspiración artística de un rompecabezas geométrico como el tangram (véase El arte contemporáneo mira al tangram), sobre la utilización de la superficie de una sola cara conocida como banda de Moebius (véase Arte Moebius (I) y Arte Moebius (II)), de la normalidad del número pi en la obra Pi (2009-2010), de la artista Esther Ferrer (véase ¿Es normal el número pi?), entre otros conceptos, objetos y resultados matemáticos.

En esta entrada estamos interesados en cómo algunos conceptos matemáticos abstractos, como es el concepto de grupo abstracto y, relacionado con el mismo, el concepto de cuadrado latino, son una interesante herramienta de creación artística en el arte contemporáneo. Esto ya lo pusimos de manifiesto en la entrada Cuadrados latinos, matemáticas y arte abstracto, en la que hablamos de uno de los artistas cuyo arte se enmarca dentro del constructivismo y el arte concreto, el pintor y artista gráfico suizo Richard Paul Lohse (1902-1988).

Un bonito ejemplo es la obra del artista constructivista estadounidense John Ernest (1922-1994), titulada Iconic Group Table, de alrededor de 1978, que vamos a explicar a lo largo de esta entrada.

Vayamos por partes. Primero recordemos los conceptos matemáticos relacionados con esta obra, en particular, el concepto de grupo abstracto.

Un grupo es un conjunto, llamémosle G, con una operación *, de modo que a partir de dos elementos a y b del conjunto G, nos da un nuevo elemento, a * b, del conjunto G, y tal que dicha operación verifica una serie de axiomas:

i) propiedad asociativa, a * (b * c) = (a * b) * c, para todos los elementos a, b y c de G;

ii) elemento identidad, existe un elemento e de G tal que a * e = a = e * a;

iii) elemento inverso, para cada elemento a de G, existe un elemento b (llamado inverso, y que suele denotarse como a^–1) tal que a * b = e = b * a. Los grupos son abelianos si se cumple la propiedad conmutativa, es decir, si para cualesquiera elementos a y b de G, a * b = b * a, pero no todos los grupos son abelianos.

Dos ejemplos cotidianos de grupos, en el sentido de que los manejamos en nuestro día a día, son los números enteros Z con la operación suma +, o los números reales R con la operación producto x.

El matemático inglés Arthur Cayley (1821-1895), del que se puede leer en el libro Cayley, el origen del álgebra moderna (RBA, 2017), describía la estructura de los grupos finitos (es decir, con un número finito de elementos) mediante la tabla de los productos de los elementos del grupo, la llamada tabla de Cayley, en la que se colocan a la izquierda y arriba de la tabla los elementos del grupo y en las casillas correspondientes (como en el juego de los barcos) se sitúa el producto de los mismos.

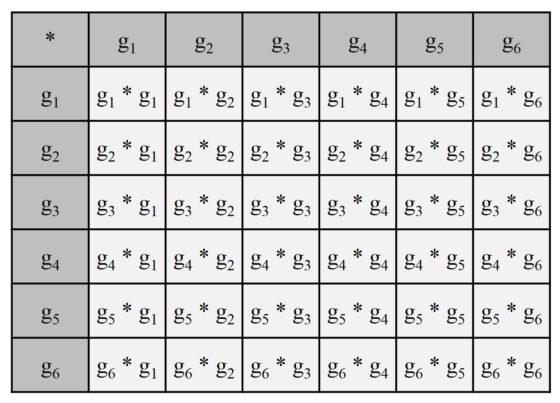
Veamos, por ejemplo, la tabla de Cayley de un grupo finito de seis elementos.

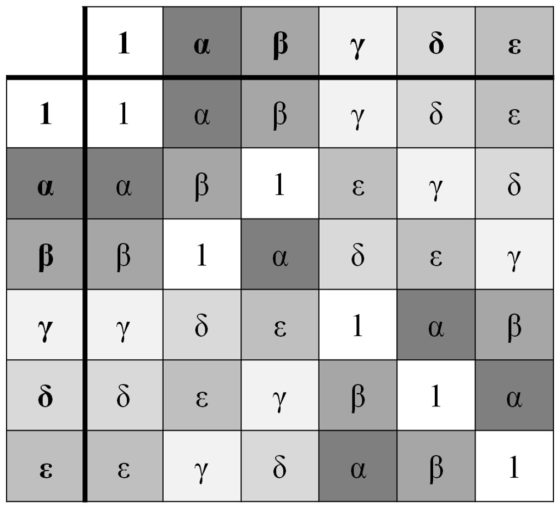
La tabla de Cayley de un grupo de n elementos realmente sería la tabla de tamaño n x n con todos los productos posibles entre los elementos del grupo, sin tener en cuenta ni la primera fila (por arriba), ni la primera columna (por la izquierda), que ya aparecen en la tabla interior en la fila y columna correspondientes al elemento identidad (en el ejemplo anterior tenemos una tabla 6 x 6, donde la primera fila y columna se corresponden efectivamente con el elemento identidad 1).

Aunque el ejemplo de grupo abstracto que genera la obra Iconic Group Table es muy interesante e ilustrativo, como puede verse más abajo.

A continuación, recordemos el concepto de cuadrado latino. Un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n (aunque bien podrían considerarse n símbolos cualesquiera, por ejemplo, las letras del alfabeto latino que utilizó el matemático suizo Leonhard Euler o los colores utilizados por Lohse), de tal forma que cada número de {1,…, n} aparece una vez, y sólo una vez, en cada fila y cada columna.

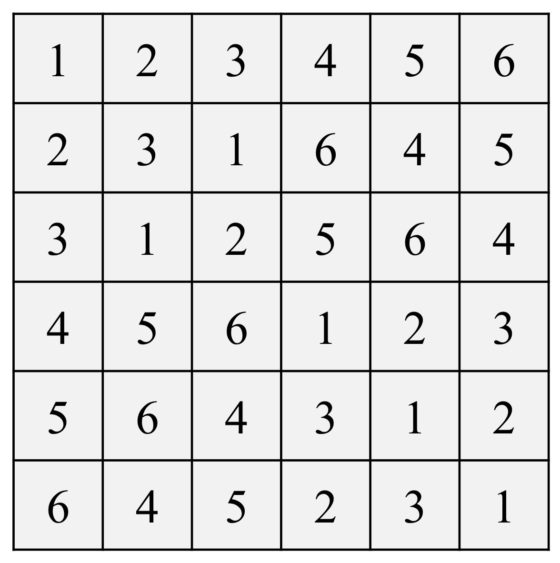
Las propiedades del grupo abstracto hacen que la tabla de Cayley de los grupos finitos sean cuadrados latinos de orden igual al número de elementos del grupo. La explicación matemática es esta: si G = {g₁, g₂,…,g_n} y si en una fila, por ejemplo, la del producto del elemento g_k apareciese un mismo elemento en dos entradas (que es lo que ocurriría si no fuese un cuadrado latino), entonces existirían dos elementos distintos del grupo, g_i y g_j, tal que g_k * g_i = g_k *g_j (los valores de las dos entradas), y multiplicando por la izquierda por el inverso de g_k, tendríamos que g_i = g_j, lo cual no es posible ya que los elementos g_i y g_j son distintos. Y lo mismo para las columnas.

Por ejemplo, el cuadrado latino de la imagen anterior es el que se corresponde con el grupo de seis elementos que habíamos mostrado más arriba, donde el 1 es la unidad (1) del grupo, el 2 es el elemento α, el 3 es el elemento β, el 4 es el γ, el 5 es el elemento δ y el 6 es el elemento ε. De esta forma la tabla de Cayley del grupo de seis elementos es exactamente el cuadrado latino mostrado, como puede observarse.

Pero vayamos ya con la parte artística de esta entrada del Cuaderno de Cultura Científica, la obra titulada Iconic Group Table, de John Ernest, y su relación con la teoría de grupos.

John Ernest (1922-1994) fue un artista estadounidense afincado en Inglaterra desde 1951. Se convirtió en miembro del grupo de los constructivistas británicos (también conocidos como construccionistas) junto a artistas como Victor Pasmore, Kenneth Martin, Mary Martin, Anthony Hill, Stephen Gilbert y Gilliam Wise, y posteriormente, estuvo relacionado con el Grupo Sistemas –Systems group–, interesado en formas de arte sistemáticas y matemáticas.

En un artículo de 1961 para la revista Structure, John Ernest escribió algo así:

“Supongo que estoy tratando de conseguir parte de la belleza de un sistema matemático formal en una experiencia visual, porque es este tipo de belleza en las matemáticas –donde la hermosa maquinaria abstracta entra en acción– lo que me conmueve más profundamente”.

O también, en el catálogo de la exposición Four Artists Reliefs, Constructions and Drawings, que tuvo lugar en el Victoria and Albert Museum de Londres, en 1968, escribió:

“Me gusta hacer cosas en las cuales los elementos sean distintos y en las que cada decisión sea segura e inequívoca. Mis elementos son cuadrados, triángulos, líneas y otras formas simples. Sus propiedades de color y distintas cualidades de superficies, junto con otras cuestiones como los niveles de relieve, la distancia entre los elementos, etc. constituyen mi paleta. Principalmente trabajo combinando estos elementos – tanto de forma material o en mi mente. Yo organizo y reorganizo mis elementos básicos hasta que haber configurado un montaje que me complazca o que satisfaga mis condiciones previas de trabajo.

Dos intereses principales subyacen en mi trabajo. Uno es el medio físico del relieve mismo y el otro es mi interés por las estructuras matemáticas. Pueden ser fundamentalmente diferentes, pero no son incompatibles. Me parece a mí que la separabilidad de las partes del relieve proporciona una contraparte física a los conjuntos de elementos de un sistema matemático. Sin embargo, los dos intereses rara vez se equilibran en una sola obra. Los relieves que tengo en esta exposición muestran un sesgo hacia la explotación de propiedades físicas (la excepción es el “relieve lineal 1” que intenta ser ingenioso sobre la reflexión bilateral). Los dibujos están estructurados de manera más rigurosa y originalmente se diseñaron como análogos visuales de tablas de grupos particulares.”

Como decíamos al principio de esta entrada, la obra de John Ernest que nos interesa es Iconic Group Table, de alrededor de 1978, que es un ejemplo contundente del uso del concepto de grupo abstracto como herramienta de creación artística.

La parte elevada y destacada de la pieza, que es de un tamaño importante, recuerda a un tablero de ajedrez de tamaño 8 x 8. Y es precisamente ese tablero central el que ilustra una tabla de Cayley de un cierto grupo abstracto con ocho elementos, que mostraremos a continuación, con una operación de grupo que es la “diferencia simétrica” de la teoría de conjuntos.

Para empezar, mostremos los ocho elementos que componen este grupo, que son ocho elementos geométricos, los ocho cuadrados siguientes, de base blanca con un trazado geométrico negro dentro. En realidad, John Ernest utilizó trazos curvos, mientras que yo he considerado trazos rectos en esta reproducción de sus elementos.

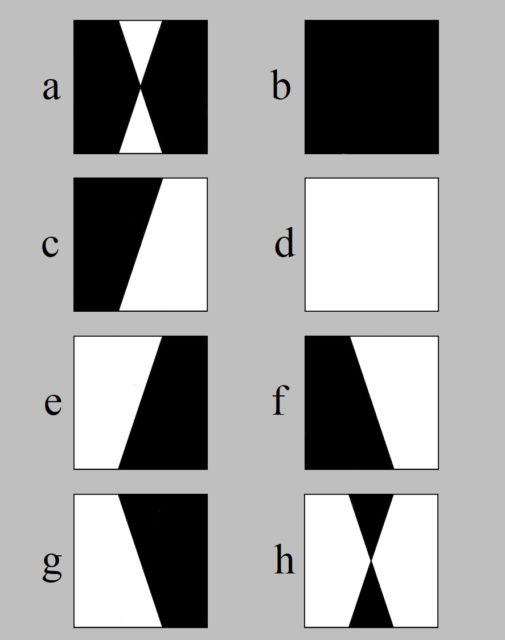
La operación es la diferencia simétrica de la teoría de conjuntos. La diferencia simétrica de dos conjuntos es la unión de los conjuntos menos su intersección. Es decir, dados dos conjuntos A y B, su diferencia simétrica es A ∪ B – A ∩ B. Si tenemos en cuenta que la zona negra de cada diseño es “nuestro conjunto” en cada elemento, veamos cómo se realiza la diferencia simétrica en dos casos distintos.

Por lo tanto, la tabla de Cayley para el grupo formado por los anteriores ocho elementos (a, b, c, d, e, f, g, h), con la operación diferencia simétrica es la siguiente.

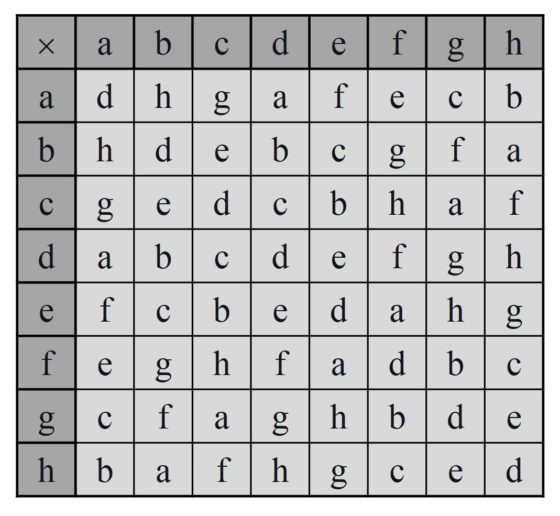
El elemento d es la identidad del grupo (a x d = a, b x d = b, …) y todos los elementos del grupo son de orden 2, es decir, multiplicados por sí mismos da la identidad (a x a = d, b x b = d, …).

La parte que representa el artista John Ernest en esta obra es la tabla de Cayley, es decir, la 8 x 8 correspondiente a las operaciones del grupo. Aunque ha cambiado el orden de las filas como aparece indicado en la siguiente imagen.

Podéis comprobar que la obra Iconic Group Table se corresponde con la tabla de Cayley de la estructura de grupo abstracto que hemos definido arriba, pero con el cambio en el orden de las filas que acabamos de indicar.

Para terminar con esta estructura, podríamos dar el cuadrado latino asociado a la tabla de Cayley de este grupo abstracto. Para empezar, quedémonos con la parte correspondiente a los resultados de los productos entre los elementos del grupo, es decir, la tabla 8 x 8, y pintemos las casillas de colores en función del elemento que está en la misma.

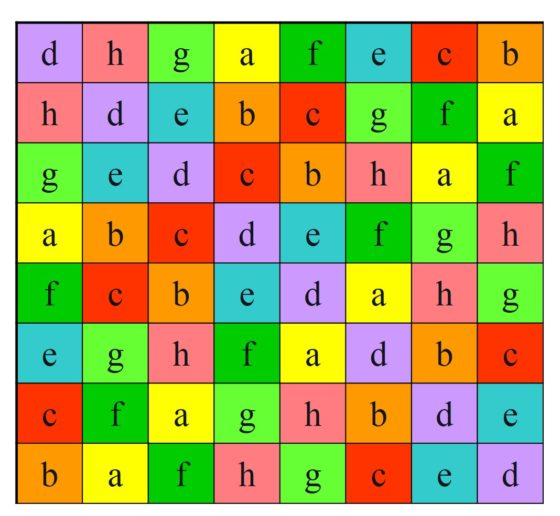
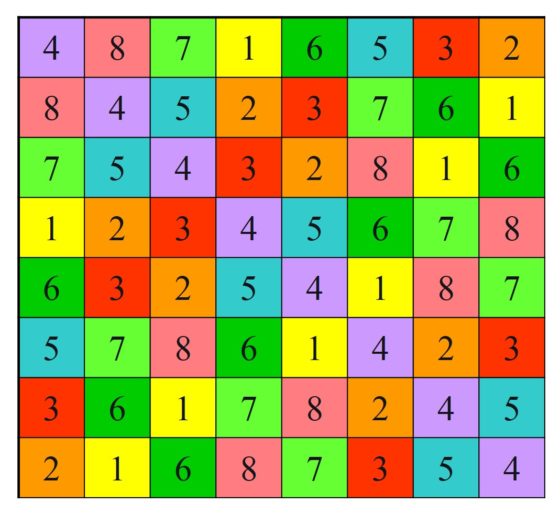
Y, por último, sustituyamos las letras por números: a es 1 (amarillo), b es 2 (naranja), c es 3 (rojo), d es 4 (violeta), e es 5 (azul), f es 6 (verde oscuro), g es 7 (verde claro) y h es 8 (rosa). Es un cuadrado latino de orden 8.

Otra obra de John Ernest con una construcción similar es Borromean rings (1971).

Cerramos esta entrada del Cuaderno de Cultura Científica con un par de obras más del artista John Ernest.

Bibliografía

1.- Raúl Ibáñez, Cayley, el origen del algebra moderna, RBA, 2017.

2.- Paul Ernest, John Ernest, A Mathematical Artist, Philosophy of Mathematical Education Journal, Number 24, 2009.

3.- Alan Fowler, A Rational Aesthetic, Philosophy of Mathematical Education Journal, Number 24, 2009.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica