El año 2013 dedicamos tres entradas del Cuaderno de Cultura Científica a una interesante propuesta musical del grupo estadounidense de música indie rock Artichoke. Esta consistía en dos álbumes, 26 scientists, volume one, Anning-Malthaus (BMI 2005) y 26 scientists, volume two, Newton-Zeno (BMI 2009), en los que en cada canción se realiza una pequeña reseña biográfica de un científico o científica. Algunos de los científicos a los que el grupo Artichoke dedicó una canción biográfica son la paleontóloga Mary Anning, la física y química Marie Curie, el naturalista Charles R. Darwin, el físico Albert Einstein, el astrónomo y matemático Galileo Galilei, el físico y matemático Isaac Newton, el médico y fisiólogo Ivan P. Pavlov o la bióloga Jeanne Villepreux, entre otros. Aquí podéis leer estas tres entradas y escuchar las canciones que componen los dos álbumes, 26 scientists:
A. 26 Científicos (Artichoke) (I): Anning/Ingenhousz
B. 26 Científicos (Artichoke) (II): Jefferson/Pavlov
C. 26 Científicos (Artichoke) (y III): Quine/Zeno
El objetivo de esta entrada es realizar un pequeño paseo por algunas canciones, de grupos de diferentes estilos musicales, dedicadas a objetos matemáticos, como los números primos, la sucesión de Fibonacci, el número Pi o el conjunto de Mandelbrot.
Como comento en mi último libro La gran familia de los números (Catarata, 2021), “los números primos son, sin lugar a dudas, la familia de números naturales más importante de la aritmética”. La importancia y trascendencia de estos números es tal que han llegado a calar incluso en la cultura. Nos los podemos encontrar en el arte, como en las series de obras Poema de los números primos y Un mar de números primos de la artista donostiarra Esther Ferrer (véanse las entradas El poema de los números primos, El poema de los números primos (2) o el libro La gran familia de los números) o la obra Ritmos primos del artista británico Anthony Hill (véase la entrada Los ritmos primos de Anthony Hill); en la literatura, como en la mítica novela Contacto (1985), del astrónomo y divulgador científico estadounidense Carl Sagan (véase la entrada Buscando lagunas de números no primos), la novela de humor Los humanos (2014), del británico Matt Haig o La soledad de los números primos (2008), del escritor italiano Paolo Giordano; en los comics, como en Prime Suspects, the Anatomy of Integers and Permutations (2019), de Andrew Granville, Jennifer Granville y Robert J. Lewis; e incluso en la música como vamos a mostrar con el siguiente ejemplo.
La canción que vamos a comentar a continuación, cuyo título es precisamente Prime numbers (números primos), pertenece al álbum Great Calamities (2006) del dúo musical The Two Man Gentlemen Band. El estilo de este moderno dúo musical es una mezcla de jazz, swing y vodevil con letras humorísticas, al estilo del grupo de los años 1930 y 1940, Slim & Slam.

Antes de nada, hay que escuchar la canción. Podéis hacerlo aquí: Prime Numbers de The Two Man Gentlemen Band. Como vemos, en esta versión en directo empiezan con cierta guasa.
Vayamos con la letra de la canción. La primera estrofa dice así:
Last night, as my baby was sleepin’ inside her bed, // I took a tape measure to her, just to see what it read. // Said «37» ‘round her bosom, and «29» around her waist, // Said «37» ‘round her hips, and I began to celebrate.
Algo así como “Anoche, cuando mi chica estaba durmiendo en su cama, cogí una cinta métrica para medirla, solo para ver qué medidas tenía. Midió 37 de pecho y 29 de cintura, midió 37 de caderas, y empecé a celebrarlo”. [*]
Después sigue el coro:
My baby’s got prime numbers. Prime numbers, oo-ee! // That means she’s only divisible by one // And that one’s gonna be me.
Que podríamos traducir como “Mi chica tiene números primos. Números primos, ee-oo! Esto significa que ella solo es divisible por uno y que ese uno voy a ser yo”.
La siguiente estrofa de la canción dice:
I once knew a girl in Boston. She had nice round and curvy hips. // I took a look at her brassiere, it said she was a 36 // It was then my heart was broken, for I knew she wouldn»t be all mine. // I’d have to split her up with other fellas: 2, 3, 4, 6, 12, 18, or 9.
Cuyo significado es algo así como “Una vez conocí una chica en Boston. Ella tenía unas bonitas caderas, redondas y voluptuosas. Eché un vistazo a su sujetador y observé que tenía 36 de pecho. Entonces se me rompió el corazón, porque sabía que ella nunca sería del todo mía. Tendría que compartirla (dividirla) con otros tipos: 2, 3, 4, 6, 12, 18 o 9”.
Los autores de esta canción están jugando con el concepto de número primo. Un tal número es aquel que solo es divisible por uno, además de por sí mismo, como lo son el 29 y el 37 de la canción. Sin embargo, el 36 no es número primo ya que, además de por sí mismo y por uno, es divisible por 2, 3, 4, 6, 9, 12 y 18. Hay personas, como el protagonista de esta canción, a quienes les fascinan los números primos y “juegan” a buscarlos en su vida a diario. Aunque, el protagonista de este tema le da demasiada importancia a los mismos, ya que valora el éxito o fracaso de su relación con las mujeres en función de si “miden números primos”.

Vamos a incluir otra canción relacionada con los números primos. Hace unos años descubrí un curioso grupo que se autodefinía, en su página de Facebook, como “un grupo de punk rock escéptico con una doble misión: por una parte, dar a conocer las maravillas de la ciencia de forma accesible y entretenida, por otra refutar supersticiones y creencias pseudocientíficas”. Entre los temas de su único disco PDP-1 (2011) nos encontramos Evoluciona, Calculadora, Kurt Gödel, Colisionador, Radiaciones, Heisenberg, Homeopatía, Doble ciego, Mecánica cuántica, Efecto 2000, PDP-1 y la que nos interesa escuchar hoy, Números primos.
Podéis escuchar la canción Números primos en YouTube o en bandcamp.
La letra de esta canción punk es la siguiente:
Eres un uno, un dos, un tres, un cinco y un siete. // Eres un once, un trece y un diecisiete. // Eres un diecinueve y un veintitrés. // Eres un primo pero no lo ves. // Desde hace tiempo, el factorizarte // nadie sabe bien si es P o NP. // Eso de dividirte no sabes lo que es. // Eres un primo pero no lo ves.
De nuevo nos encontramos con una canción sobre los números primos. La primera estrofa de cuatro versos nos habla en general de los números primos, poniendo algunos ejemplos, los nueve primeros números primos: 2, 3, 5, 7, 11, 13, 17, 19 y 23. En la segunda estrofa nos habla del problema de factorizar cualquier número natural como producto de números primos. El teorema fundamental de la aritmética nos dice que todo número natural puede expresarse, de forma única, como producto de números primos. Así, 6 = 2 x 3, 36 = 2 x 2 x 3 x 3 o 223.092.870 = 2 x 3 x 5 x 7 x 11 x 13 x 17 x 19 x 23. Pero aquí nos encontramos con dos problemas relacionados de una gran complejidad, el problema de saber si un número natural es primo o complejo, y en este segundo caso, el problema de factorizar dicho número como producto de números primos.
El siguiente objeto matemático en el que nos vamos a fijar es la sucesión de Fibonacci, que empieza así 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc. y que cada término es igual a la suma de los dos anteriores. En el cuaderno hemos hablado en varias ocasiones de esta sucesión, como en las entradas Póngame media docena de fibonaccis, El origen poético de los números de fibonacci o Nos encanta fibonacci, de mi compañera Marta Macho, pero también en mi conferencia El teorema de la rosa.
La propuesta musical relacionada con este objeto matemático es la siguiente, Fibonacci sequence (2001), de Dr. Steel, que podéis escuchar en YouTube.

Un par de apuntes sobre el Dr. Steel. Es un curioso músico norteamericano que siempre aparece caracterizado de científico loco (bata blanca, guantes de goma negros y gafas negras), con un conjunto de músicos-robots (cuando ha tocado en directo con un grupo real se ha justificado diciendo que los robots se habían estropeado). Su música ha sido definida como “opera hip-hop industrial” o también “steampunk”. Se muestra como un visionario, que va a dominar el mundo para crear su mundo utópico. Ha creado a su alrededor un grupo de seguidores que se denomina “Army of the Toy Soldiers” que ayudarán al Dr. Steel a dominar el mundo.
Como se ve en el video de youtube anterior, la canción es un poco loca, con una letra en el mismo sentido. La parte más relacionada con la sucesión de Fibonacci es la parte del coro, que dice así:
“(0) // Make me (one) // Copy and paste. Repeat // Make me (one) // Copy and paste. Repeat // Make me (two) // Copy and paste. // Make me, make me Fibonacci // Make me (three) // Copy and paste. Repeat // Make me (five) // Copy and paste. Repeat // Make me (eight) // Copy and paste. // Make me, make me Fibonacci”.
El número pi es uno de los elementos matemáticos más conocidos por el público general. De hecho, el célebre día de Pi (14 de marzo, de la expresión de la fecha en inglés 3/14) ha terminado convirtiéndose en el Día Internacional de las Matemáticas desde el año 2020. Hay varias entradas en el Cuaderno de Cultura Científica sobre esta importante constante matemática, como Pi atleta, ¿Es normal el número pi? o Legislar sobre una verdad matemática.
El número Pi es la relación entre la longitud de una circunferencia y su diámetro. Es un número irracional, luego tiene infinitos decimales no periódicos y empieza así 3,141592653589793238462643383279502884197169399375105820974944…
En 2006, cuando preparaba mi colaboración semanal en el programa Graffiti de Radio Euskadi, descubrí una interesante canción sobre el número Pi. Buscaba música para poner en el programa y encontré la canción Pi, de la cantante británica Kate Bush, perteneciente al álbum Aerial (2005). Me enganchó la canción y me compré este interesante disco. La canción la podéis escuchar, por ejemplo, en YouTube.

Analicemos brevemente la sencilla letra de la misma, en la que además se recitan los primeros decimales de Pi. La canción empieza con la siguiente estrofa:
Sweet and gentle sensitive man // With an obsessive nature and deep fascination // For numbers // And a complete infatuation with the calculation // Of PI
Que podemos traducir más o menos como sigue: “Dulce y amable hombre sensible, con una naturaleza obsesiva y una profunda fascinación por los números y una completa obsesión por el cálculo de Pi”. Y continúa con el coro:
Oh he love, he love, he love // He does love his numbers // And they run, they run, they run him //In a great big circle // In a circle of infinity
Algo así como: “Oh él adora, adora, adora, él adora sus números, y ellos circulan, circulan, circulan, en un gran círculo, en un círculo de infinitud”. Y entonces empieza a cantar los decimales del número Pi:
3.1415926535 897932 // 3846 264 338 3279
Y vuelve el coro, para después continuar con los decimales de Pi:
50288419 716939937510 // 582319749 44 59230781 // 6406286208 821 4808651 32
De nuevo continua el coro y Kate Bush sigue cantando los decimales de la constante matemática:
82306647 0938446095 505 8223…
Como anécdota comentaré que mientras estaba preparando esta entrada del Cuaderno de Cultura Científica me ha dado por revisar los decimales cantados por Kate Bush en esta bonita canción y he descubierto que hay un error (canta 31 cuando debería cantar 0) y hay decimales intermedios que no canta (99 8628034825 3421170679), como se muestra a continuación.
Decimales reales del número Pi:
3,1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223…
Decimales cantados por Kate Bush del número Pi:
3.1415926535 8979323846 2643383279 5028841971 6939937510
58231974944 5923078164 06286208
8214808651 3282306647 0938446095 5058223…
Desconozco si existe algún motivo por el que Kate Bush ha cambiado esos decimales, si es que lo hay, o simplemente es un error. En cualquier caso, sigue siendo una bella canción.

El grupo estadounidense Artichoke, que mencionaba al principio de esta entrada en relación con sus dos álbumes, 26 scientists, volume one, Anning-Malthaus y 26 scientists, volume two, Newton-Zeno, también dedica una canción a la relación entre la longitud de la circunferencia y su diámetro. En su disco de 2012, titulado Etchy Sketchy Skies, incluía la canción Coffee and Pi: Daydream of a Mathematician.
Como siempre hay que escuchar la canción, lo cual lo podéis hacer aquí.
La letra de esta canción dice lo siguiente:
I guess but I don’t know and this is helpful at parties and so on // A lot of things are beautiful especially when you’re very very very close // A lot of things are beautiful especially when you’re backin’ way up // A coffee-drinkin machine (they call me) I am a fiend for that bean! // A coffee-drinkin’ machine // I see circles // With my circles // It’s funny that the pi never stops (why doesn’t) // Funny like the shape of a blur // It’s funny that the pi never stops (why doesn’t) // Pi stop pi stop? Pi stop pi stop? // I guess but I don’t know and this is helpful at parties and so on // A lot of things are circular especially when you’re vey very very close // A lot of things are circular especially when you’re backin’ way up // A coffee-drinkin’ machine (they call me) hey what’s the shape of that // bean? // A coffee-drinkin’ machine // I see cones and rodes // With my cones and rods // It’s funny that the pi never stops (why doesn’t) // Funny like the shape of a blur // It’s funny that the pi never stops (why doesn’t) // Pi stop pi stop? Pi stop pi stop? // If the pi isn’t stoppin’ for us maybe we should stop for some pie
Esta vez no traduciré toda la letra de la canción, simplemente algunos versos. Por ejemplo, cuando dice It’s funny that the pi never stops (why doesn’t) / Funny like the shape of a blur, que podríamos traducir como “Es divertido que el número Pi nunca se detenga (¿por qué no lo hace?) / Divertido como la forma de una mancha”. O el verso final If the pi isn’t stoppin’ for us maybe we should stop for some pie, que podríamos traducir “Si el número Pi no se detiene para nosotros, quizás nosotros deberíamos parar por un poco de tarta”, jugando con la igualdad fonética de “Pi” y “Pie” (tarta).

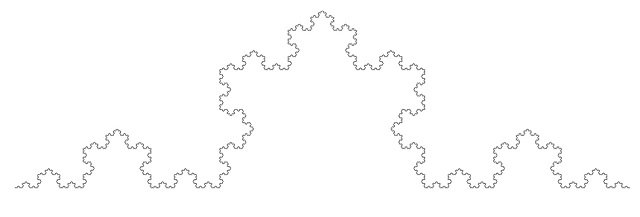
El último objeto matemático que vamos a incluir en esta entrada es el conjunto de Mandelbrot, es decir, un fractal, de hecho, el más conocido por el público general. Para una pequeña explicación del conjunto de Mandelbrot podéis leer la entrada Guía matemática para el cómic ‘Promethea’ y para una pequeña introducción a los fractales, la entrada Fractus, arte y matemáticas.
La canción que vamos a escuchar ahora es Mandelbrot set (2008), del músico y letrista norteamericano Jonathan Coulton, conocido por sus canciones sobre la “cultura geek” (de los entusiastas de los ordenadores). Su música se suele clasificar como folk rock. Esta es la canción (el video incluye hermosos zooms sobre el conjunto de Mandelbrot): Mandelbrot set.
La letra realmente es para analizarla con detenimiento ya que explica muchas cosas sobre los fractales y el conjunto de Mandelbrot, aunque en esta entrada solo comentaremos algunas estrofas. La primera dice así:
“Pathological monsters!” // Cried the terrified mathematician // Every one of them is a splinter in my eye.
Que podríamos traducir como “¡Monstruos patológicos! gritó el aterrorizado matemático, cada uno de ellos es una astilla en mi ojo”. Este párrafo hace referencia al origen de los fractales, a finales del siglo XIX y principios del XX, cuando grandes matemáticos como Riemann, Cantor, Peano, Hilbert, Sierpinski o Hausdorff, entre otros, introdujeron algunas construcciones matemáticas “patológicas”, los primeros objetos fractales, con propiedades geométricas o analíticas contrarias a la intuición matemática, por ese motivo la matemática de ese tiempo los consideró “monstruos patológicos” que no podían existir. Pero la letra de la canción sigue así:
I hate the Peano Space and the Koch Curve // I fear the Cantor Ternary Set // The Sierpinski Gasket makes me wanna cry
Que podríamos traducir “Odio el espacio de Peano y la curva de Koch, me produce terror el conjunto ternacio de Cantor y el triángulo de Sierpinski me hace llorar”. Coulton menciona diferentes fractales muy conocidos y el terror que le provocan, ya que son “monstruos matemáticos”.
La letra de la canción de Jonathan Coulton continúa así:
And a million miles away // A butterfly flapped its wings // On a cold November day // A man named Benoit Mandelbrot was born
Que nos remite a la teoría del caos y al efecto mariposa cuando en los dos primeros versos dice “Y a un millón de millas de distancia una mariposa batió sus alas”, para después mencionar al matemático considerado el “padre” de los fractales, el polaco nacionalizado francés y estadounidense Benoit Mandelbrot (1924-2010), quien realmente dio un impulso enorme a los fractales: “En un día frío de noviembre nació un hombre llamado Benoit Mandelbrot”. Las tres siguientes estrofas están relacionadas con el trabajo de este matemático.
His disdain for pure mathematics // And his unique geometrical insights // Left him well equipped to face those demons down
Algo así como que era la persona adecuada para estudiar estos singulares objetos matemáticos: “Su desdén por las matemáticas puras y sus percepciones geométricas únicas, le tenían bien equipado para enfrentarse a esos demonios”. Y continúa en los siguientes versos “Él vio que esa complejidad infinita podía ser descrita por sencillas reglas, usó su gran cerebro para darle la vuelta al juego”, más aún “Y miró debajo de la tormenta y tuvo una visión en su cabeza, una forma bulbosa puntiaguda” refiriéndose al que hoy llamamos conjunto de Mandelbrot, para terminar “Cogió su lápiz y desveló su secreto”.
He saw that infinite complexity // Could be described by simple rules // Used his giant brain to turn the game around // And he looked below the storm // And saw a vision in his head // A bulbous pointy form // Picked his pencil up and he wrote his secret down
Y continúa describiendo matemáticamente el conjunto de Mandelbrot, describiendo cuando un punto del plano complejo pertenece al conjunto de Mandelbrot, más o menos como se describe en la entrada Guía matemática para el cómic ‘Promethea’, donde comentamos:
Dado un número complejo c (por lo tanto, también nos indica un punto del plano coordenado), se toma la sucesión recursiva siguiente:
Si la sucesión se va hacia infinito, entonces el elemento del plano complejo c no pertenece al conjunto de Mandelbrot, mientras que, si se mantiene acotada, entonces c es un punto del conjunto de Mandelbrot.
La única diferencia es que Coulton parte de un número complejo cualquiera z, en lugar de 0. De hecho, la letra dice así:
Just take a point called Z in the complex plane // Let Z1 be Z squared plus C // And Z2 is Z1 squared plus C // And Z3 is Z2 squared plus C // And so on // If the series of Z’s should always stay // Close to Z and never trend away // That point is in the Mandelbrot Set
Y continúa la canción, aunque eso ya os lo dejo para vosotras, las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica.

Vamos a terminar esta entrada con un disco instrumental, Sacred Geometry (2017), de la compositora y violinista Jezabel Martínez. Este disco de música para relajarse, que en palabras de su autora “ha sido compuesto teniendo en cuenta la matemática que reside en la Geometría y la Música”, incluye temas como Sphere; Spiral; Fractal I, II, II; Aureum; Number Pi; o Fibonacci Sequence, entre otros.
Os dejo con la canción Number Pi, aunque podéis escuchar este disco en la página web de Jezabel Martínez o en los lugares habituales de música (Spotify, Youtube, etc).

Y en una siguiente entrada, que podríamos titular El teorema musical, hablaremos de canciones sobre resultados matemáticos.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Nota del editor:
[*] Estas medidas se dan en pulgadas. Si hubiese usado una cinta métrica en centímetros habría obtenido en vez de 37, 29 y 37 los valores aproximados 94, 74, 94, o 91 en el caso del 36. Los números medidos son culturales, por tanto.
qbit
PDP-1 fue uno de los primeros ordenadores, y Brainfuck es un lenguaje de programación ofuscado.
El teorema musical — Cuaderno de Cultura Científica
[…] de nuestra anterior entrada del Cuaderno de Cultura Científica, ¡Música, matemática!, que tenía como objetivo mostrar algunas canciones, de grupos con diferentes estilos musicales, […]
Inazio
Muy buenos artículos musicales. Creo que en alguno de los dos también tendría cabida esta canción de Josele Santiago: «Fractales»
https://youtu.be/1o8943Emmk4
Música matemática – ConCiencia2
[…] Fuente: Música matemática. Raúl Ibáñez , profesor del Departamento de Matemáticas de la UPV/E… […]