La conocida como identidad de Proizvolov fue propuesta por el matemático Vyacheslav Proizvolov en forma de problema en las Olimpiadas Matemáticas Soviéticas de 1985:

Consideremos el conjunto de los primeros 2N enteros positivos,

C_N = {1, 2, 3, …, 2N − 1, 2N},

y una partición de él en dos subconjuntos de N elementos cada uno de ellos:

A_N = {a₁, a₂, …, a_N-1, a_N} y B_N = {b₁, b₂, …, b_N-1, b_N}.

Ordenemos los elementos de ambos conjuntos de la siguiente manera:

Se pide probar que la siguiente suma de valores absolutos

|a₁ – b₁| + |a₂ – b₂| + … + |a_N-1 – b_N-1| + |a_N – b_N|

es igual a N².

Un ejemplo

Para entender mejor el enunciado, vamos a ver un ejemplo. Si N = 10, tenemos el conjunto de los veinte primeros números naturales

C₁₀ = {1, 2, 3, …, 19, 20}.

Elegimos las particiones (hemos ordenado los números de la primera partición de manera creciente y los de la segunda de manera decreciente):

A₁₀ = {1, 3, 4, 7, 8, 9, 10, 18, 19, 20}, y

B₁₀ = {17, 16, 15, 14, 13, 12, 11, 6, 5, 2},

Es decir, a₁ = 1, a₂ = 3, a₃ = 4, …, a₉ = 19, a₁₀ = 20, b₁ = 17, b₂ = 16, b₃ = 15, …, b₉ = 5 y b₁₀ = 2.

Entonces,

|a₁ – b₁| + |a₂ – b₂| + … + |a₉ – b₉| + |a₁₀ – b₁₀| =

|1 – 17| + |3 – 16| + |4 – 15| + |7 – 14| + |8 – 13| + |9 – 12| + |10 – 11| + |18 – 6| + |19 – 5| + |20 – 2| =

16 + 13 + 11 + 7 + 5 + 3 + 1 + 12 + 14 + 18 = 100 = 10².

Una demostración sencilla de la identidad de Proizvolov

Observemos en primer lugar que |a – b| = máx{a,b} – mín{a,b}. En efecto, si a > b, es |a – b| = a – b = máx{a, b} – mín{a, b}, y si b > a, es |a – b| = b – a = máx{a, b} – mín{a, b}.

En segundo lugar, para cada i en {1, 2…, N − 1, N}, se verifica que uno de los números del par {a_i, b_i} está en el conjunto A = {1, 2…, N − 1, N} y el otro en el conjunto B = {N + 1, N + 2, …, 2N − 1, 2N}.

En efecto, si esta propiedad no fuera cierta, supongamos, por ejemplo, que los números a_i y b_i pertenecen ambos al conjunto A. Es decir, N + 1 > a_i y N + 1 > b_i. Eso significa que al menos hay i elementos del conjunto A_N que pertenecen a A (ya que N + 1 > a_i > … > a₂ > a₁) y podría haber algún otro elemento de A_N también en A) y al menos N − i + 1 elementos del conjunto B_N que pertenecen a A (ya que N + 1> b_i > b_i+1 > … > b_N-1 > b_N y podría haber algún otro elemento de B_N también en A). Es decir, en el conjunto A habría al menos i + (N – i + 1) = N + 1 elementos de C_N. Pero eso es imposible, porque A solo posee N elementos. Un argumento similar prueba que tampoco puede suceder que a_i y b_i pertenezcan ambos al conjunto B.

Es decir, efectivamente, para cada i en {1, 2…, N − 1, N}, se verifica que uno de los números del par {a_i, b_i} está en el conjunto A = {1, 2…, N − 1, N} y el otro en el conjunto B = {N + 1, N + 2, …, 2N − 1, 2N}. De aquí se deduce que para cada i en {1, 2…, N − 1, N}, es N + 1 > mín{a_i, b_i} < y máx{a_i, b_i} > N. Es decir, de otra manera,

A = {1, 2…, N − 1, N} = {mín{a_i, b_i}: i en {1, 2…, N − 1, N}}, y

B = {N + 1, N + 2, …, 2N − 1, 2N} = {máx{a_i, b_i}: i en {1, 2…, N − 1, N}}.

Por lo tanto,

|a₁ – b₁| + |a₂ – b₂| + … + |a_N-1 – b_N-1| + |a_N – b_N| =

(máx{a₁, b₁} – mín{a₁, b₁}) + (máx{a₂, b₂} – mín{a₂, b₂}) + … + (máx{a_N-1, b_N-1} – mín{a_N-1, b_N-1}) + (máx{a_N, b_N} – mín{a_N, b_N}) =

(máx{a₁, b₁} + máx{a₂, b₂} + … + máx{a_N-1, b_N-1} + máx{a_N, b_N}) – (mín{a₁, b₁} + mín {a₂, b₂} + … + mín{a_N-1, b_N-1} + mín{a_N, b_N}) =

((N + 1) + (N + 2) + … + (2N – 1) + 2N) – (1 + 2 + … + (N – 1) + N) =

((N + 1) – 1) + ((N + 2) – 2) + … + ((2N – 1) – (N – 1)) + (2N – N) =

N + N + … + N = N². QED

Una generalización de la identidad de Proizvolov

Grégoire Nicollier propuso en 2015 la siguiente generalización de la identidad de Proizvolov:

Consideremos un conjunto de números reales,

C_N = {c₁, c₂, …, c_2N-1, c_N},

y una partición de él en dos subconjuntos de N elementos cada uno de ellos:

A_N = {a₁, a₂, …, a_N-1, a_N} y B_N = {b₁, b₂, …, b_N-1, b_N}.

Ordenemos los elementos de estos conjuntos de la siguiente manera:

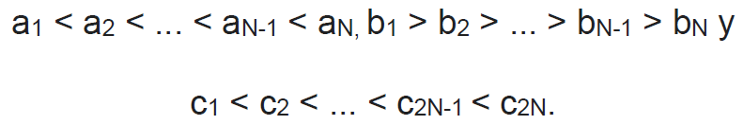
Entonces, la suma

|a₁ – b₁| + |a₂ – b₂| + … + |a_N-1 – b_N-1| + |a_N – b_N|

es independiente de las particiones elegidas A_N y B_N.

Para probar esta propiedad, basta con observar, con un argumento similar al realizado antes, que para cualquier par {a_i, b_i}, uno de los elementos es menor que c_N + 1 y el otro es mayor que c_N. Entonces,

{c₁, c₂, …, c_N-1, c_N} = {mín{a_i, b_i}: i en {1, 2…, N − 1, N}}, y

{c_N+1, c_N+2, …, c_2N-1, c_2N} = {máx{a_i, b_i}: i en {1, 2…, N − 1, N}}.

Y por lo tanto:

|a₁ – b₁| + |a₂ – b₂| + … + |a_N-1 – b_N-1| + |a_N – b_N| =

(máx{a₁, b₁} – mín{a₁, b₁}) + (máx{a₂, b₂} – mín{a₂, b₂}) + … + (máx{a_N-1, b_N-1} – mín{a_N-1, b_N-1}) + (máx{a_N, b_N} – mín{a_N, b_N}) =

(máx{a₁, b₁} + máx{a₂, b₂} + … + máx{a_N-1, b_N-1} + máx{a_N, b_N}) – (mín{a₁, b₁} + mín {a₂, b₂} + … + mín{a_N-1, b_N-1} + mín{a_N, b_N}) =

(c_2N + c_2N-1 + … + c_N+2 + c_N+1) – (c₁ + c₂ + … + c_N-1 + c_N),

que es la misma cantidad para cualquier partición elegida. QED

Además, Grégoire comentaba en el artículo que esta propiedad sigue siendo cierta aunque los números del conjunto C no sean todos diferentes.

¡Curiosas propiedades!

Referencias

• Proizvolov’s Identity, Futility Closet, 21 agosto 2014

• Proizvolov’s Identity, Cut the Knot

• Grégoire Nicollier, A generalisation of Proizvolov’s identity, The Mathematical Gazette 99 (546) (2015): 525-526

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad