En la anterior entrada del Cuaderno de Cultura Científica, titulada Universo pandigital, estuvimos hablando de números pandigitales, tanto de sus curiosas propiedades, como de algunos números pandigitales sorprendentes, así como de expresiones aritméticas pandigitales que se han utilizado para crear rompecabezas matemáticos, como las sumas o productos pandigitales. En esta entrada vamos a seguir en esta línea con las denominadas fracciones pandigitales, de las que ya hablamos de pasada en la entrada Fracciones sorprendentes.

El primer problema de ingenio publicado que esté relacionado con las fracciones pandigitales está recogido, según el matemático estadounidense David Singmaster, en el libro Mathematische Kurzweil (Diversión matemática) del alemán Louis Mittenzwey, publicado en Leipzig en 1880.

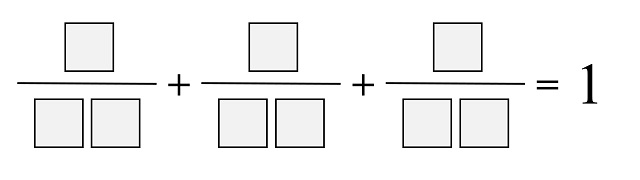
Problema 141 (Louis Mittenzwey): Utilizar las cifras 1, 2, …, 9 para formar tres fracciones cuya suma sea uno (1).

Las soluciones que aparecen en el texto son:

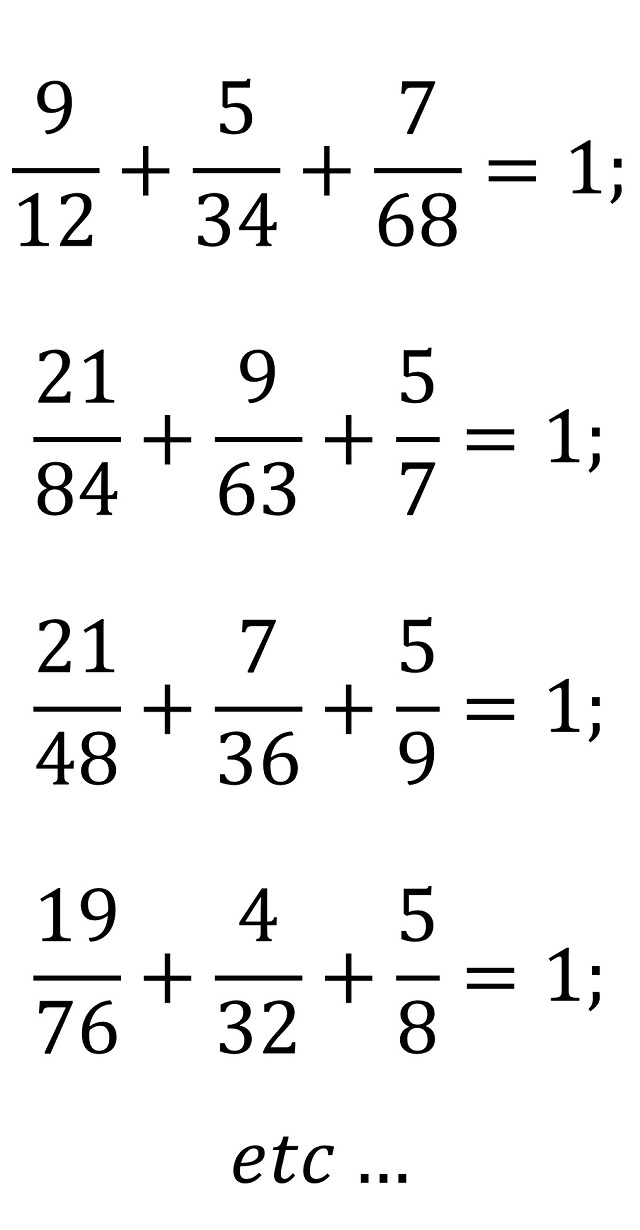
El inventor, coleccionista y comunicador de rompecabezas matemáticos y juegos de ingenio japonés Nob Yoshigahara (1936-2004), quien recibió el Premio Sam Loyd en 2003, recuperó este problema, pero solo para fracciones de la forma a/bc, de manera que es problema se podría plantear de la siguiente forma.

Problema (Nob Yoshigahara): Colocar las cifras 1, 2, 3, …, 9 en las casillas para que la siguiente suma de fracciones tenga sentido.

La única solución es la de este tipo que aparece como solución al problema 141, de Louis Mittenzwey.

Con motivo de mi entrada Universo pandigital, José Hernández (de Apuntes Misceláneos) me comentaba en Facebook que el matemático colombiano Bernardo Recamán Santos (imagino que en su libro Las nueve cifras y el cambiante cero, publicado por la editorial Gedisa) incluía una versión más extendida de este, ya que permitía que la suma fuese no solo 1, sino cualquier número natural N.

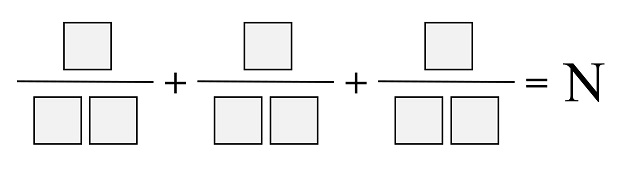
Para las personas que estáis leyendo esto queda este problema, para los casos en los que N no es 1. ¡A divertirse!

La siguiente aparición de fracciones pandigitales en libros de rompecabezas matemáticos fue en el texto Libro de puzzles estándar del siglo XX (1907), de Arthur Cyril Pearson. Curiosamente no aparecen como un problema abierto, sino como una anécdota numérica, titulada Malabares con las cifras.

Malabares con las cifras: Las nueve cifras básicas 1, 2, 3, …, 9 pueden ser colocadas de forma que se obtengan fracciones equivalentes a una de las siguientes 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8 y 1/9, como

Por supuesto, que hay más formas de conseguirlo. De hecho, David Wells en su libro The Penguin Dictionary of Curious and Interesting Numbers comenta que existen existen 12 formas curiosas de utilizar las 9 cifras básicas, 1, 2, 3, 4, 5, 6, 7, 8, 9, para escribir la fracción 1/2. Las formas, más pequeña y mayor, son: 6729/13458 y 9327/18654.

Como no podía ser de otra forma, volvemos a encontrarnos al inventor de rompecabezas matemáticos y juegos de ingenio británico Henry E. Dudeney (1857-1930). En su celebrado libro Amusements in Mathematics / Diversiones matemáticas (1917) aparecen varios problemas, como el problema 88, llamado división digital.

División digital (Henry E. Dudeney): Otro buen rompecabezas consiste en ordenar las nueve cifras (excluyendo el cero) en dos grupos, de modo que uno de ellos, al ser dividido por el otro, produzca un número determinado sin resto. Por ejemplo, 13.458 dividido por 6.729 da 2. ¿Puede el lector encontrar distribuciones similares que produzcan 3, 4, 5, 6, 7, 8 y 9 respectivamente? Además, ¿puede encontrar los pares de números más pequeños posibles en cada caso? Así, 14.658 dividido por 7.329 es tan correcto para 2 como el anterior ejemplo que hemos dado, pero los números son mayores.

Antes de adentrarnos en la solución a este problema (que obviamente está ligado al anterior), comentar que existen algunas curiosidades más relacionadas con este problema. Por ejemplo, si tomamos la fracción 14.865/2.973, que es igual a 5, resulta que reordenando los dígitos de numerador y denominador obtenemos de nuevo una fracción pandigital cuyo valor es también 5, en concreto, 18.645/3.729. Aunque ninguna de ellas es la buscada, la fracción de números más pequeños posibles. Esta es 13.485/2.697, que también podemos reordenar para obtener una cuarta fracción pandigital de valor 5, 13.845/2.769.

La solución al rompecabezas de la división digital es la siguiente:

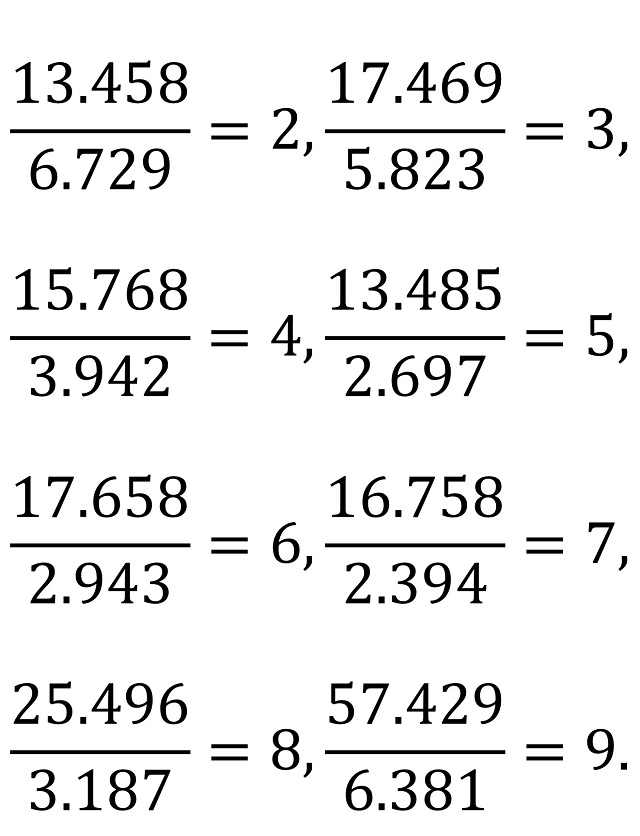
A este problema le seguían otros en el libro, como el problema 90, llamado el rompecabezas del siglo.

El rompecabezas del siglo: ¿Puede el lector escribir 100 en forma de un número mixto, utilizando cada una de las nueve cifras, una vez y sólo una vez? El distinguido matemático francés Edouard Lucas, ya fallecido, encontró siete formas diferentes de hacerlo, y expresó sus dudas sobre la existencia de otras formas. De hecho, sólo hay once formas y ninguna más. Aquí está una de ellas, 91 5.742/638. Nueve de las otras formas tienen igualmente dos cifras en la parte integral del número, pero la undécima expresión sólo tiene una cifra. ¿Puede el lector encontrar esta última forma?

Antes de continuar, recordemos a qué se refiere el autor con un número mixto y por qué el número 91 5.742/638 lo es. Para empezar, en la entrada Números errores de impresión), estuvimos hablando de lo que se conoce como fracciones mixtas. Una fracción mixta es una fracción impropia, es decir, el numerador es mayor que el denominador (ambos positivos), luego su valor es mayor que 1, que se representa como un número entero y una fracción propia. Por ejemplo, 3/2 es una fracción impropia, que se representa como 3/2 = 1 1/2, queriendo indicar que es la suma de 1 y 1/2 (esto es, 3/2 = 1 + 1/2, pero en la representación de la fracción mixta se omite el +). Cuando Dudeney habla de un número mixto sería una expresión de ese tipo, pero tal que la parte de la fracción no es una fracción propia, sino que su valor es un número natural. Así, el número mixto que aparece en el enunciado del rompecabezas es 91 5.742/638, cuyo valor es 91 + 5.742/638 = 91 + 9 = 100.

La solución a este problema la podéis intentar buscar vosotros mismos, ya que es la diversión que esconden los rompecabezas matemáticos. En cualquier caso, para quienes quieran consultarla o comprobar si la han obtenido, aquí la tenéis.

Pero Dudeney plantea, en el problema 91 (llamado Más números mixtos), también obtener números mixtos pandigitales cuyo valor sea cualquier número menor que 100.

Más números mixtos: Cuando publiqué por primera vez mi solución al último acertijo, me vi obligado a intentar la expresión de todos los números sucesivos hasta el 100 mediante una fracción mixta que contuviera las nueve cifras. Aquí hay doce números para que el lector pruebe su mano: 13, 14, 15, 16, 18, 20, 27, 36, 40, 69, 72, 94. Utilice cada una de las nueve cifras una vez, y sólo una vez, en cada caso.

Dudeney da las soluciones para esos números que plantea, por ejemplo, para 13 sería el número mixto 9 5.472/1368 = 13, aunque también puede haber soluciones para otros números menores que 100. Dejamos este rompecabezas sin resolver para las personas que estáis leyendo esta entrada.

Por otra parte, el gran matemático italiano Giuseppe Peano (1858-1932), a quienes muchos relacionan con la curva de Peano o los axiomas de Peano, entre muchas otras aportaciones matemáticas, publicó en 1925 el libro Giochi di aritmetica e problemi interessanti / Juegos aritméticos y problemas interesantes, que contenía la siguiente cuestión interesante relacionada con las expresiones aritméticas pandigitales. Daba las seis formas de expresar 9 como ABCDE/FGHIJ, utilizando las 10 cifras básicas, del 0 al 9 (en tres de ellas F = 0).

Y con estas curiosas fracciones pandigitales concluimos esta entrada del Cuaderno de Cultura Científica.

Bibliografía:

1.- Raúl Ibáñez, La gran familia de los números, Catarata, 2021.

2.- David Singmaster, Sources in recreational mathematics, an annotated bibliography

3.- A. Cyril Pearson, Twentieth Century Standard Puzzle Book (Libro de puzzles estándar del siglo XX), George Routledge & Sons, 1907.

Versión digital en la Librería Gutenberg: The Project Gutenberg EBook of Twentieth Century Standard Puzzle Book, by Cyril Pearson.

5.- Henry E. Dudeney, Amusements in Mathematics, Thomas Nelson and sons,1917 (el original puede verse en la librería Internet Archive).

6.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.

7.- Giuseppe Peano, Giochi di aritmetica e problemi interessanti, Paravia, 1925 (el original puede verse en la librería Internet Archive ).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica