Hace unos días estaba yo documentándome sobre ejemplos de arte textil relacionados con los cuadrados latinos cuando me encontré con el trabajo del biólogo, estadístico, coleccionista de arte textil y artista textil estadounidense Stephen Threlkeld. En la galería de arte Oxford Treehouse Gallery (Oxford Mississippi, Estados Unidos) me encontré con dos obras textiles que llamaron mi atención, Fibonacci Spiral (espiral de Fibonacci) y Latin Square I (cuadrado latino I).

La primera pieza textil, Fibonacci Spiral (espiral de Fibonacci), está relacionada con la famosa sucesión de Fibonacci (véanse las entradas ¡Póngame media docena de fibonaccis!, El origen poético de los números de Fibonacci o Poemas Fibonacci). Esta sucesión numérica empieza con los siguientes números 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, etcétera, y tiene la propiedad de que cada término de la sucesión es la suma de los dos términos anteriores. A partir de esta sucesión se puede construir una espiral de la siguiente forma. Primero se construye una sucesión de cuadrados, cuyos lados están determinados por los números de la sucesión, que se unen formando un rectángulo de la siguiente forma.

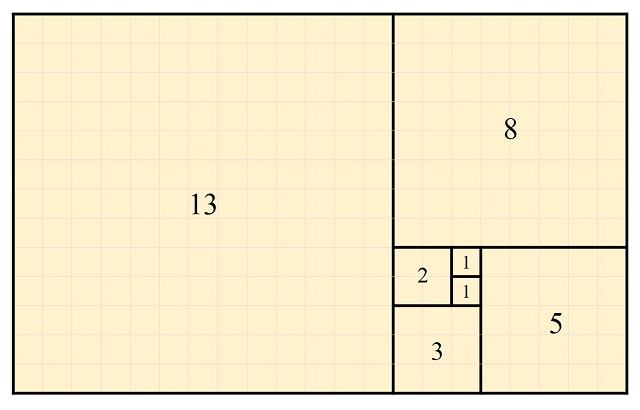
Después, en cada cuadrado se traza un arco de circunferencia, de radio igual al lado del correspondiente cuadrado, de forma que la unión de los arcos forma una espiral (véase la siguiente imagen) que recibe el nombre de espiral de Fibonacci.

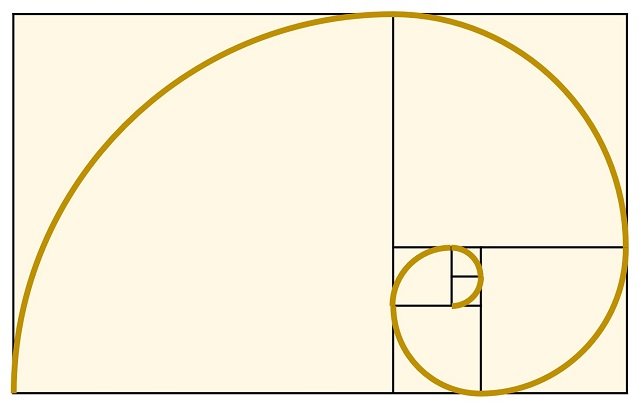
La segunda obra textil, Latin Square I (cuadrado latino I), es la que llamó mi atención desde la perspectiva de encontrar arte textil relacionado con los cuadrados latinos. Esta obra es, de hecho, un cuadrado latino de orden 5 formado por colores. Recordemos que un cuadrado latino de orden n es un retículo cuadrado de tamaño n x n en el que cada entrada es un número del 1 al n (aunque bien pueden considerarse n símbolos cualesquiera, por ejemplo, las letras del alfabeto latino que utilizó el matemático suizo Leonhard Euler o los colores utilizados por algunos artistas contemporáneos, como el artista concreto Richard P. Lohse o el artista textil Stephen Threlkeld, una de cuyas obras se muestra en la siguiente imagen), de tal forma que cada número de {1,…, n} aparece una vez, y sólo una vez, en cada fila y cada columna. Para más información sobre los cuadrados latinos véase la entrada Cuadrados latinos, matemáticas y arte abstracto.

Si asignamos los números 1, 2, 3, 4, 5 a los colores de la primera fila, el cuadrado latino de orden 5 numérico, asociado al anterior cuadrado latino de colores, es el que aparece en la siguiente imagen.

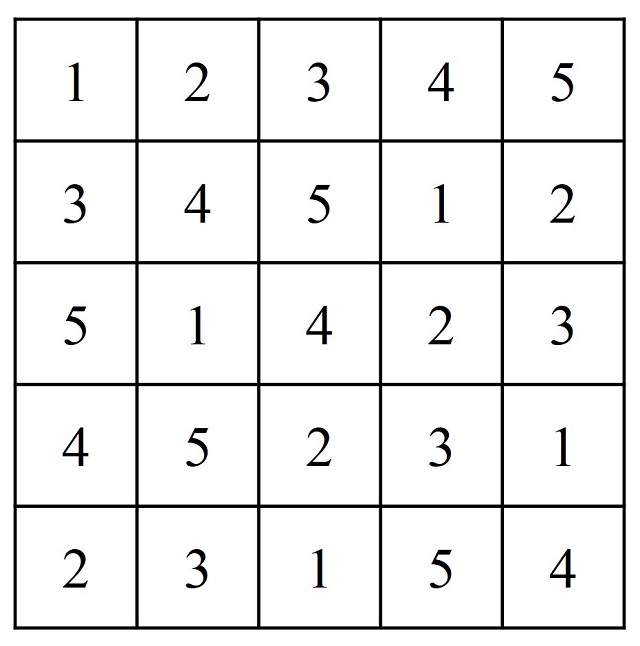
Tanto este cuadrado latino, como el que aparece en otra de sus obras, Latin Square II (cuadrado latino II), son cuadrados latinos de orden 5 que no están ligados a un grupo algebraico, es decir, no son la tabla de Cayley de un grupo finito de 5 elementos (para más información sobre la relación entre cuadrados latinos y grupos algebraicos, véase la entrada Cuadrados latinos, matemáticas y arte abstracto o el libro Cayley, el origen del algebra moderna). Esta era una propiedad que a mí me interesaba especialmente, aunque el interés de Stephen Threlkeld en los cuadrados latinos, como entenderemos en un momento, no estaba relacionado con el álgebra moderna, sino con su utilización en el diseño de experimentos estadísticos (también en la entrada Cuadrados latinos, matemáticas y arte abstracto se muestra un sencillo ejemplo de este tipo de aplicación en estadística).

Para entender el interés de Stephen Threlkeld en los cuadrados latinos hay que saber más sobre este artista. En la página de la galería de arte Oxford Treehouse Gallery dan una pequeña reseña biográfica que nos permitirá conocerle un poco mejor y entender el motivo de su interés en estos objetos combinatorios.

Stephen Threlkeld se licenció en Oceanografía y se doctoró en Zoología, trabajó como ecólogo acuático y estadístico, fue autor y editor durante unos 40 años, así como profesor de biología. En paralelo, llevaba una segunda vida como coleccionista de arte.

Tras sus primeras incursiones en la pintura y el diseño gráfico, tomó clases para aprender a tejer en Nuevo México y Carolina del Norte, y ahora se expresa artísticamente a través de este medio. Sus tejidos se inspiran a menudo en rasgos y colores del paisaje americano, y a veces incluyen series matemáticas o temas biológicos.

Aunque en esta pequeña reseña biográfica ya nos dan una pista de cuál podía ser el interés de Threlkeld por los cuadrados latinos, cuando me puse en contacto con él, por correo electrónico, para interesarme por estas obras me confirmó que durante sus años de profesor de biología había enseñado en sus clases diseño de experimentos estadísticos.

Por otra parte, en nuestra comunicación por correo electrónico, Stephen Threlkeld llamó mi atención sobre una obra textil suya que yo no había descubierto en mi búsqueda, The Welsh Lawyer (el abogado galés), que estaba basada en el “rompecabezas/problema del abogado galés”, que el estadístico y biólogo británico Ronald A. Fisher (1890-1962), autor del libro The Designs of Experiments / El diseño de experimentos (1935), había propuesto en su libro.

Efectivamente, el estadístico y biólogo Ronald Fisher incluye el siguiente rompecabezas en su libro El diseño de experimentos, por el siguiente motivo, “es útil para familiarizar la mente con las relaciones combinatorias que subyacen en el uso del cuadrado latino, y similares, para el diseño experimental”.

Rompecabezas del abogado galés: Dieciséis pasajeros de un transatlántico descubren que son un grupo excepcionalmente representativo. Cuatro son ingleses, cuatro escoceses, cuatro irlandeses y cuatro galeses. También hay cuatro de cuatro edades diferentes, 35, 45, 55 y 65 años, y no hay dos de la misma edad que sean de la misma nacionalidad. Por profesión, cuatro son abogados, cuatro soldados, cuatro médicos y cuatro clérigos, y no hay dos de la misma profesión con la misma edad o nacionalidad.

También resulta que cuatro son solteros, cuatro casados, cuatro viudos y cuatro divorciados, y que no hay dos del mismo estado civil que tengan la misma profesión, ni la misma edad, ni la misma nacionalidad. Por último, cuatro son conservadores, cuatro liberales, cuatro socialistas y cuatro fascistas, y no hay dos de las mismas simpatías políticas que tengan el mismo estado civil, ni la misma profesión, ni la misma edad, ni la misma nacionalidad.

Se sabe que tres de los fascistas son un abogado inglés soltero de 65 años, un militar escocés casado de 55 años y un médico irlandés viudo de 45 años. Es fácil entonces precisar el fascista restante.

Además, el socialista irlandés tiene 35 años, el conservador de 45 años es escocés y el inglés de 55 años es clérigo. ¿Qué sabes del abogado galés?

La solución de este rompecabezas está relacionada, como mencionaba R. A. Fisher, con los cuadrados latinos, más concretamente con los cuadrados latinos mutuamente ortogonales. A continuación, expliquemos brevemente qué son estos objetos combinatorios, de los que ya habíamos hablado en la entrada Los cuadrados greco-latinos de Leonhard Euler.

Para introducir los cuadrados latinos mutuamente ortogonales vamos a aprovechar un rompecabezas clásico, relacionado con este concepto. En 1725, el matemático francés Jacques Ozanam (1640-1718) incluye en su libro Récréations mathématiques et physiques el siguiente rompecabezas con cartas.

Rompecabezas con cartas de Jacques Ozanam: Colocar los reyes, reinas, jotas y ases de una baraja de cartas, formando un cuadrado 4 x 4, tal que cada fila y cada columna contenga una vez, y solo una vez, cada una de las figuras y cada uno de los palos.

Si nos fijamos un momento en el rompecabezas podemos descubrir que en las soluciones al mismo, ya que hay más de una solución, hay dos cuadrados latinos implicados. Si nos fijamos solo en las figuras (reyes, reinas, jotas y ases) estas forman un cuadrado latino, ya que en la solución “cada fila y cada columna contiene una vez, y solo una vez, cada una de las figuras”, lo mismo ocurre si solo nos fijamos en los palos (corazones, diamantes, tréboles y picas, en la baraja francesa, o copas, oros, bastos y espadas, en la baraja española). Por otra parte, estos dos cuadrados latinos están relacionados por el hecho de que cada carta tiene una figura y un palo, y esa carta es la única con esa figura y ese palo. Esta propiedad es la que nos va a indicar que los dos cuadrados latinos, de figuras y de palos, son mutuamente ortogonales. Pero antes de meternos en este concepto combinatorio, veamos alguna solución del rompecabezas de las cartas de Jacques Ozanam.

Como vemos en la imagen, tanto las figuras, como los palos, de estas dos soluciones, son cuadrados latinos. Pero vayamos al concepto matemático que recoge que los cuadrados latinos sean mutuamente ortogonales.

Dados dos cuadrados latinos L₁ y L₂ de orden n (es decir, que son retículas de tamaño n x n con una serie de n símbolos, por ejemplo, los números del 1 al n, distribuidos en la retícula según el concepto de cuadrado latino, luego cada símbolo aparece una vez, y sólo una vez, en cada fila y cada columna) se puede construir con ellos un nuevo retículo cuadrado n x n formado por pares ordenados de símbolos de esos dos cuadrados latinos, de forma que cada casilla del retículo está formada por el par ordenado que consiste en el símbolo de la misma casilla del cuadrado latino L₁ y el símbolo de la misma casilla de L₂ (los símbolos de cada cuadrado latino pueden ser distintos, por ejemplo, Leonhard Euler utilizaba letras latinas para uno de los cuadrados latinos y letras griegas para otro, por eso, al retículo que se forma con los dos se le suele llamar cuadrado greco-latino). Entonces, se dice que los cuadrados latinos son mutuamente ortogonales si cada uno de los n² posibles pares ordenados, formados por los n símbolos, aparece exactamente una vez en toda la retícula n x n, como en el siguiente ejemplo.

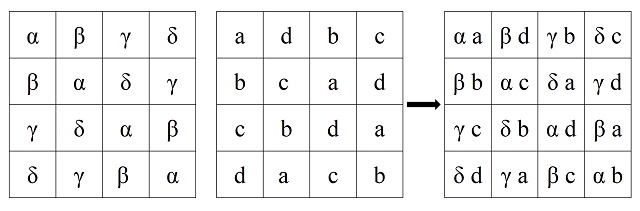
Como se observa en la anterior imagen tenemos dos cuadrados latinos de orden 4, uno con letras griegas y otro con letras latinas, de forma que al formar el retículo 4 x 4 de los pares ordenados están las 16 combinaciones posibles de pares de letra griega y letras latina (y solo una vez). Aunque si preferís ver el ejemplo con números, sería el que aparece en la siguiente imagen.

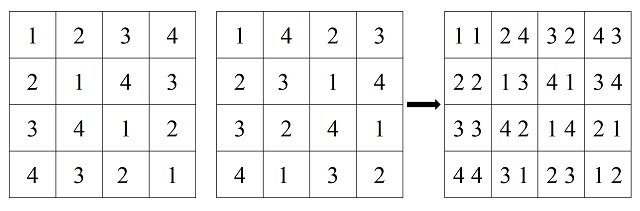
Hemos visto dos cuadrados latinos de orden 4 que son mutuamente ortogonales, pero también existen cuadrados latinos (como el siguiente, de orden 4) que no admiten ningún cuadrado latino tal que ambos sean mutuamente ortogonales.

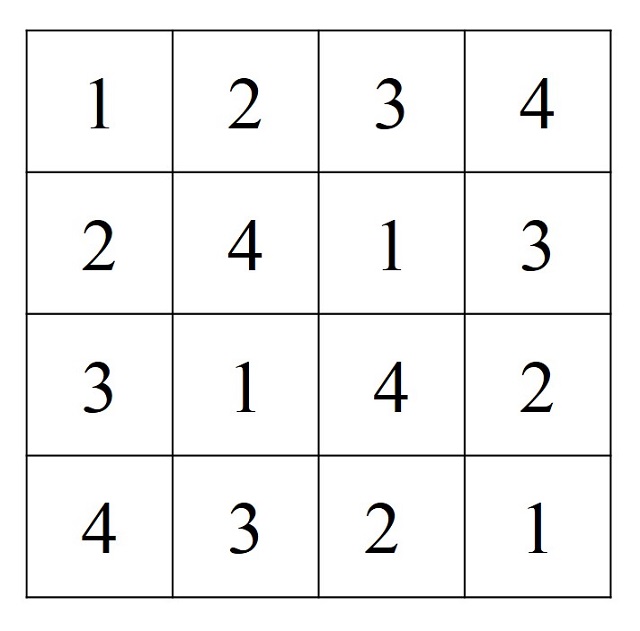
No es difícil demostrar que no existe un cuadrado latino de orden 4 que junto al anterior sean mutuamente ortogonales. Dejo esta pequeña cuestión como problema para quien quiera disfrutar del placer de la demostración.

Como se explica en la entrada Los cuadrados greco-latinos de Leonhard Euler, el matemático suizo Leonhard Euler introdujo y estudió, en los artículos De Quadratis Magicis (1776) y Recherches sur une nouvelle espece de carrés magiques (1782), los cuadrados greco-latinos como un nuevo método para construir cuadrados mágicos, aunque también el matemático coreano Choi Seok-jeong (1646-1715), en su texto Gusuryak (1700), utilizó cuadrados latinos ortogonales para construir un cuadrado mágico (véase Las matemáticas como herramienta de creación artística).

Por otra parte, el concepto de cuadrados latinos mutuamente ortogonales se puede extender a más de dos cuadrados latinos de la siguiente forma. Dados k cuadrados latinos de orden n, L₁, L₂, …, L_k, se dice que son mutuamente ortogonales si son mutuamente ortogonales dos a dos. Veamos un par de ejemplos. El primero está formado por los siguientes tres cuadrados latinos mutuamente ortogonales.

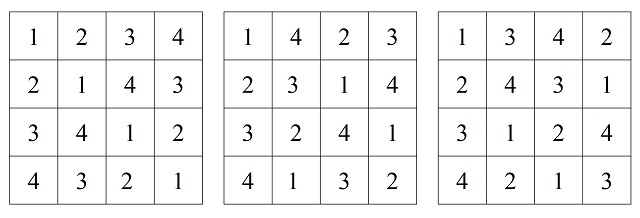
Los dos primeros claramente son mutuamente ortogonales ya que son el ejemplo que hemos mostrado más arriba. Además, el primero y el tercero son mutuamente ortogonales, así como el segundo y el tercero, como se puede observar a través de los retículos 4 x 4 formados a partir de esas parejas de cuadrados latinos (primero y tercero; segundo y tercero), los cuadrados greco-latinos asociados, que se muestran en la siguiente imagen.

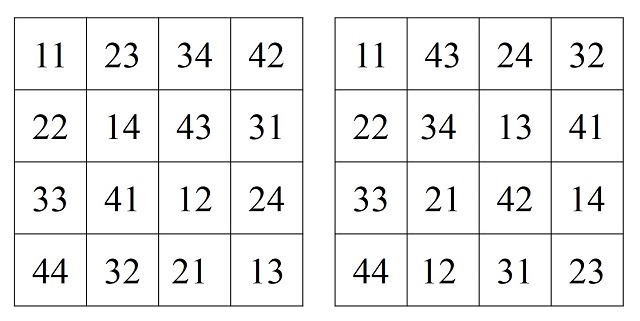
Otro ejemplo serían los siguientes cuatro cuadrados latinos de orden 5 que son también mutuamente ortogonales (como podéis comprobar vosotros mismos).

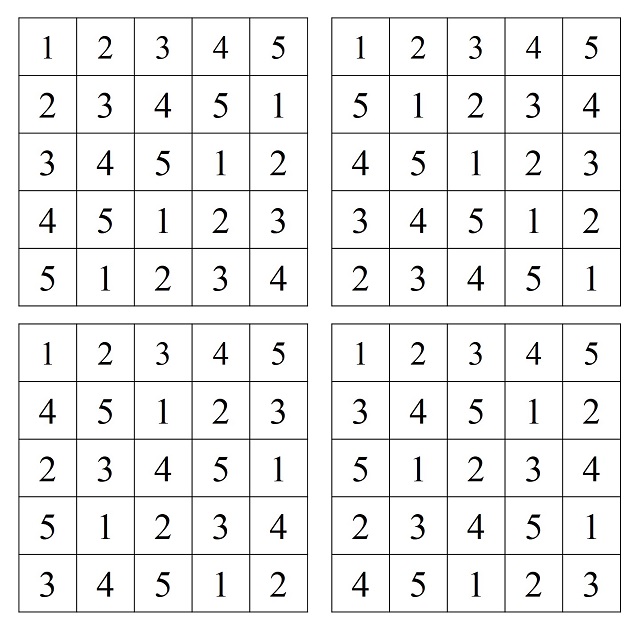
Al igual que a partir de dos cuadrados latinos de orden n mutuamente ortogonales se puede construir el nuevo retículo n x n, el cuadrado greco-latino, para k cuadrados latinos de orden n mutuamente ortogonales se puede también definir un nuevo retículo formado por las k-tuplas ordenadas de los elementos de los k cuadrados latinos, una especie de cuadrado greco-latino generalizado, que recoge la información de los k cuadrados latinos. Por ejemplo, en el caso de los tres cuadrados latinos de orden 4 mutuamente ortogonales anteriores, el cuadrado greco-latino generalizado asociado es el que aparece en la siguiente imagen.

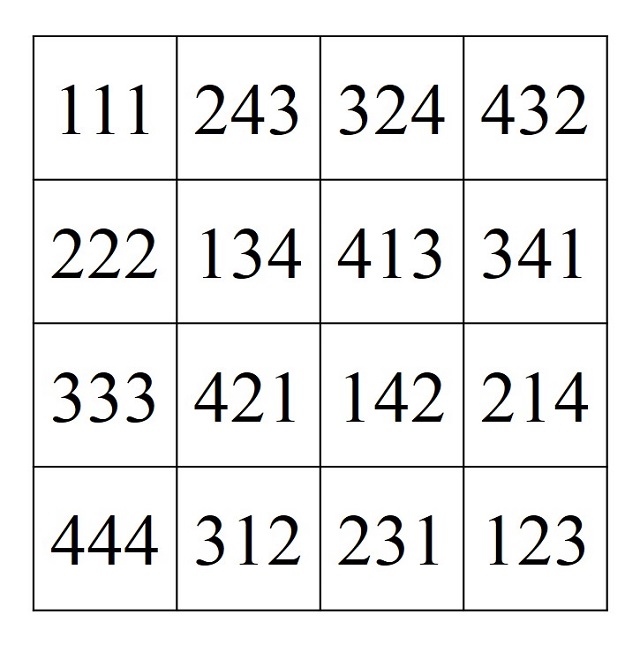
Existe mucha investigación sobre los cuadrados latinos mutuamente ortogonales, aunque en esta entrada solo vamos a comentar un resultado importante. Una pregunta lógica cuando se introduce el concepto de cuadrados latinos de orden n mutuamente ortogonales es cuántos cuadrados latinos pueden ser mutuamente ortogonales para cada orden. Por ejemplo, para orden 2 no hay cuadrados mutuamente ortogonales, ya que los dos únicos cuadrados latinos de orden 2 (véase la siguiente imagen) no son mutuamente ortogonales.

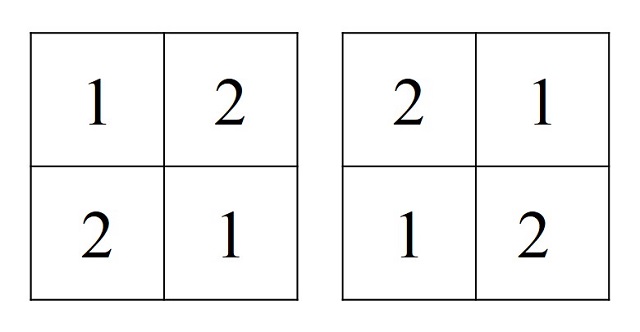
Para orden 3 solo puede haber dos cuadrados latinos que sean mutuamente ortogonales, como los de la siguiente imagen, pero no podemos conseguir tres cuadrados latinos de orden 3, entre los 12 que existen, que sean mutuamente ortogonales.

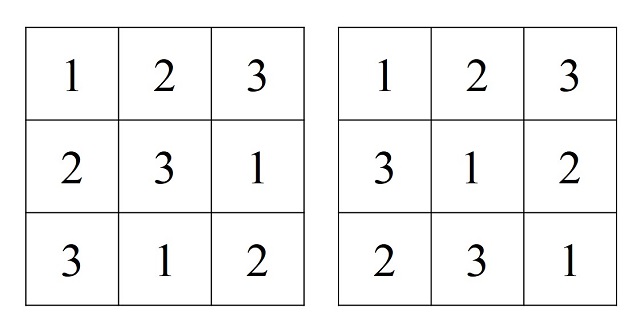
Para orden 4 solo pueden conseguirse hasta tres cuadrados latinos mutuamente ortogonales, como en el ejemplo anterior, pero ya no es posible encontrar cuatro cuadrados latinos de orden 4 que sean mutuamente ortogonales. De hecho, en general, para cuadrados latinos de orden n, la cantidad de cuadrados latinos que pueden llegar a ser mutuamente ortogonales –que se suele denotar N(n)– siempre es menor o igual que n – 1. Aunque no siempre se alcanza la cantidad n – 1. De hecho, para n = 6 no existen cuadrados latinos (de orden 6) mutuamente ortogonales, luego N(6) = 1, es la conocida conjetura de Euler, probada por el matemático amateur francés Gaston Tarry en 1901 (véase la entrada Los cuadrados greco-latinos de Leonhard Euler).

Pero volvamos al rompecabezas del abogado galés. Los datos de este problema eran los siguientes:

“Dieciséis pasajeros de un transatlántico descubren que son un grupo excepcionalmente representativo. Cuatro son ingleses, cuatro escoceses, cuatro irlandeses y cuatro galeses. También hay cuatro de cuatro edades diferentes, 35, 45, 55 y 65 años, y no hay dos de la misma edad que sean de la misma nacionalidad. Por profesión, cuatro son abogados, cuatro soldados, cuatro médicos y cuatro clérigos, y no hay dos de la misma profesión con la misma edad o nacionalidad.

También resulta que cuatro son solteros, cuatro casados, cuatro viudos y cuatro divorciados, y que no hay dos del mismo estado civil que tengan la misma profesión, ni la misma edad, ni la misma nacionalidad. Por último, cuatro son conservadores, cuatro liberales, cuatro socialistas y cuatro fascistas, y no hay dos de las mismas simpatías políticas que tengan el mismo estado civil, ni la misma profesión, ni la misma edad, ni la misma nacionalidad.”

Las hipótesis del rompecabezas nos recuerdan al concepto de cuadrados latinos mutuamente ortogonales. De hecho, se puede resolver con los tres cuadrados latinos de orden 4 anteriores (que en esencia es el único ejemplo para ese orden), como veremos a continuación.

Vamos a considerar que las columnas del cuadrado greco-latino generalizado (de orden 4) que vamos a asociar al problema, que numeramos 1, 2, 3, 4, son las nacionalidades de los pasajeros (1 = inglés, 2 = escocés, 3 = irlandés, 4 = galés) y que las filas son los estados civiles de los pasajeros (1 = divorciado, 2 = viudo, 3 = casado, 4 = soltero). Además, vamos a designar con las cuatro primeras letras griegas (alpha, beta, gamma, delta) las simpatías políticas, que representaremos como el primer cuadrado latino del ejemplo anterior (ya que sabemos que ninguno de los pasajeros comparte nacionalidad, estado civil y simpatías políticas, aunque aún no sabemos la correspondencia con las cuatro opciones (conservador, liberal, socialista y fascista), que descubriremos más adelante con la información extra del rompecabezas. El segundo cuadrado latino de orden 4 del ejemplo (que junto al anterior cuadrado latino son mutuamente ortogonales) lo vamos a utilizar para las edades (35, 45, 55 y 65) y las denotaremos con letras latinas minúsculas (a, b, c d), que nos interesa que ambos cuadrados latinos sean mutuamente ortogonales ya que ninguno de los pasajeros comparte nacionalidad, estado civil, simpatías políticas y edades. Finalmente, el tercer cuadrado latino, que junto a los otros dos son mutuamente ortogonales, lo utilizaremos para las profesiones (abogado, soldado, médico y clérigo) y las denotaremos con las letras latinas mayúsculas (A, B, C, D). Todo esto lo podemos resumir en la siguiente imagen.

Pero el rompecabezas nos da algo más de información:

“Se sabe que tres de los fascistas son un abogado inglés soltero de 65 años, un militar escocés casado de 55 años y un médico irlandés viudo de 45 años. Es fácil entonces precisar el fascista restante.

Además, el socialista irlandés tiene 35 años, el conservador de 45 años es escocés y el inglés de 55 años es clérigo. ¿Qué sabes del abogado galés?”

Esta información nos va a permitir conocer qué letras representan a qué características. Así, como: i) uno de los fascistas es soltero, inglés, abogado y de 65 años, nos vamos al cuadrado greco-latino generalizado anterior y miramos a la casilla que corresponde con inglés (columna 1) y soltero (fila 4), luego “delta d D”, de donde deducimos que delta = fascista, d = 65 y D = abogado; ii) otro fascista es militar escocés (columna 2) casado (fila 3) de 55 años, de donde sacamos que b = 55 y A = militar; iii) otro es médico irlandés (columna 3) viudo (fila 2) de 45 años, por tanto, a = 45 y C = médico; respecto al cuatro fascista, por el que nos preguntan en el rompecabezas, como no hay dos pasajeros que compartan nacionalidad, estado civil, simpatías políticas, edades y profesiones, entonces tiene que ser divorciado (fila 1), galés (columna 4), clérigo y de 35 años, de donde c = 35 y B = clérigo.

Las asignaciones que faltan, para las letras griegas, la sacamos de la información restante. El socialista irlandés (columna 3) tiene 35 años (c), luego como en la columna 3 la casilla con una c es “beta c A”, entonces beta = socialista; además, el socialista irlandés que tiene 35 años es militar y está soltero. Como el conservador de 45 años (a) es escocés (columna 2), luego miramos la columna 2, la casilla con la letra a, que es “gamma a B”, de donde, gamma = conservador; y podemos completar su información conservador, escocés, 45 años, clérigo y soltero. Ya solo nos falta saber a qué corresponde alpha, que por descarte es alpha = liberal.

Recogiendo toda esta información en el retículo cuadrado tenemos:

La pregunta del rompecabezas es “¿Qué sabes del abogado galés?”. Si tenemos en cuenta que abogado es la letra D y galés es la columna 4, vamos a la casilla que tiene la letra D en la columna 4, que es “beta a D”, en la fila 3, de donde deducimos que:

¡el abogado galés es socialista, está casado y tiene 45 años!

Para terminar solo me queda animaros a que volváis a ver la obra textil The Welsh Lawyer (el abogado galés), de Stephen Threlkeld, que la disfrutéis y que comprobéis que efectivamente es el cuadrado greco-latino generalizado de tres cuadrados latinos de orden 4 mutuamente ortogonales.

Bibliografía:

1.- Raúl Ibáñez, Cayley, el origen del algebra moderna, RBA, 2017.

2.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

3.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, Catarata, 2023 (pendiente de publicación).

4.- Stephen Threlkeld, comunicación privada

5.- Página web del artista Stephen Threlkeld

6.- Ronald A. Fisher, The Designs of Experiments, Oliver and Boyd, 1935.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica