Acabamos de estrenar el año 2023. Este será el Año Internacional del Mijo, un cereal de alto contenido proteico, que puede crecer con poca agua y se adapta a los cambios climáticos. También será el Año Internacional del Diálogo como Garantía de Paz.

En 2023 celebraremos el centenario del nacimiento de importantes figuras de las matemáticas como Armand Borel, Yvonne Choquet-Bruhat, Lloyd Shapley, Cathleen Synge Morawetz o Réné Thom.
El número 2023 (7 x 172) es un número defectivo (el 1521 de la lista de tales números) porque sus divisores son 1, 7, 17, 119, 289 y 2023, y la suma de todos ellos es 2456 (que es menor que 2 x 2023 = 4046). Además, es un número odioso (el 1012 de la lista de tales números) ya que, en base 2, 2023 se escribe como 11111100111 que posee nueve (un número impar) unos. Pero también es un número de la suerte (el 279 de la lista de tales números)… no parece un “mal” número después de todo.
Os proponemos debajo tres problemas de matemáticas que involucran al 2023. ¡Intentad solucionarlos antes de consultar la respuesta!
Un problema de sumas
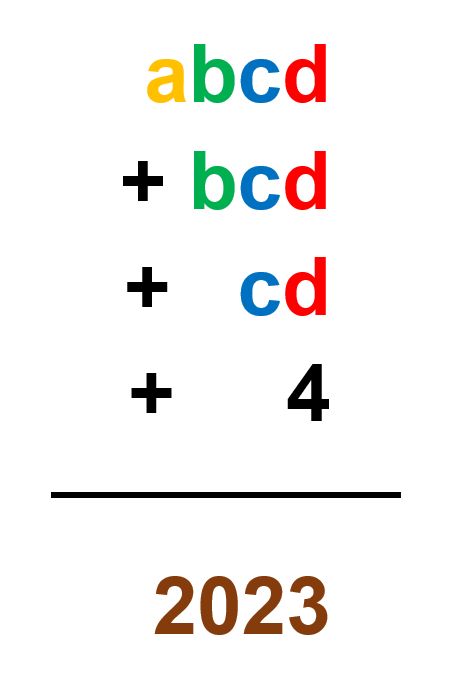
Tenemos un número N de 4 cifras: N = abcd (el dígito a toma valores entre 1 y 9; los dígitos b, c y d toman valores entre 0 y 9).
Si se suman los números abcd + bcd + cd + 4, se obtiene el número 2023. ¿Quién es N?
Solución
La suma abcd + bcd + cd es 2019, con lo que 3d es un número que finaliza en 9. La única posibilidad es que 3d = 9, con lo que d = 3.
Prosiguiendo con las decenas, 3c es un número que finaliza en 1. La única posibilidad es que 3c = 21; es decir, c = 7.
En el caso de las centenas 2b + 2 = 0 (el 2 corresponde a la llevada de las decenas). Hay dos posibilidades: que 2b + 2 = 10 (luego, b = 4) o que 2b + 2 = 20 (luego, b = 9). Pero b no puede ser 9, porque si 2b + 2 = 20, entonces a = 0, y esto es imposible. Así, b = 4.
Como 2b + 2 = 10, se deduce que a + 1 = 2 y, por lo tanto, a = 1.
Luego el número buscado N es 1473.
Un problema de pares de números enteros positivos
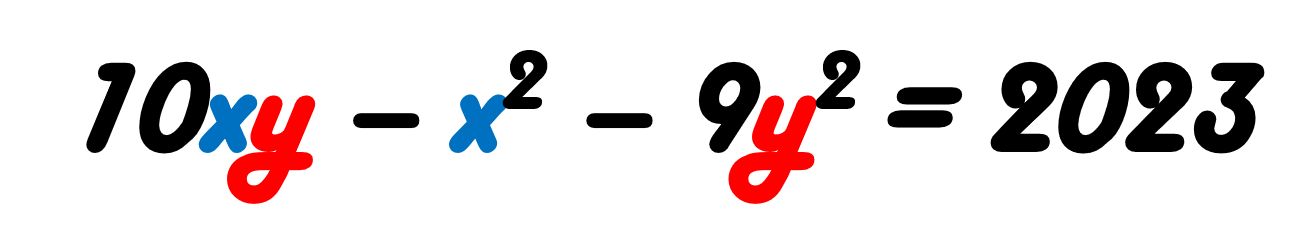
¿Cuáles son todos los pares de enteros positivos (x,y) que verifican la ecuación:
10xy – x2 – 9y2 = 2023?
Solución
Manipulamos la ecuación 10xy – x2 – 9y2 = 2023 y sacamos factor común de diferentes maneras, como se muestra debajo:
xy – x2 + 9xy – 9y2 = 2023,
x (y – x) + 9y (x – y) = 2023,
(x – y) (–x + 9y) = 2023.
Como hemos comentado antes, 2023 factoriza en factores primos como el producto de 7 por 172. Además
(x – y) + (–x + 9y) = 8y.
Por lo tanto, debemos escribir 2023 como el producto de dos números enteros ab (a = x – y y b = –x + 9y) cuya suma a + b sea, además, un múltiplo de 8.
Hay tres posibilidades:
-
Los factores son 7 y 172 = 289. En tal caso, 7 + 289 = 296 = 8y. Por lo tanto, y = 37. Hay dos posibles casos: x – 37 = 7 (x = 44) o x – 37 = 289 (x = 326).
-
Los factores son 17 y 119 (7 por 17). En tal caso, 17 + 119 = 136 = 8y. Por lo tanto, y = 17. Hay dos posibles casos: x – 17 = 17 (x = 34) o x – 17 = 119 (x = 136).
-
Los factores son 1 y 2023. En tal caso, 1 + 2013 = 2024 = 8y. Por lo tanto, y = 253. Hay dos posibles casos: x – 253 = 1 (x = 254) o x – 253 = 2023 (x = 2276).
En resumen, hay seis pares (x,y) de enteros positivos que cumplen la ecuación planteada: (44,37), (326,37), (34,17), (136,17), (254,253) y (2276,253).
Un problema de diferencias

Consideramos las dos sumas siguientes:
a = 12 + 22 + 32 + 42 + … + 20222 + 20232
y
b = (1 x 3) + (2 x 4) + (3 x 5) + (4 x 6) + … + (2022 x 2024).
¿Cuánto vale a – b?
Solución
La diferencia buscada puede reescribirse agrupando términos del modo:
a – b = 12 + 22 + … + 20222 + 20232 – (1 x 3) – (2 x 4) –… – (2021 x 2023) – (2022 x 2024)
= 1 (1 – 3) + 2 (2 – 4) + 3 (3 – 5) + … + 2022 (2022 – 2024) + 20232
= –2 (1 + 2 + 3 + … + 2022) + 20232.
Aplicamos la fórmula de la suma de los n primeros números naturales (para n= 2022), y se obtiene que:
1 + 2 + 3 + … + 2022 = ½ (2022 x 2023).
Sustituyendo arriba tenemos que:
a – b = –2 x ½ (2022 x 2023) + 20232 = –(2022 x 2023) + 20232
= 2023 (–2022 + 2023) = 2023.
¡La diferencia buscada es justamente 2023! ¡Feliz 2023!
Referencia:
Estas tres propuestas (con alguna pequeña modificación) se han extraído del Calendrier Mathématique 2023. Structurer le monde (Presses Universitaires de Grenoble, 2022). Son los desafíos formulados los días 5 de enero, 27 enero y 26 de abril.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

Tres retos matemáticos con el núm…
[…] Estrenamos año 2023 con tres problemas de matemáticas que involucran al número 2023. ¡Intentad solucionarlos antes de consultar la respuesta! […]