no lineal

Aunque el origen de la Dinámica se fundó a partir de los experimentos de Mecánica efectuados por Galileo Galilei, el cálculo infinitesimal -inventado por Isaac Newton y Gottfried Leibniz- permitió describir matemáticamente la evolución general de algunas de las más relevantes magnitudes de todas las ciencias. Las maravillosas ecuaciones diferenciales nos permiten describir, predecir e incluso controlar la dinámica de sistemas no sólo basados en las leyes de la mecánica clásica o relativista, el electromagnetismo o la mecánica cuántica, sino en todas las ciencias naturales y sociales, así como en todas las ingenierías.

El gran Henri Poincaré estableció a finales del siglo XIX las propiedades cualitativas de la teoría de ecuaciones diferenciales, con la Mecánica Celeste [1] como ejemplo de aplicación, pero más allá de esto, estableció su teoría matemática generalizada para fundar la Ciencia General de la Dinámica de Sistemas, aplicable a modelar, predecir su evolución en el tiempo y caracterizar las propiedades esenciales de cualquier efecto medible en cualquier tipo de realidad científica.

El principio de superposición

La mayoría de los científicos naturales o sociales, muy a menudo consideramos verdadera la hipótesis de que la respuesta neta causada en un sistema por dos o más estímulos es la suma de las respuestas que habría causado cada estímulo por separado. Esto es el Principio de Superposición, que parece ser una cuestión casi de sentido común, y que muchas veces la asumimos sin demasiadas cautelas.

Una función matemática que satisface el principio de superposición se denomina función lineal. Estas funciones lineales, muy utilizadas con gran generalidad en todas las ciencias, incorporan dos propiedades matemáticas muy útiles como la aditividad y la homogeneidad, y nos permiten un análisis e interpretación muy profunda -y bastante sencilla- de leyes que establezcamos, experimentos que realicemos, generalizaciones que propongamos o conclusiones que extraigamos de una investigación.

El principio de superposición se aplica a cualquier sistema lineal, descrito mediante ecuaciones algebraicas o ecuaciones diferenciales lineales. Los estímulos sobre un sistema y las respuestas de éste pueden ser números, funciones, vectores, campos vectoriales, señales variables en el tiempo o cualquier otro objeto que cumpla ciertos axiomas muy comunes. Los Sistemas Lineales son una de las maneras más utilizadas para describir la realidad, aún estudiando situaciones complejas, como aquellas basadas en las leyes de Newton, las ecuaciones de Maxwell, la ecuación de Schrödinger o modelos en econometría, ecología, o cualquier tipo de ciencia para la que tratamos de expresar matemáticamente su funcionamiento. Una ventaja que tenemos es que, cuando escribimos un estímulo muy general en un sistema lineal como la superposición de estímulos de una forma específica y simple, a menudo la respuesta global resulta más fácil de calcular y predecir.

Modelos lineales ordinarios o extraordinarios

Muchos sistemas dinámicos, basados en algunas de las leyes más valiosas de la historia de la ciencia, se pueden expresar mediante ecuaciones diferenciales ordinarias lineales con coeficientes constantes. Los matemáticos han suministrado para este tipo de sistemas -llamados autónomos- un verdadero arsenal de medios para resolverlos analíticamente, por muy complejos éstos sean. Por ejemplo, la conocida Transformada de Laplace reduce un complejo sistema de ecuaciones diferenciales ordinarias lineales en un sistema de ecuaciones algebraicas, mucho más fácil de solucionar. Ello además nos permite nos solo conocer al dedillo la evolución en el tiempo del sistema dinámico que hemos resuelto, sino también descubrir sus sorprendentes propiedades en el dominio de la frecuencia, extrayendo nuevo conocimiento que no pensábamos obtener de la mera integración de una sencilla ecuación diferencial.

Las ecuaciones diferenciales ordinarias son un caso particular de las ecuaciones en derivadas parciales, muy comunes también para describir la dinámica en todas las ciencias, y que, en contraposición con las anteriores más sencillas descripciones ordinarias, podemos denominar modelos extraordinarios. Aunque su resolución en este caso es algo más compleja, las ecuaciones diferenciales lineales, sean ordinarias o no, permitieron a los físicos expresar asuntos clave como la dinámica de los planetas, todo el electromagnetismo o la dualidad onda-corpúsculo, entre muchas otras cuestiones. Hoy día científicos e ingenieros de toda especie establecen modelos dinámicos para explicar por qué ocurre la realidad experimentada en su propio ámbito.

La realidad es no lineal

Muy pocos científicos utilizan ecuaciones diferenciales no lineales. Sentimos una cierta reacción alérgica a su empleo, quizás por la dificultad de resolver la matemática de estas ecuaciones o quizás por abandonar el principio de superposición que tanto apreciamos. En la teoría general de relatividad de Albert Einstein, las ecuaciones son no lineales, y su resolución casi siempre implican métodos matemáticos de linealización o de perturbaciones. Incluso para sistemas mucho más sencillos, descritos en simples ecuaciones diferenciales ordinarias no lineales, nuestra tendencia es linealizar el sistema en torno a unas ciertas condiciones y resolver ecuaciones lineales, para tratar de extraer información -al menos parcial- de la realidad que hemos modelado.

La cuestión es que la realidad es no lineal, y nuestras ecuaciones lineales pueden modelar bastante bien las cosas, pero en ocasiones ocurren fenómenos muy imprevisibles y no intuitivos, tanto en las ciencias naturales como en las ciencias sociales o en las ingenierías. Estos fenómenos no se producen en los modelos lineales, y son por tanto exclusivos de los sistemas no lineales.

Múltiples puntos de equilibrio

Los puntos de equilibrio son las soluciones constantes en una ecuación diferencial. En sistemas lineales autónomos, el modelo tiende a un único punto de equilibrio. Uno de los ejemplos más sencillos podemos encontrarlo en la aproximada ley de enfriamiento de Newton: una simple ecuación diferencial lineal de primer orden que explica la transferencia de calor entre dos cuerpos partiendo de diferentes temperaturas. El punto de equilibrio es único y establece igualdad de temperaturas entre ambos cuerpos.

Si a esta sencilla ecuación diferencial añadimos un simple término cuadrático nos encontramos con un básico sistema no lineal, cuya resolución numérica puede observarse en la Figura 1.

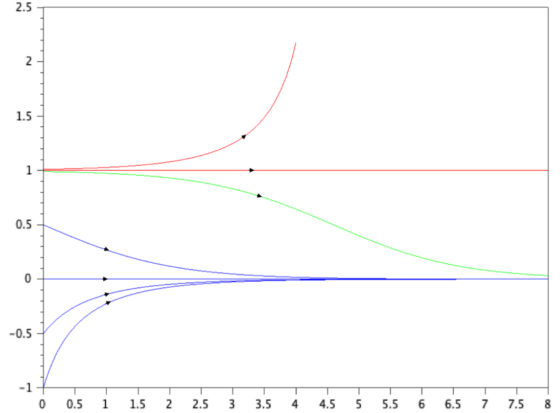
Vemos que linealizando el sistema en torno a la temperatura 0, la solución (trayectorias azules) tienden al punto de equilibrio previsto por la ley de enfriamiento de Newton, si partimos de las inmediaciones en torno a la cual hemos linealizado. Pero si resolvemos el sistema no lineal completo, descubrimos que partir de otras condiciones iniciales nos puede dar lugar a otras soluciones radicalmente diferentes causadas por un segundo punto de equilibrio en 1. Cualquier perturbación partiendo de esta segunda temperatura hace que el sistema abandone la situación y, o bien tienda al anterior equilibrio 0 (trayectoria verde), o bien la temperatura crezca sin límite (trayectoria roja).

Ciclos límite

Los sistemas no lineales pueden oscilar sin excitación externa, con amplitud y frecuencia fijas. Las oscilaciones lineales como por ejemplo las de un péndulo linealizado en torno a la vertical, puede cambiar la amplitud de sus oscilaciones (por ejemplo, empujando más o menos un columpio). Balthasar Van der Pol, hacia 1920, añadió un término no lineal a la ecuación diferencial lineal del péndulo, haciendo depender su coeficiente de amortiguamiento con su posición. Se trata entonces de una sencilla ecuación diferencial ordinaria no lineal de segundo orden.

En sistemas dinámicos de orden dos o superior, se emplea muchas veces el espacio de fases para representar los grados de libertad del sistema. En la Figura 2 se muestra la solución de la ecuación de Van der Pol con dos condiciones iniciales diferentes.

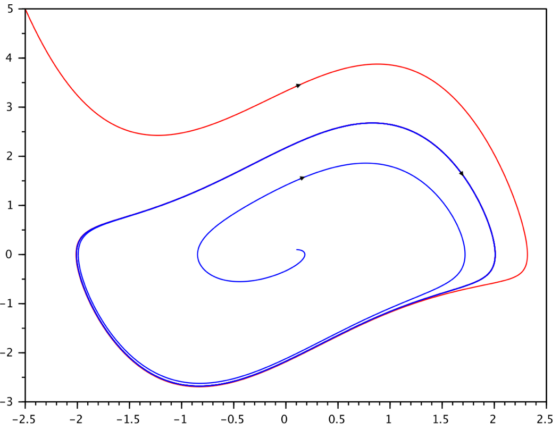
Partiendo de posición y velocidad pequeñas (trayectoria azul inicialmente cerca de cero en la Figura 2), el sistema amplifica su oscilación sin excitación externa y tiende a cierta frecuencia y amplitud fijas (ciclo cerrado azul). Partiendo de posición y velocidad amplias (trayectoria roja) el sistema pierde energía y al final tiende a oscilar exactamente igual. En el plano fásico observamos el ciclo cerrado, llamado ciclo límite, efecto causado por la no linealidad añadida por Van der Pol. Ante cualquier perturbación creciente o decreciente que sufra la posición o velocidad de este especial péndulo no lineal, el dispositivo corregirá la situación y volverá a oscilar a la misma frecuencia y amplitud propias. Se trata de un sorprendente ciclo límite estable, exclusivo de los sistemas no lineales, y que nos lleva a un nuevo concepto de región de equilibrio estable, generalización del concepto de punto de equilibrio estable que hemos descrito arriba.

Caos

En sistemas dinámicos lineales estables, la ligera modificación de sus condiciones iniciales da lugar a ligeros cambios en su respuesta. Sin embargo, en sencillos sistemas no lineales se puede observar una extrema sensibilidad a las condiciones iniciales, propiedad exclusiva de la no linealidad, y que se denomina caos.

En la Figura 3 se muestran las soluciones de una ecuación diferencial ordinaria no lineal de segundo orden que modela un sistema mecánico con deflexiones elásticas no lineales y forzado con un coeficiente no constante ([2] p.7).

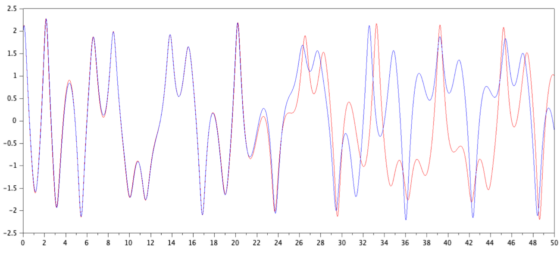
Puede observarse que, ante condiciones iniciales casi idénticas, las dos trayectorias del sistema (azul y roja) son al principio iguales, pero en pocos instantes se produce una bifurcación radical en el comportamiento del sistema. Nuestro modelo es totalmente determinista, su ecuación puede ser exacta, pero su comportamiento es imprevisible: muy parecido a la imposible previsión del tiempo atmosférico que conocemos. Este ejemplo es aún más sencillo que el famoso modelo de dinámica atmosférica que presentó el conocido matemático y meteorólogo Edward Lorenz. En la Figura 4 se muestra una implementación física del atractor de Lorenz y su medida caótica en el laboratorio.

La dinámica de la naturaleza y las sociedades es inherentemente no lineal. Los sistemas lineales deben entenderse como caso particular de los más generales sistemas no lineales. Los fenómenos impredecibles, anti-intuitivos o sorprendentes los podemos modelar, explicar, predecir, experimentar y controlar en el laboratorio, así como tratar de contribuir a descubrir o solucionar los enigmas de lo que llamamos realidad.

Referencias

[1] Henri Poincaré (1892-1893-1899) Les méthodes nouvelles de la mécanique céleste TOME I, II et III (PDF). Gauthier-Villars et fils, Paris

[2] Victor Etxebarria (1999) Sistemas de control no lineal y robótica. Servicio Editorial de la UPV/EHU, ISBN 8483731924 – 9788483731925, Bilbao

Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)