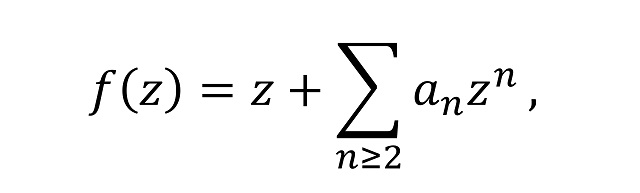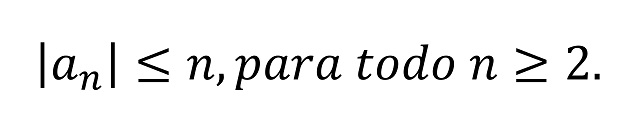Inmersión, un cómic empapado de matemáticas (II)
Como se comentaba en la entrada del Cuaderno de Cultura Científica titulada Inmersión, un cómic empapado de matemáticas (I), las matemáticas están muy presentes, tanto en la historia, como en la estética, del cómic de terror Inmersión (Hill House Comics – DC Black Label; ECC Ediciones, 2021), de Joe Hill (guion), Stuart Immonen (dibujo) y Dave Stewart (color). Esa primera entrega del análisis de las matemáticas del cómic Inmersión se centraba en la parte estética del cómic, tanto en las portadas, como en las páginas de créditos, de los seis números que lo componen.

Antes de introducirnos en el análisis del contenido matemático de esta obra de ficción gráfica, recordemos la temática de la misma. En Inmersión se homenajea al género de terror de los años ochenta, con dos referencias claras, una película clásica de terror de esa década, La cosa (1983), del director estadounidense John Carpenter (1948), y uno de los escritores clásicos de este género, el estadounidense H. P. Lovecraft (1890-1937) y sus mitos de Cthulhu.

Por último, recordemos el tema de esta obra a través de la sinopsis que aparece en la página web de la editorial ECC, que es la siguiente.
En 1983, el Derleth, un buque de perforación de última generación, desaparece cerca del Círculo Polar Ártico. Décadas más tarde empieza a emitir una señal de socorro…
La compañía petrolífera Rococo sigue la señal hasta un remoto atolón del Estrecho de Bering y contrata a los hermanos Carpenter y su tripulación de rescate para investigar el barco fantasma. Junto con una bióloga marina y un ejecutivo petrolífero, los hermanos se embarcan en una siniestra misión para averiguar las causas de la desaparición del barco y recuperar los cuerpos de la tripulación… ¡pero resulta que los hombres del Derleth no están muertos! Aunque tampoco están ya del todo… vivos…
El número pi
Las matemáticas contribuyen a crear el ambiente de terror del cómic. Ya en las portadas y en las páginas de créditos nos encontramos diagramas y símbolos matemáticos, listas de números (los decimales del número pi), así como fórmulas matemáticas pintadas de rojo, como si fuera sangre que está goteando, fórmulas extrañas, raras, frías, sin ningún significado para la persona que lee el cómic. Pero dentro de la historia también nos vamos a encontrar con matemáticas, en gran medida, con el mismo objetivo de contribuir al ambiente de terror del cómic.
Cuando el barco del capitán Carpenter, contratado para rescatar el buque Derleth, llega a la isla donde se encuentra encallado el buque, varios de los miembros de la tripulación se dedican a explorar la isla (en el número #2 del cómic). Dos de ellos, que están explorando por el interior de la misma, se encuentran con algunos números marcados en una piedra a la entrada de una cueva. Quien los ha encontrado le dice a su compañero “Aquí ha estado alguien. Mira. Números”. Los números que vemos en el dibujo del cómic son “3,14159” y el descubridor del número comenta que podría ser el número pi (para más información sobre esta importante constante matemática puede leerse la entrada ¿Es normal el número pi?). Entonces, decide explorar la cueva para ver si hay rastro de los miembros de la tripulación del Derleth y va descubriendo que “los números siguen”, es decir, sigue habiendo números en piedras encontradas a lo largo de la cueva. Esta es la conversación entre el tripulante que está dentro la cueva y su compañero que le espera en el exterior, al descubrir que hay números grabados en el interior.
– Los números siguen. Me pregunto si serán correctos. ¿No había un concurso para ver hasta dónde podían calcular el número pi los ordenadores?
– No lo sé. Sí. A lo mejor. ¿Hasta dónde llega el agujero de las mates?
– Creo que va desde algebra de primero hasta trigonometría avanzada. Y si te soy sincero aprobé precálculo raspado y nunca llegué a …
– ¿Russ? Tal vez deberías volver. ¿Russ?

Antes de continuar, podemos comentar que efectivamente, desde la antigüedad se intentan calcular los decimales del número pi. Si hubiese sido un número racional tendría un número finito de decimales o existiría un número finito que se repetiría periódicamente de forma infinita, sin embargo, desde 1761 se sabe que este número tiene infinitos decimales y no hay ningún patrón que se repita, ya que el número pi es irracional, como demostró el matemático alemán Johann H. Lambert (1728-1777) ese año.
A partir de ese momento, empezó la carrera para intentar calcular la mayor cantidad posible de decimales de este número irracional. En aquel tiempo se conocían muy pocos decimales. Por ejemplo, el matemático japonés Yoshisuke Matsunaga (c.a. 1694-1744) había calculado 51 decimales del número pi en 1739, mientras que el matemático esloveno Jurij B. Vega (1754-1802) calculó 140 decimales en 1789, aunque solo los 126 primeros eran correctos. Estos cálculos se realizaban a mano.
Hubo que esperar hasta mucho tiempo después, 1949, para superar los mil decimales, en concreto, 1.120 decimales correctos del número pi, que fueron calculados con la ayuda de una simple calculadora por los matemáticos estadounidenses Levi B. Smith y John Wrench (1911-2009). A partir de ese momento llegó la era de los ordenadores y empezaron a conocerse cada vez más decimales.
En 1961, de nuevo el matemático estadounidense John Wrench, junto a su colega Daniel Shanks (1917-1996), haciendo uso de un ordenador IBM7090, calcularon ya más de 100.000 decimales del número pi. Con el paso de los años la cantidad de decimales calculados fue creciendo cada vez más. El billón de decimales se superó en 2002, por un equipo formado por el experto en ciencias de la computación japonés Yasumasa Kanada (1949-2020), utilizando un ordenador HITACHI SR8000.
El último récord en el cálculo de los decimales del número pi es de 300 billones (300.000.000.000.000) de decimales, resultado de la colaboración entre la multinacional japonesa fabricante de memorias para ordenadores KIOXIA y la empresa canadiense Linus Media Group, que se ha obtenido hace un mes, en abril de 2025.
Pero volvamos al punto en el que lo dejamos en el cómic. El tripulante del barco de rescate Russ continúa bajando por la cueva y encontrando números grabados en la piedra de las paredes.
– ¡Eh, Bill! ¡Bill! Tendrías que ver esto …
… Esto sigue y sigue. Bill, me parece que alguien se ha pasado mil pueblos resolviendo el número pi …
… ¡Eh, Bill! Podríamos llamar a este sitio Fraggle Rock. ¡Hay matemáticas, y también dibujo! O a lo mejor mitología, no lo sé.
Entonces, llega a un símbolo circular con una especie de “bichos” alrededor, que podemos ver en la siguiente imagen.

Los infinitos decimales del número pi
Sin embargo, las menciones al número pi no terminan ahí. En el número #3 de Inmersión Russ, después del descubrimiento sobre el número pi, se encuentra con varios de los tripulantes del desaparecido buque Derleth, que podríamos decir que no están vivos, pero tampoco muertos. Por cierto, cuando Russ descubre a los tripulantes del Derleth le pregunta a uno de ellos, que se presenta como Julian, cuántos son, pero este le contesta “Esa no es una pregunta sencilla. Hay matemáticas complejas y matemáticas sencillas”, respuesta que esconde parte del misterio de la historia.
En la posterior conversación de estos misteriosos y aterradores tripulantes del Derleth con los tripulantes del barco de rescate se mencionan más matemáticas, que comentaremos más adelante, pero en particular se vuelve a mencionar el número pi.

El siguiente trozo de conversación tiene lugar entre el “no vivo-no muerto” primer oficial del Derleth, Julian Foyle, y un empleado de la compañía petrolífera Rococo, dueña del Derleth, David Lacome.
[DL]: Era una invitación, por supuesto. Pensé … pensé que prometía algo más. ¿Hay algo más, Sr. Foyle?
[JF]: Oh … sí … en la cueva … en la colina … hemos resuelto … el número pi hasta el final.
[DL]: Eso … es imposible … pi no tiene fin.
[JF]: Oh, sí que lo tiene. Y ver … el número entero … es ver el universo … como el Dios … de Cristo … y Judas Iscariote … lo vería … de no haber muerto hace tiempo …
… Hemos demostrado … la veracidad de la Hipótesis de Riemann… y confirmado … la conjetura de Crouzeix …
… Pero esos … no … son más … que juegos … de niños … dependen de la geometría euclidiana … y su … apego imperfecto … a un universo racional … podemos ofrecerle mucho más …
Cuando el “no vivo-no muerto” primer oficial del Derleth, Julian Foyle, afirma que “hemos resuelto el número pi hasta el final” y “el número entero” se refiere a que conocen todos los infinitos decimales del número pi, aunque estos sean infinitos.
Tanto estas menciones al número pi, la Hipótesis de Riemann o la conjetura de Crouzeix, así como la conjetura de Milin, que se menciona un poco antes, intentan transmitir que esos “seres” (lo que sea que está ocurriendo con los tripulantes del Derleth, que no vamos a desvelarlo en esta entrada) son extremadamente inteligentes.
Por otra parte, la mención a la geometría euclideana es otro pequeño homenaje al escritor H. P. Lovecraft, y sus mitos de Cuthulu, en particular, al relato La llamada de Cthulhu (1926). Como se mencionó en la primera entrega de esta serie, Inmersión, un cómic empapado de matemáticas (I), el propio Joe Hill menciona la ciudad submarina de R’lyeh, un lugar ficticio de los mitos de Cthulhu, como un punto de partida en su relato de horror, y de ella se dice en el relato anterior que “la geometría de la ciudad de sus sueños era anormal, no euclidiana, y que sugería esferas y dimensiones distintas de las nuestras”.
De conjeturas, hipótesis y teoremas
Al inicio del número #3 del cómic Inmersión, nos muestran como la capitana del Derleth fue encontrada por un pescador en un bote salvavidas. Ella, que estaba muerta, tenía en su mano un papel (como se puede ver en la siguiente imagen) con una fórmula matemática y un número, el “01134”.
– Siete meses después de que el Derleth desapareciera, el cuerpo de la capitana reapareció en un bote al norte de Nome. Junto a su cuerpo se descubrió una fórmula que confirmaba la conjetura de Milin … una propuesta sobre coeficientes logarítmicos. Los detalles no importan. Lo importante es que los cálculos de Lucas resolvían un problema que tenía desconcertados a los matemáticos desde hacía años.
Más adelante en ese mismo número del cómic, David Lacome, empleado de la compañía petrolífera Rococo, habla de esa fórmula.

La verdad es que me sorprendió la mención a la conjetura de Milin, puesto que no es una conjetura muy famosa, como pueden ser la conjetura de Poincaré, la hipótesis de Riemann (esta sí es mencionada en el cómic) o la conjetura de Hodge, que son tres problemas abiertos (bueno, la conjetura de Poincaré fue resuelta en 2003 por el matemático ruso Gregori Perelman, y que también está recogido en un cómic como se puede leer en la entrada La conjetura de Poincaré-Perelman-Miander), que pertenecen a la colección de los siete problemas del Milenio, dotados con un premio de un millón de dólares para quienes los resuelvan, u otros famosos problemas abiertos, como la conjetura de Goldbach (para saber más sobre esta léase la entrada La conjetura de Goldbach).
La conjetura de Milin era una conjetura, relacionada con otra conjetura, la de Bieberbach, que pertenecen a una rama de las matemáticas conocida como análisis complejo o teoría de las funciones de variable compleja. Estas dos conjeturas no son sencillas de entender, salvo que sepas un poco de matemáticas, por lo que no voy a intentar explicarlas aquí. Aunque sí quiero escribir el enunciado de la primera para que se entienda la dificultad. La conjetura de Bieberbach fue propuesta por el matemático alemán Ludwig Bieberbach (1886-1982) en 1916.
Conjetura de Bieberbach: Si f es una función holomorfa inyectiva definida del disco unidad en el plano complejo, cuya serie de Taylor es de la forma
normalizada en el sentido de que a0 = 0 y a1 = 1, entonces
La conjetura de Milin, que fue propuesta por el matemático ruso (soviético) Isaak M. Milin (1919-1992), en 1977, implicaba la conjetura de Bieberbach. De hecho, la conjetura de Milin fue demostrada por el matemático franco-estadounidense Louis de Branges de Bourcia (1932) en 1985, con lo que quedaba probada la más famosa conjetura de Bieberbach.
Si leemos en la Wikipedia la entrada “De Branges’s theorem” podemos ver en la parte de la demostración de Louis de Branges de la conjetura de MIlin la siguiente expresión matemática
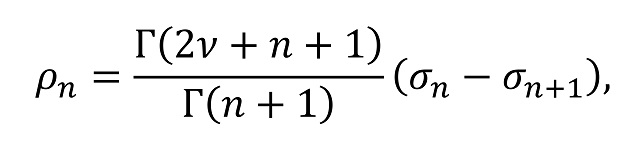
que no voy a intentar explicar aquí, pero que, si os fijáis, es la expresión matemática que estaba en el papel que agarraba el cuerpo sin vida de la capitana del Derleth cuando fue encontrada poco después de la desaparición de su barco, en 1983. Hemos de notar que la demostración de de Branges de la conjetura de Milin fue posterior a esa fecha, dos años después, en 1985.
Otras dos conjeturas se mencionan en este cómic, la conjetura de Crouzeix y la Hipótesis de Riemann. La primera es un problema abierto que pertenece a la rama de las matemáticas conocida como análisis matricial, que se ocupa del estudio de las propiedades algebraicas de las matrices. Esta conjetura fue propuesta por el matemático francés Michel Crouzeix en 2004 y, aunque se ha avanzado en la misma, todavía es un problema abierto.
Por otra parte, como decíamos, la hipótesis de Riemann sí es un problema matemático abierto muy conocido. Para quien quiera conocer, de forma sencilla, un poco más sobre esta conjetura, puede leer la entrada Los humanos, un Macguffin matemático.
Un chiste matemático
La última referencia matemática que voy a comentar es un pequeño chiste matemático, bastante infantil, comparado con todo lo demás que se ha comentado.
Cuando el cuerpo sin vida de la capitana del Derleth aparece en el bote salvavidas con el papel en la mano, este contiene la “solución” a la conjetura de Milin, que ya hemos comentado, y un número “cero-uno-uno-tres-cuatro”, que puede verse en la siguiente imagen.

Cuando este papel llega a David Lacome, que recordemos que es un empleado de la compañía petrolífera Rococo, dueña del Derleth, este descubre que se trata de un chiste matemático, ya que el número girado y puesto del revés resulta ser la palabra “hello” (véase la siguiente imagen), luego es un mensaje de contacto, aunque no sabemos de quien.

Como se dice en la versión en español, si se marca en una calculadora el número 50538 y se gira la calculadora, se puede leer “besos”. La verdad es que el mensaje es muy infantil comparado con el resto, como si los humanos fuéramos un poco tontos y no pudiéramos entender un mensaje más complejo.

Para terminar, recomendaros que leáis el cómic de terror Inmersión (Hill House Comics – DC Black Label; ECC Ediciones, 2021), de Joe Hill (guion), Stuart Immonen (dibujo) y Dave Stewart (color).
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica