El problema de Malfatti
Leyendo estos días sobre uno de los matemáticos más prolíficos de todos los tiempos, justo por detrás de Leonhard Euler (1707-1783) y Augustin Louis Cauchy (1789-1857), y el matemático puro por excelencia en la Gran Bretaña del siglo XIX, Arthur Cayley (1821-1895), he descubierto que trabajó en un curioso, y popular, problema de geometría euclídea conocido como el problema de Malfatti.

Gian Francesco Malfatti (1731-1807) fue un matemático italiano que trabajó en diferentes áreas de las matemáticas, álgebra, análisis, mecánica, geometría y teoría de la probabilidad. Fue catedrático de Matemáticas e Hidrostática de la Universidad de Ferrara, uno de los fundadores de la Società Italiana delle Scienze (1782), así como uno de los participantes más activos del proyecto de la Nuova Enciclopedia Italiana (1779), que surgió siguiendo el mismo espíritu de la Encyclopèdie francesa, editada por Diderot y D’Alambert.
Es conocido principalmente por el problema que lleva su nombre, el problema de Malfatti, que planteó y solucionó en su artículo Memoria sopra un problema stereotomico (es decir, Memoria sobre un problema estereotómico), publicado en 1803 en la Memoria di Matematica e Fisica della Società Italiana delle Scienze.
Según el diccionario de la lengua española de la RAE, la estereotomía es “el arte de cortar piedras y otros materiales para utilizarlos en la construcción”. Así en las primeras líneas del artículo Gian Francesco se plantea el siguiente problema:
Dado un prisma triangular recto de cualquier material, por ejemplo, el mármol, cortar del mismo tres cilindros [circulares] con la misma altura que el prisma, pero con el máximo volumen total, es decir, con el mínimo desecho de material del volumen del prisma.
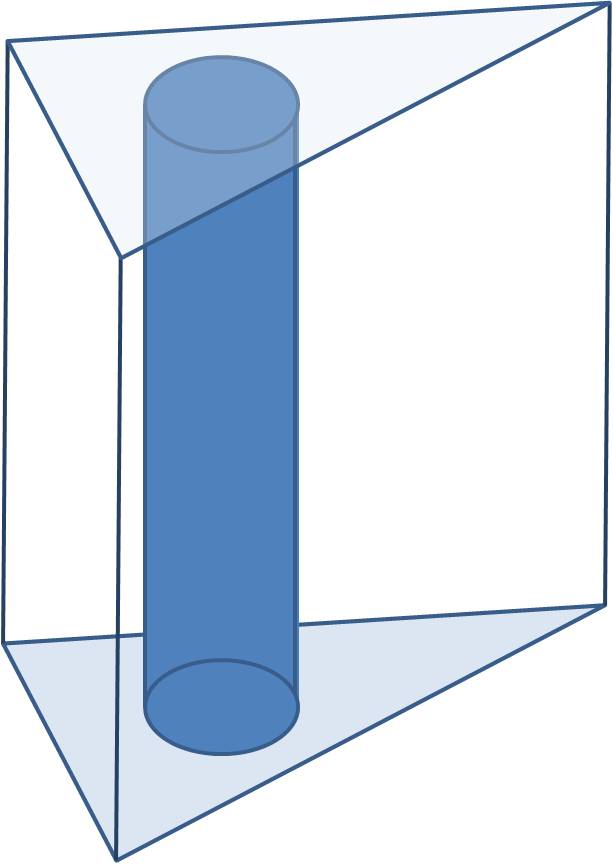
El problema de los tres cilindros dentro del prisma triángular con el mayor volumen posible se puede reducir, como ya observó el matemático italiano en su Memoria sopra un problema stereotomico, a un problema de la geometría plana. En concreto, la cuestión es equivalente al siguiente problema del plano (al que podemos denominar problema original de Malfatti):
Dado un triángulo, encontrar tres círculos, que no se superpongan, dentro del triángulo y que tengan, entre los tres, una superficie máxima.
Además, Malfatti afirma en su trabajo, sin aportar ninguna explicación, que el anterior problema de geometría plana, y por lo tanto su problema sobre el corte de cilindros en el prisma triangular recto, se reduce al siguiente, que es el que se conoce como “problema de Malfatti”:
Problema de Malfatti: Dado un triángulo, construir tres círculos dentro del mismo tal que cada uno de los círculos sea tangente (es decir, se toquen en un punto) a los otros dos y a dos lados del triángulo (a estos se les llama círculos de Malfatti).
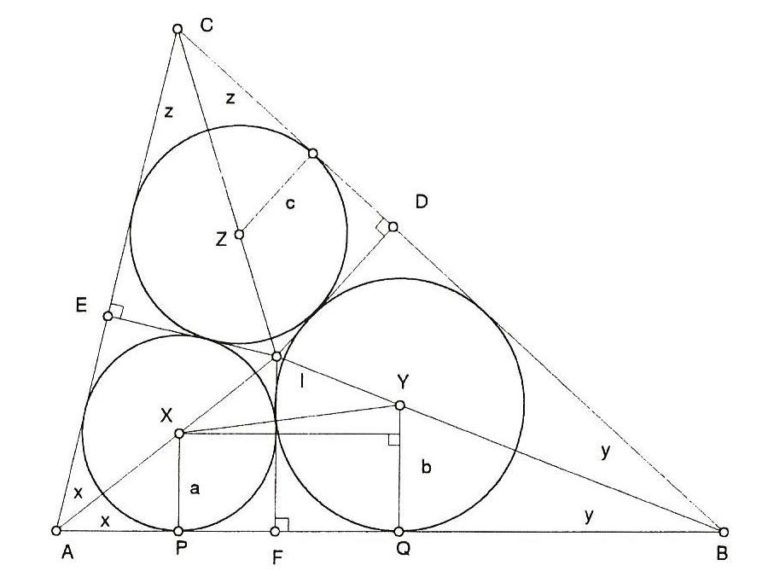
El propio Malfatti resolvió el problema utilizando métodos de geometría analítica. En concreto, el catedrático de la universidad de Ferrara calculó las coordenadas de los centros de los círculos fruto de su construcción. Además, demostró que el problema se puede resolver con regla y compás (la condición de resolver un problema, o construir un objeto geométrico, con la regla y el compás como únicas herramientas viene de la matemática griega antigua, y en ese tiempo se impuso como condición ideal para resolver algunos problemas de la geometría del plano).
A continuación, se muestra el esquema de la demostración del problema de Malfatti que realizó el matemático alemán Karl Schellbach (1804-1892), y cuyos detalles pueden leerse tanto en el libro Geometric Constructions de George E. Martin (al que pertenece la imagen), como en el libro 100 Great Problems of Elementary Mathematics: Their History and Solutions, de H. Dorrie.
La construcción empieza calculando las bisectrices de los ángulos del triángulo, en las cuales estarán los centros de los tres círculos de Malfatti, y el punto en el que se intersecan las bisectrices, el incentro. Después se trazan las alturas desde el incentro a los lados del triángulo, y cada uno de los tres círculos está inscrito en uno de los cuadriláteros que surgen.
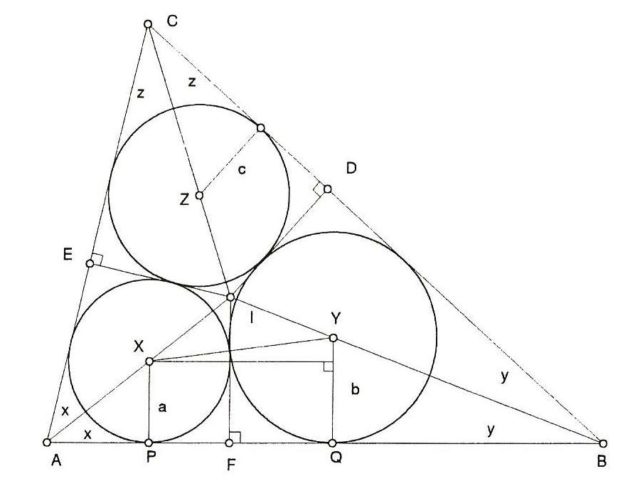
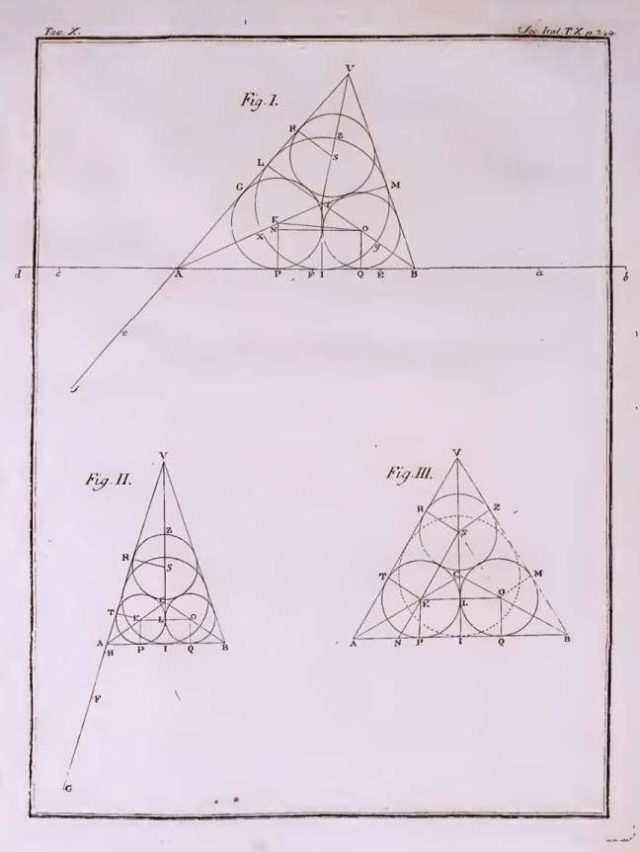
Así mismo, se pueden obtener fórmulas para los radios de los tres círculos, que son tangentes a los otros dos y a dos lados del triángulo. Según Mirolad Stepanovic, en su artículo Triangle centers associated with the Malfatti circles (2003), Malfatto calculó dichas fórmulas, que fueron publicadas, póstumamente, en 1811.
Las fórmulas para los radios están dadas en función de las longitudes de los lados del triángulo a, b, c, la distancia r del incentro a los lados del triángulo (que es la circunferencia de centro el incentro e inscrita en el triángulo), la mitad del perímetro s = (a + b + c) / 2, y las distancias d, e, f del incentro del triángulo a los vértices opuestos a los lados a, b, c:
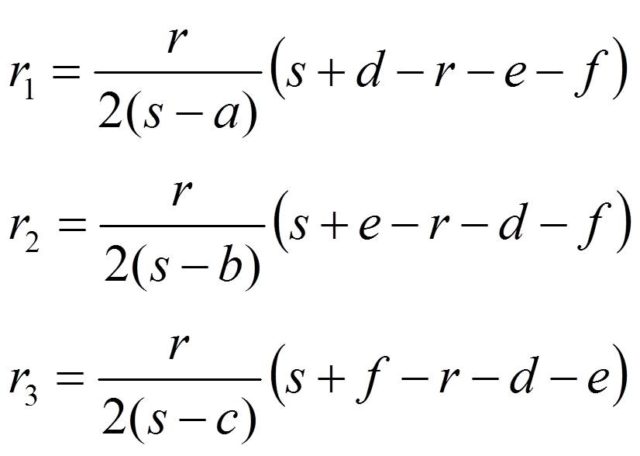
En 1826 el matemático alemán Jakob Steiner (1796-1863) publicó una hermosa solución haciendo uso de la geometría sintética.
A continuación, mostramos un esquema de dicha construcción (las imágenes han sido realizadas con Geogebra en la página www.geogebra.org):
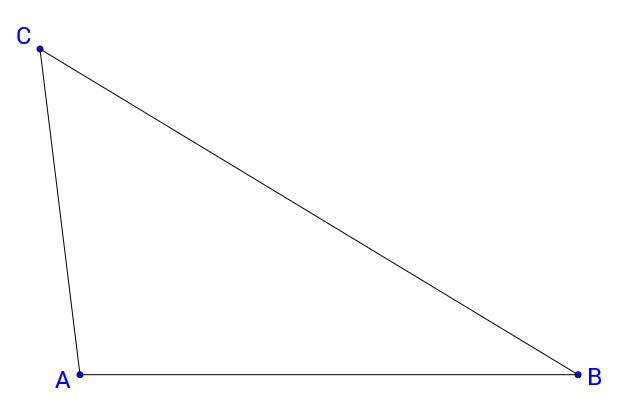
Dado un triángulo ABC, se trazan las bisectrices de los tres ángulos del triángulo (los centros de los círculos de Malfatti están en las bisectrices de los ángulos), que se cortan en el incentro I.
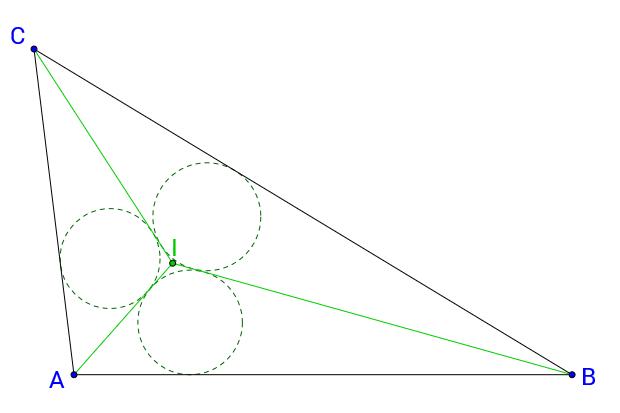
A continuación, se trazan (con trazo discontinuo) los tres círculos inscritos en los triángulos pequeños marcados por las bisectrices, IAB, IBC y ICA. Cada bisectriz es tangente a dos de los círculos trazados (los cuales no se tocan entre sí), pero existe otra recta que también es tangente a cada par de círculos, que se dibuja de color rojo y con trazo discontinuo.
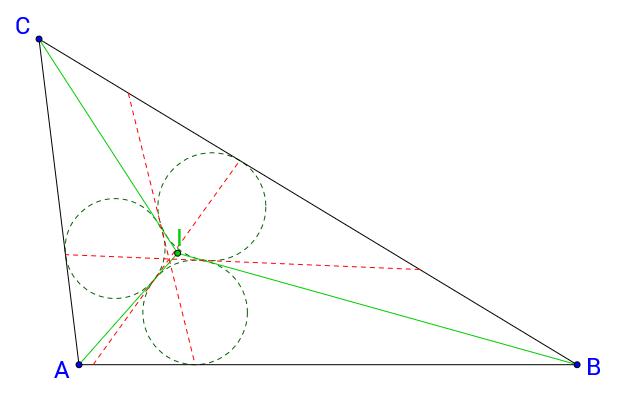
Finalmente, se trazan los tres círculos que están inscritos en cada uno de los cuadriláteros formados por dos de los lados del triángulo y dos de esas rectas que son tangentes a dos de los círculos (y que hemos pintado de rojo y con trazo discontinuo).
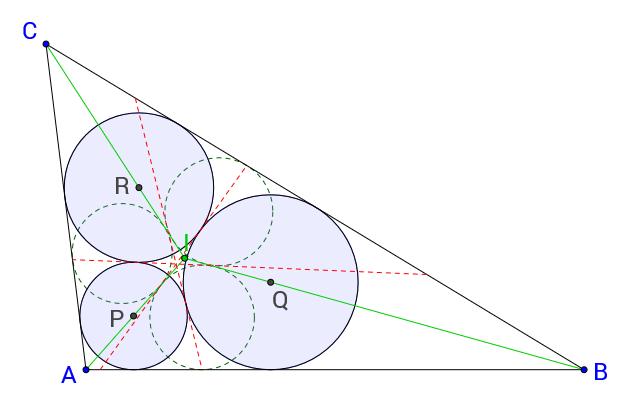
Esos tres círculos son círculos de Malfatti.
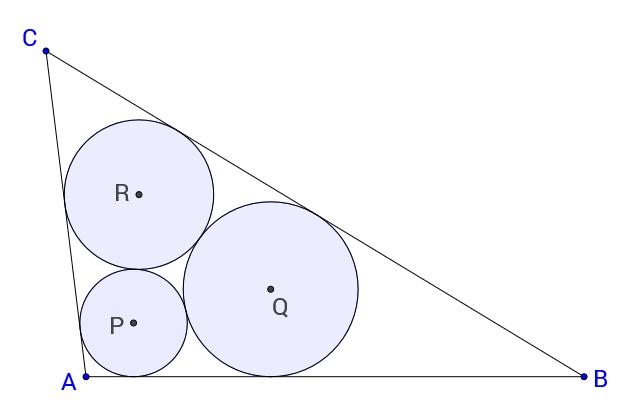
Muchos matemáticos del siglo XIX se interesaron por el problema de Malfatti y trabajaron en generalizaciones del mismo, entre ellos, el inglés Arthur Cayley, los alemanes Karl Schellbach y Alfred Clebsch (1833-1872), o el francés Joseph Diaz Gergonne (1771-1859), por citar algunos.
Al parecer, el problema de Malfatti de construir tres círculos dentro de un triángulo de forma que cada círculo sea tangente a los otros dos círculos y a dos de los lados del triángulo, ya fue propuesto por el matemático japonés Ajima Naonobu (1732-1798) como un sangaku o problema de geometría de los templos japoneses (véase la entrada Sangakus, pasión por los desafíos matemáticos), treinta años antes de que lo hiciera Malfatti.
Volviendo al problema original de Malfatti, es decir, el problema del prisma triangular y los tres cilindros interiores con el mayor volumen posible, y su versión de geometría plana, resulta que contrariamente a lo que afirmaba Malfatti, no es cierto que los círculos que llevan su nombre resuelvan ese problema, es decir, pueden existir tres círculos dentro del triángulo, que no sean de Malfatti y que, sin embargo, cubran una superficie mayor que los de Malfatti.
En concreto, en 1930 los matemáticos H. Lob y H. W. Richmond, en un artículo en el que analizaban las diferentes soluciones existentes al problema de Malfatti, que son 32 soluciones distintas (si se considera el caso general en el que los círculos pueden ser externos y tangentes al triángulo, derivado de la solución algebraica del problema), titulado The soluctions to Malfatti’s problem for a triangle (Proc. London Math. Soc. 2, 30 (1930), 287-304), escribían:
La afirmación de Malfatti sobre cortar cilindros de un bloque de mármol dejando sin utilizar la mínima cantidad de material no está probada. […] En un triángulo equilátero la afirmación no es cierta, para el círculo inscrito en el triángulo, con dos pequeños círculos apretados contra dos ángulos, estos contienen una superficie mayor que los círculos de Malfatti.
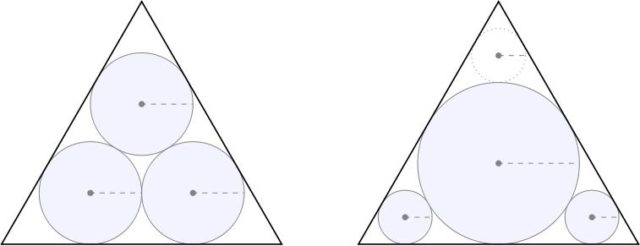
De hecho, puede demostrarse (véase por ejemplo el artículo de Michael Goldberg, On the original Malfatti Problem) que si se toma un triángulo equilátero de lado 2 cm (cuyo área sabemos que es √3, aproximadamente 1,7321 cm2), los círculos de Malfatti ocupan un área de aproximadamente 1,2629 cm2, mientras que los círculos de la distribución de Lob y Richmond tienen un área de aproximadamente 1,28 cm².
La situación es más evidente aún para un triángulo isósceles muy alto, es decir, con los lados iguales mucho mayores que el desigual. Una disposición de los círculos como aparecen en la segunda imagen, es decir, los tres seguidos y tangentes a los dos lados iguales del triángulo isósceles, tiene una superficie mucho mayor que la correspondiente a tres círculos de Malfatti.
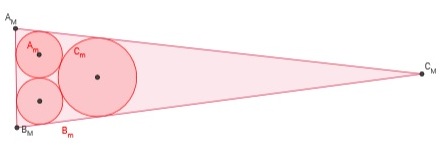
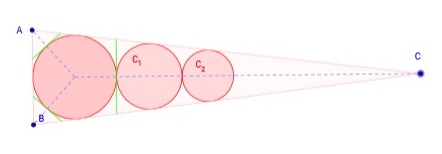
Michael Goldberg, en su artículo de 1967, demostró que una construcción del tipo de Lob-Richmond realizada para cualquier tipo de triángulo, siempre es de mayor área que la de los círculos de Malfatti, en consecuencia, estos nunca son una solución óptima al problema original de Gian Francesco Malfatti.
El problema original de Malfatti quedó completamente resuelto en 1994, cuando V. A. Zalgaller y G. A. Los, en su artículo The solution of Malfatti’s problem, clasificaron todas las formas de obtener tres círculos de máxima superficie dentro de un triángulo.
En concreto, Zalgaller y Los demuestran que existen 14 formas disposiciones rígidas de tres círculos (las disposiciones rígidas son aquellas que dejando fijos dos de los círculos, el tercero no se puede desplazar incrementando su radio), que no se superponen, sobre un triángulo. Las que aparecen en la siguiente imagen.
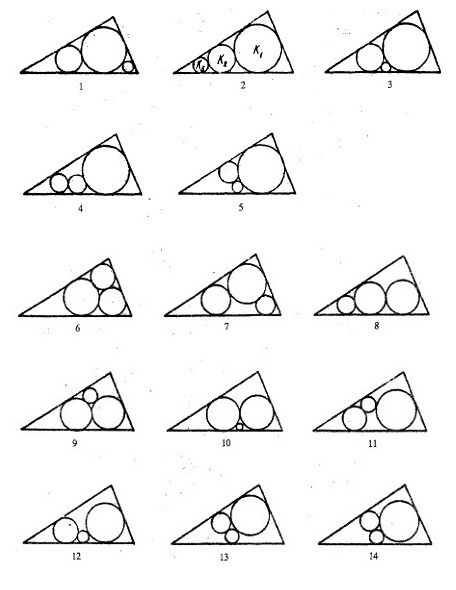
Además, en el artículo The solution of Malfatti’s problem se analiza, disposición a disposición, la posibilidad de ser maximal respecto al área, es decir, sean una solución al problema original de Mafatti, y se demuestra que las disposiciones 3-14 nunca pueden ser maximales, e incluso se obtienen condiciones para saber cuando son maximales las disposición 1 o la disposición 2.
Bibliografía
1.- George E. Martin, Geometric constructions, Springer-Verlag, 1998.
2.- Marco Andreatta, András Bezdek, Jan Boronski, The problem of Malfatti: Two centuries of debate, Mathematical Intelligencer 33, n. 1 (2010), 72–76.
3.- Gian Francesco Malfatti, Memoria sopra un problema stereotomico, Memoria di Matematica e Fisica della Società Italiana delle Scienze, X (1803), 235-244.
4.- Mirolad Stepanovic Triangle centers associated with the Malfatti circles, Forum Geometricorum 3 (2003), 83-93.
5.- Wikipedia: Malfatti circles [https://en.wikipedia.org/wiki/Malfatti_circles]
6.- J. Steiner, Gesammelte Werke, 2 volumes, edited by K. Weierstrass, 1881.
7.- Heinrich Dorrie, 100 Great Problems of Elementary Mathematics: Their History and Solutions, Dover, 1965.
8.- Geogebra: Malfatti’s problem- Steiner solution [https://www.geogebra.org/m/GDOLfx5y]
9.- H. Lob, H. W. Richmond, The solution of Malfatti’s problem for a triangle, Proc. London Math. Soc. 30 (1930), 287-304.
10.- Michael Goldberg, On the original Malfatti problem, Mathematics Magazine 40 (1967), 241-247.
11.- 8.- Geogebra: Malfatti’s packing problem [https://www.geogebra.org/m/bXjAVqhf]
12.- V. A. Zalgaller, G. A. Los, The solution of Malfatti’s problem, Journal of Mathematical Sciences, vol. 72, n. 4 (1994), 3163-3177.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica