En la anterior entrada del Cuaderno de Cultura Científica titulada Las curiosas reglas de divisibilidad presentamos algunos criterios de divisibilidad de los números de un solo dígito, es decir, de las cifras básicas -no nulas- de nuestro sistema de numeración, y de algún número más, como 11, 12, 13 o 15.

En esta entrada vamos a seguir analizando las reglas de divisibilidad de la aritmética. Algunos son nuevos criterios para números ya vistos, como 7, 8 u 11, mientras que otros serán de números nuevos, como el 17. Además, muchos de estos criterios, incluidos algunos de los vistos en la entrada anterior, emanan de una idea general de la divisibilidad, el criterio de Pascal.

Reglas de divisibilidad del número 7. En la anterior entrada ya vimos un criterio para el número 7, que la suma alternada de los grupos de tres dígitos del número, empezando por la derecha, también sea divisible por 7. Por ejemplo, sabemos que el número 417.885.713 es divisible por 7 porque 713 – 885 + 417 = 245 también lo es, 245 = 7 x 35.

Pero existen más reglas de divisibilidad para este número. Los primeros criterios que vamos a mostrar son bastante sencillos de aplicar, si se hace de forma recursiva. La primera regla dice:

Un número es divisible por 7 si, y sólo si, la resta de dos veces el dígito de las unidades del resto de los dígitos del número es divisible por 7.

Por ejemplo, si tomamos el número 539, como 53 – 2 x 9 = 35, entonces es divisible por 7, mientras que 713 no lo es, ya que 71 – 2 x 3 = 65. Y para números grandes se puede utilizar de forma recursiva, así el número 4.357 será divisible por 7 si lo es 435 – 2 x 7 = 421, pero este lo será si 42 – 2 x 1 = 40 lo es. Pero 40 no es divisible por 7, luego tampoco 421, ni 4.357. Para números con muchos dígitos puede ser un criterio un poco largo, aunque efectivo.

El motivo por el que funciona este criterio es que el 21 es divisible por 7. Dado un número N, este puede escribirse de la forma N = 10 a + b, donde b son las unidades, y si fuese múltiplo de 7 se podría expresar de la forma 7k. Por lo tanto, si le restamos la cantidad 21b, entonces se obtiene que 10a – 20b = 7k – 21b, es decir, la igualdad

10 (a – 2b) = 7 (k – 3b),

de donde sale el criterio, ya que N es divisible por 7 si, y sólo si, a – 2b lo es.

Un razonamiento similar, pero utilizando que 49 es divisible por 7, nos permite obtener otro criterio muy parecido:

Un número es divisible por 7 si, y sólo si, la suma de cinco veces el dígito de las unidades y el resto de los dígitos del número también lo es.

Es decir, si escribimos el número como 10 a + b, este es divisible por 7 si, y sólo si, a + 5b lo es. Por ejemplo, tomemos el número 3.791, este será divisible por 7 si lo es 379 + 5 x 1 = 384, que a su vez es divisible por 7 si lo es 38 – 5 x 4 = 18, que como no lo es, en consecuencia, no lo es ninguno de los anteriores, ni 384, ni 3.791.

Y el mismo tipo de argumento nos lleva, por ejemplo, a obtener el siguiente criterio:

Un número es divisible por 7 si, y sólo si, la suma del dígito de las unidades y tres veces el resto de los dígitos del número es divisible por 7.

Es decir, si escribimos el número como 10 a + b, este es divisible por 7 si, y sólo si, 3a + b lo es. Curiosamente, en el Talmud, que como señala el diccionario de la RAE es el “libro que contiene la tradición oral, doctrinas, ceremonias y preceptos de la religión judía”, está escrito otro criterio similar a los anteriores, basado en el hecho de que 98 es divisible por 7, que dice que 100 a + b es divisible por 7 si, y sólo si, 2a + b lo es.

Un reto sencillo para las personas que estáis leyendo esta entrada del Cuaderno de Cultura Científica consiste en probar estas tres últimas reglas de divisibilidad, de forma paralela a como hemos hecho para la primera.

Para la siguiente regla de divisibilidad se necesitan los restos de dividir por 7 las potencias de 10, asociadas a la representación decimal de los números. Como 10⁰ = 1, 10¹ = 7 + 3, 10² = 7 x 14 + 2, 10³ = 7 x 142 + 6, 10⁴ = 7 x 1.428 + 4 y 10⁵ = 7 x 14.285 + 5, los restos de dividir las anteriores potencias de 10 por 7 son 1, 3, 2, 6, 4, 5 y para las siguientes potencias de 10 los restos se repiten de forma cíclica 1, 3, 2, 6, 4 y 5.

El criterio dice lo siguiente:

Un número es divisible por 7 si, y sólo si, al multiplicar los dígitos del número por el resto correspondiente a la potencia de 10 de su posición, el resultado es divisible por 7.

Veamos el criterio mediante un ejemplo concreto. El número 234.647 será divisible por 7 si lo es 2 x 5 + 3 x 4 + 4 x 6 + 6 x 2 + 4 x 3 + 2 x 1 = 77, luego sí lo es (77 = 7 x 11).

Veamos la justificación de esta regla de divisibilidad del 7 para números de seis dígitos, aunque realmente funciona para cualquier cantidad de dígitos. Sea un número de seis dígitos a₅a₄a₃a₂a₁a₀, entonces

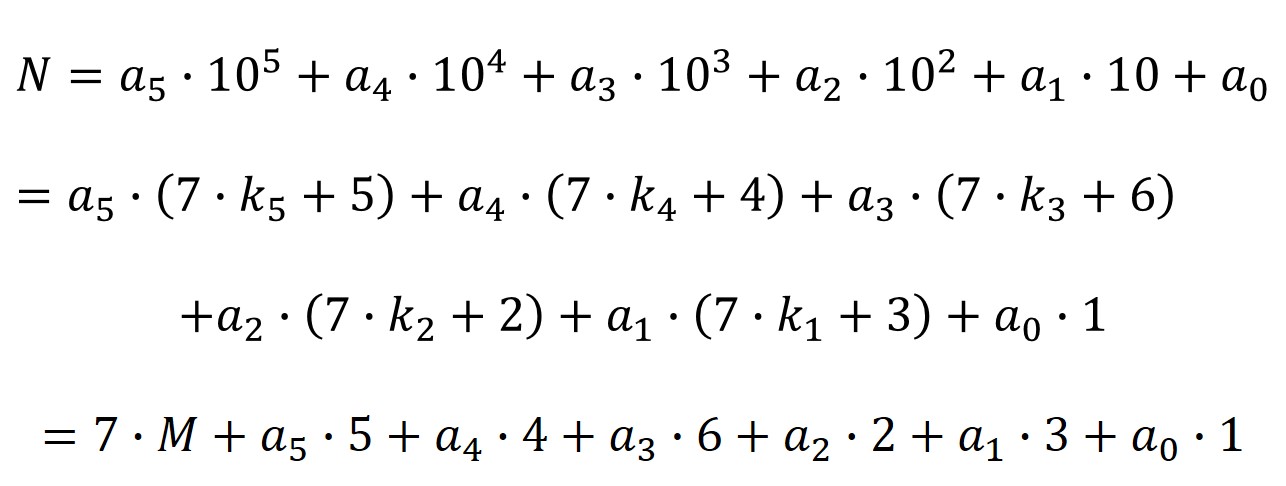
Por lo tanto, N es divisible por 7 si, y sólo si, (a₅ x 5) + (a₄ x 4) + (a₃ x 6) + (a₂ x 2) + (a₁ x 3) + (a₀ x 1) también es divisible por 7.

De hecho, podríamos ir un poco más allá para simplificar esta regla. Como 7 = 7 + 0, 8 = 7 + 1 y 9 = 7 + 2, podemos sustituir, a la hora de aplicar la regla al número, el 7 por 0, el 8 por 1 y el 9 por 2, en el número original. Así, para saber si el número 144.879, basta verlo para el número 144.102, así como 1 x 5 + 4 x 4 + 4 x 6 + 1 x 2 + 0 x 3 + 2 x 1 = 49, entonces sí es divisible por 7.

De hecho, este es solamente un caso particular del criterio de Pascal, que introdujo el matemático francés Blaise Pascal (1623-1662), de quien ya hablamos en la entrada Blaise Pascal, Dios y la cicloide, en su libro De Numeris Multiplicibus. El criterio de Pascal es el siguiente.

Criterio de Pascal: Un número N = a_n a_n–1 … a₂ a₁ a₀, es decir,

es divisible por un número m si, y sólo si, el número

es divisible por m, donde r_k es resto de dividir 10^k por m (r₀ = 1).

La demostración del criterio de Pascal es similar a la explicación que hemos dado para la última regla de divisibilidad del 7.

Muchas de las reglas vistas en la entrada Las curiosas reglas de divisibilidad son realmente consecuencia del criterio de Pascal. Por ejemplo, si miramos de nuevo a la regla de divisibilidad del 3, realmente se utiliza que el resto de dividir las potencias de 10 por 3 es siempre 1, por eso sale que la suma de los dígitos del número debe ser divisible por 3.

A continuación, vamos a mostrar un pequeño truco de magia que el divulgador estadounidense Martin Gardner (1914-2010) nos enseñó en su columna de juegos matemáticos en la revista Scientific American. Aunque no es una aplicación de las reglas de la divisibilidad, si tiene que ver con la divisibilidad. En concreto, está relacionado con el hecho, visto en la anterior entrada, de que 1.001 = 7 x 11 x 13.

El truco conocido como El misterio de las mil y una noches consiste en lo siguiente. Se le pide a una persona de nuestro “público” que piense en un número de tres cifras –ABC– y que lo escriba en una calculadora, que tendremos preparada para el truco. Después se le pide que vuelva a escribir, seguido, el mismo número, quedando entonces en la calculadora ABCABC. Nosotros no debemos saber el número y lo mejor es que estemos de espalda al “público” para que no haya sospechas.

Luego llega el momento de adivinar el número que ha pensado esa persona y hay que hacerlo con teatralidad. Puede empezar diciéndose algo así como “esperad que me concentre en el número que está escrito en la calculadora, estoy captando algo, sí creo que sí, … si no me equivoco es divisible por el número de la mala suerte, el 13”. Le pedimos que lo compruebe, que divida el número que está en la calculadora –ABCABC– por 13. Y se le pregunta, “¿Es cierto? ¿Era divisible por 13?” y cuando nos diga que sí, volvemos al teatro de mentalista.

Se puede seguir diciendo algo así como “sigo teniendo una sensación extraña, me parece que … sí, también creo que es divisible por el número de la buena suerte, el 7. ¿Estaré equivocado? ¿Divide el número que tienes en la calculadora por 7?¿Se ha podido dividir?”. Realizará la división –el resultado de dividir ABCABC por 13, lo divide ahora por 7– y contestará que sí.

Llega entonces el momento final del truco. El mago debe seguir ejerciendo de mentalista y decir algo así como “Percibo más cosas… percibo un uno, qué raro … espera … no, son dos unos, es el número 11 … divide el número que te ha quedado por 11”. Cuando la persona del “público” realice esa división, llega el efecto final… “fíjate bien en la pantalla de la calculadora, ¿no es ese el número que habías pensado?” y efectivamente, ahí está el número que había pensado, ABC.

El truco es muy sencillo y funciona porque ABCABC = 1.001 x ABC, pero 1.001 = 7 x 11 x 13.

Las reglas de divisibilidad del 8. Con el número 8 también podemos dar criterios de los dos tipos que hemos mostrado para el número 7, además del que mostramos ya en la anterior entrada. Un criterio de la primera clase es:

Un número 10 a + b es divisible por 8 si, y sólo si, 2a + b es divisible por 8.

Veamos un ejemplo. El número 5.176 será divisible por 8 si lo es 2 x 517 + 6 = 1.040, que a su vez es divisible por 8 si lo es 2 x 104 + 0 = 208, que claramente es divisible por 8, aunque podríamos volver a usar el criterio, ya que 2 x 20 + 8 = 48, divisible por 8.

Si ahora adaptamos el criterio de Pascal al número 8, necesitamos los restos de dividir las potencias de 10 por 8, que son 1, 2, 4 y el resto 0, ya que 1.000 y las potencias mayores son todas múltiplos de 8 (pensemos que cada 10 aporta un 2). Por lo tanto, el criterio de Pascal para el 8 queda:

Un número es divisible por 8 si, y sólo si, el resultado de sumar el dígito de las unidades, dos veces el de las decenas y cuatro veces el de las centenas es divisible por 8.

Veámoslo con el número anterior, 5.176, para el que 6 + 2 x 7 + 4 x 1 = 24, divisible por 8, como ya sabíamos.

Las reglas de divisibilidad del 11. El criterio visto en la anterior entrada, la suma alternada de sus dígitos (es decir, se va alternando suma y resta) es divisible por 11, no es el criterio de Pascal, pero está muy cerca, puesto que como demostramos entonces las potencias de 10 son casi múltiplos de 11, un número arriba o debajo de un múltiplo de 11.

Como 11 es mayor que 10, podemos aplicar la misma idea del criterio de Pascal, pero para la expresión del número como potencias de 100 y tomar los restos de dividir estas potencias por 11 (aunque también nos valdría para otros números de dos dígitos). Por ejemplo, el número 979.957 lo podemos expresar de la forma 97 x 100² + 99 x 100 + 57. De esta forma, se puede demostrar un nuevo criterio de tipo Pascal:

Criterio de tipo Pascal: Un número N = a_n a_n–1 … a₂ a₁ a₀(con una cantidad par de dígitos, en caso contrario es como si tuviese el dígito 0 a la izquierda, para que sea par), es decir,

es divisible por un número m si, y sólo si, el número

es divisible por m, donde r_k es resto de dividir 10^2k por m (r₀ = 1).

Como el resto de dividir las potencias de 100 por 11 siempre es 1, la regla de divisibilidad que se genera es:

Un número es divisible por 11 si, y sólo si, también lo es el resultado de sumar los grupos de dos dígitos (desde la derecha) del número.

Por ejemplo, 3.719 no es divisible por 11 ya que 37 + 19 = 56 no lo es. Sin embargo, el número anterior, 979.957, sí lo es ya que 97 + 99 + 57 = 253 es divisible por 11, para lo cual volvemos a utilizar el criterio, 53 + 2 = 55, múltiplo de 11.

O podemos dar algún criterio del otro tipo, como:

Un número 10 a + b es divisible por 11 si, y sólo si, a – b es divisible por 11.

Antes de ver más criterios, incluyamos uno de esos problemas de ingenio que tanto nos gustan, relacionado con este tema.

Problema: Encontrar el número capicúa más pequeño que es divisible por 3, 5 y 11.

Os animo a que lo resolváis por vosotros mismos, ya que es sencillo y lo divertido con los juegos es intentarlo uno mismo. De todas formas, damos a continuación la solución al mismo.

Como se trata de un número divisible por 5, debe terminar en 0 o 5, pero como no hay números que empiecen por 0 (a la izquierda), necesariamente el primer y último dígitos debe ser 5. Solo hay uno con dos dígitos –55–, pero no es divisible por 3. De tres dígitos que sean múltiplos de 3, por la regla de divisibilidad del 3, están 525, 555, 585, pero ninguno es múltiplo de 11, ya que la suma alternada de sus dígitos –8, 5 y 2, respectivamente– no es en ningún caso múltiplo de 11. Cualquier número capicúa de cuatro dígitos es divisible por 11 (en general, todos los números capicúas con una cantidad par de dígitos, como vimos en la entrada Las curiosas reglas de divisibilidad, son divisibles por 11), luego solo hay que buscar el número más pequeño de la forma 5aa5, divisible por 3, es decir, 5.115.

Las reglas de divisibilidad del 13. La regla de divisibilidad del 13 vista en la anterior entrada del Cuaderno de Cultura Científica es la misma que para 7 y 11, que la suma alternada de los grupos de tres dígitos del número, empezando por la derecha, también sea divisible por 13. Pero podemos dar algunos criterios similares a los del primer tipo estudiados para el 7.

Criterio 1: Un número 10 a + b es divisible por 13 si, y sólo si, a + 4b es divisible por 13.

Criterio 2: Un número 100 a + b es divisible por 13 si, y sólo si, 4a – b es divisible por 13.

Criterio 3: Un número 10 a + b es divisible por 13 si, y sólo si, a – 9b es divisible por 13.

Veamos la divisibilidad por 13 del número 8.333. Por el criterio 1 sería divisible si lo es 833 + 4 x 3 = 845, que a su vez lo será si lo es 84 + 4 x 5 = 104, que es divisible por 13 ya que 10 + 4 x 4 = 26.

Aplicando el criterio 2, 8.333 es divisible por 13 si lo es 4 x 83 – 33 = 299, que es múltiplo de 13, puesto que 4 x 2 – 99 = 91, que es siete veces 13.

Y mediante el criterio 3, tenemos 833 – 9 x 3 = 806 y a partir de este, 80 – 9 x 6 = 26.

Las reglas de divisibilidad del 17. Para este número se pueden encontrar, de nuevo, varios criterios de divisibilidad del primer tipo, aunque vamos a citar solamente uno.

Un número 10 a + b es divisible por 17 si, y sólo si, a – 5b es divisible por 17.

Por ejemplo, el número 289 es divisible por 17 ya que 28 – 5 x 9 = – 17, lo es.

Como hicimos para el número 11 podemos intentar aplicar el criterio de tipo Pascal anterior para el número 17. Para lo cual necesitamos conocer los restos de dividir las potencias de 100 por 17, que son (además del resto inicial 1) los siguientes: el resto de dividir 100 por 17 es 15, pero como es muy grande y nos interesa los múltiplos de 17, podemos restarle 17, quedando – 2; el resto para 100² es 4; el resto para 100³ es 9; el resto para 100⁴ es 16, que restándole 17 queda – 1; el resto para 100⁵ es 2; y así podríamos seguir.

Veamos un ejemplo de aplicación de este criterio de tipo Pascal para el número 17. Tomemos el número 333.333.331 (más adelante entenderemos el motivo de elegir este), será divisible por 17 si lo es

3 x (– 1) + 33 x 9 + 33 x 4 + 33 x (– 2) + 31 x 1 = 391,

que es múltiplo de 17 (al multiplicarlo por 23), aunque podemos utilizar una vez más el criterio, por lo que 391 es múltiplo de 17 si lo es

3 x (– 2) + 91 x 1 = 85,

que es 17 x 5. Por lo tanto, el número 333.333.331 se puede dividir por 17.

Veamos una cuestión sobre patrones de números primos que se puede leer en el libro de Martin Gardner, Huevos, nudos y otras mistificaciones matemáticas.

Si se observa la sucesión de números 31, 331, 3.331, 33.331, 333.331, 3.333.331, 33.333.331… se verá que esos primeros miembros son todos números primos, la cuestión es si toda la sucesión será de números primos y en caso contrario, cuál es el primero que no lo es.

Las reglas de la divisibilidad no son la mejor herramienta para resolver este problema, ya que con una calculadora podemos hacer rápidamente algunas cuentas y observar la solución. Además, ya hemos probado más arriba que el siguiente miembro de la sucesión 333.333.331 es divisible por 17, luego no primo. De hecho,

333.333.331 = 17 x 19.607.843.

Sin embargo, podemos utilizar las reglas de la divisibilidad para obtener algunas conclusiones generales sobre esta sucesión de números, 31, 331, 3.331, etc.

Claramente, los miembros de esa sucesión no son múltiplos de 2 o 5, ya que el dígito de las unidades es 1. Tampoco ningún miembro es múltiplo de 3, ya que la suma de sus dígitos es de la forma 3 k + 1, donde k es el número de treses que tiene el número, luego nunca puede ser múltiplo de 3.

Veamos qué pasa con el siguiente primo, el 7. Si utilizamos el criterio de que un número 10 a + b es divisible por 7 si, y sólo si, lo es a – 2b, se observa que, para cada miembro de la sucesión, al aplicar el criterio se genera el miembro anterior. Por ejemplo, dado 3.331, este sería divisible por 7 si lo fuese 333 – 2 x 1 = 331, que es el elemento anterior. Por lo tanto, como los primeros miembros de la sucesión son primos, ningún elemento de esta sucesión es múltiplo de 7.

Si utilizamos la regla de divisibilidad del 11 de las sumas alternadas, observaremos que las sumas alternadas de los miembros de la sucesión 31, 331, 3.331, 33.3331, … son siempre 2 y 1, repitiéndose de forma cíclica, luego nunca múltiplos de 11. De la misma forma, si se utiliza el criterio de divisibilidad del 13 de las sumas alternadas de los grupos de tres dígitos, se obtienen siempre las sumas – 328, – 298, 2, 1, 31 y 331, repitiéndose de forma cíclica, luego tampoco son múltiplos de 13.

Resumiendo, con estos criterios de divisibilidad, hemos probado que los miembros de la sucesión infinita

31, 331, 3.331, 33.331, 333.331, …

no son divisibles por los números primos 2, 3, 5, 7, 11 y 13.

Podríamos dar reglas de divisibilidad para más números, pero “creo que lo dejaré aquí” (véase la entrada Euler y el último teorema de Fermat, para ver donde esta última expresión tuvo un sentido muy especial).

Bibliografía

1.- Martin Gardner, The Unexpected Hanging and other Mathematical Diversions, University of Chicago Press, 1991.

2.- Branislav Kisacanin, Mathematical Probems and Proofs, Kluwer, 2002.

3.- Wikipedia: Divisibility rule

4.- James J. Tattersall, Elementary Number Theory in Nine Chapters, Cambridge University Press, 1999.

5.- Página web del artista Tobia Ravá

6.- Página web del artista Andreas Kopp

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica