De nuevo, una entrega de la sección Matemoción del Cuaderno de Cultura Científica está inspirada por uno de los maravillosos libros de la editorial puntodepapel , cuyo lema, volvemos a recordar, es “aprender no es un juego, pero jugando se aprende”. El libro que nos sirve de musa en esta entrega es “Buscando a LO”, de la artista murciana Teresa Navarro, autora de libros tan fascinantes como “La rebelión de las formas” (2010) o “Concertina y el dragón” (2012). Al igual que en otros de sus libros, como los recientes “Paulhexaedro”, “Theresio” o “Fantasmilla”, en él se entremezclan las matemáticas, la literatura y el arte.

La conocida sucesión de Fibonacci (1, 1, 2, 3, 5, 8, 13,…) y su relación con la naturaleza son los protagonistas de este encantador cuento. No es la primera vez que Teresa Navarro incluye esta sucesión en uno de sus libros. Ya aparecía en “Concertina y el dragón”, aunque en esa ocasión en relación con la música. Cuando uno despliega en su totalidad la publicación “Buscando a LO” descubre una bella pintura del nautilus y la espiral que forma su concha. Esta imagen me ha animado a escribir en esta entrada del Cuaderno de Cultura Científica sobre la sucesión de Fibonacci y su presencia en la cultura.

1. Fibonacci

Para empezar, recordemos cual es la sucesión de Fibonacci y su origen. Esta sucesión infinita de números aparece asociada al famoso problema de los conejos que Leonardo de Pisa (1170-1241), conocido como Fibonacci, plantea (entre otros problemas) en su libro “Liber Abaci” (1202, El libro del Ábaco). El problema es el siguiente:

“Consideremos una familia de conejos con la característica de que tardan un mes en ser fértiles. Cuando han alcanzado la fertilidad, cada pareja se aparea teniendo al mes siguiente (cada hembra) una pareja de crías (un macho y una hembra) que de nuevo tardarán en ser fértiles un mes y entonces se aparearán. Así, según va transcurriendo el tiempo, irá aumentando el número de parejas de conejos. Fibonacci preguntó cuántas parejas de conejos habría al cabo de un tiempo dado.”

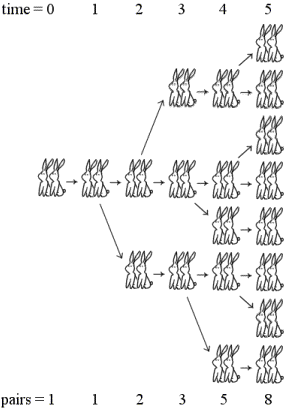
No es difícil darse cuenta de que la sucesión del número de parejas de conejos que hay cada mes

1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 …

tiene la propiedad de que cada término de la sucesión es la suma de los dos términos anteriores. La razón es sencilla, y se ve claramente si realizamos un esquema por meses, ya que cada mes estarán las parejas del mes anterior más las nuevas parejas que serán las crías de las parejas fértiles en ese momento, es decir, las que estaban dos meses antes. Esta sucesión aparece bajo la denominación A000045 dentro de “La enciclopedia on-line de las sucesiones de números enteros” (con siglas en inglés, OEIS).

Aunque pueda sorprender, los números de Fibonacci están muy presentes en botánica, y más concretamente en la filotaxis, una parte de la morfología vegetal que se dedica al estudio de la composición, ordenación y disposición de las hojas (filos) a lo largo de los tallos, así como de los brotes o las semillas. Por ejemplo, en las espirales de los girasoles y piñas, o en la disposición helicoidal de las hojas en el tallo, pero de ese tema hablaremos en otra ocasión. En la presente entrada vamos a mostrar algunos ejemplos de la presencia de esta sucesión en la cultura.

2. Literatura

La sucesión de Fibonacci aparece, por ejemplo, en el bestseller mundial “El código da Vinci” (Umbriel, 2004) de Dan Brown. Aparece en varias ocasiones a lo largo de la novela. Al principio de la novela, en la escena del crimen del conservador del Museo del Louvre, Jacques Saunière, aparecen pintados en el suelo de la galería los números 13-3-2-21-1-1-8-5. Como se ve son los ocho primeros números de Fibonacci, pero desordenados.

“Langdon no lograba apartar la vista de aquellas letras que brillaban sobre el suelo de madera. Le parecía totalmente inverosímil que aquellas fueran las últimas palabras de Jacques Saunière.

El mensaje rezaba así:

13-3-2-21-1-1-8-5

¡Diavole in Dracon!

Límala, asno

Aunque Langdon no tenía ni la más remota idea de qué significaba aquello, ahora entendía que, intuitivamente, Fache hubiera relacionado el pentáculo con el culto al diablo.

“¡Diavole in Dracon!”

Saunière había dejado escrita una referencia literal a diablesas. Igualmente rara era la serie numérica.

— Una parte al menos parece un mensaje cifrado.

— Sí –respondió Faché–. Nuestros criptógrafos ya están trabajando en ello. Creemos que tal vez los números contengan la clave que nos diga quien le mató. Puede que nos lleven a un teléfono o a algún tipo de identificación fiscal. ¿Tienen para usted algún tipo de significado simbólico?”

Posteriormente estos dígitos ordenados se convertirán en el número de cuenta que da acceso a una caja de depósitos de un banco. Además, en cierto momento, explican que la sucesión de Fibonacci está relacionado con el número de oro, divina proporción, así como su relación con el arte y la naturaleza.

Veamos una presencia menor de los números de Fibonacci en la literatura. Normalmente los capítulos de un libro, y en particular, en una novela, suelen nombrarse con los números naturales, es decir, 1, 2, 3, 4, 5, 6, etc correspondiéndose el orden natural de los números con el orden de la lectura. Sin embargo, existen algunas novelas en las cuales se han cambiado estos números naturales por alguna otra sucesión de números que nos permiten nombrar los capítulos de la novela con un poquito más de gracia e imaginación.

En el libro “El curioso incidente del perro a medianoche” (Mark Haddon, Salamandra, 2004) se utilizan los números primos, desde el 2 hasta el 229, mientras que en el libro “La conjetura de Perelman” (Soto Ivars, Ediciones B, 2011) se empiezan a nombrar los capítulos con el número 14, después 13, y así en sentido descendente hasta el 1, en la primera parte de la novela, mientras que en la segunda parte, se empieza en 1, luego el 2, y se termina en el capítulo 14. En el libro “Crónicas de la última revolución” (Antoni Casas Ros, Seix Barral, 2012) se numeran los capítulos precisamente con los números de la sucesión de Fibonacci, desde 1 (solamente una vez) hasta 89.

3. Poesía

Algunos poetas han hecho uso de la sucesión de Fibonacci para definir la estructura de sus poemas. Así, la escritora danesa Inger Christensen (1935-2009) la utiliza en una de sus obras más conocida “Alfabet” (Alfabeto), de 1981. Esta poetisa trabaja con dos restricciones en su poema, el alfabeto, de la A hasta la N, y la sucesión de Fibonacci (1 2 3 5 8 13 21 34…610). Cada una de las estrofas de “Alfabet” se inicia con la correspondiente letra del alfabeto, desde la A de Albaricoque a la N de Noche, y de hecho esa letra está presente en toda la estrofa (véase en el trozo del poema que se muestra más abajo). Pero además, el número de versos de cada estrofa se corresponde con cada uno de los números de Fibonacci, así la primera estrofa, correspondiente a la letra A, tiene 1 verso, la segunda, relacionada con la letra B, tiene 2 versos, la estrofa de la letra C tiene 3 versos, 5 versos la de la letra D, y así hasta completar las 14 estrofas del poema.

1-A (1 verso)

apricot trees exist, apricot trees exist

(el albaricoquero existe, el albaricoquero existe)

2-B (2 versos)

bracken exists; and blackberries, blackberries;

bromine exists; and hydrogen, hydrogen

(el helecho existe; y las moras, las moras;

el bromo existe; y el hidrógeno, el hidrógeno)

3-C (3 versos)

cicadas exist; chicory, chromium,

citrus trees; cicadas exist

cicadas, cedars, cypresses, the cerebellum

(las cigarras existen; la achicoria, el cromo

los limoneros, las cigarras existen;

cigarras, cedros, cipreses, el cerebelo)

4-D (5 versos)

doves exist, dreamers, and dolls;

killers exist, and doves, and doves;

haze, dioxin, and days; days

exist, days and death; and poems

exist; poems, days, death

(las palomas existen, los soñadores, y las muñecas;

existen asesinos, y palomas, y las palomas;

niebla, la dioxina, y días, días

existen, los días y la muerte, y poemas

existen, poemas, los días, la muerte)

[…]

Al parecer, no es el único poeta que hace uso de los números de Fibonacci en sus poemas. Según se menciona en el libro “The Mathematics of Harmony. From Euclid to Contemporary Mathematics and Computer Science” (Alexey Stakhov, World Scientific, 2009), el poeta ruso Alexander Pushkin (1799-1837) tenía preferencia por los poemas que tuviesen 5, 8, 13, 21 y 34 versos, que son precisamente números de Fibonacci. Aprovechemos la mención para incluir aquí uno de sus poemas (y, por supuesto, que tenga el número de versos que se ajuste al comentario). El poema es “Apuro sediento tu tierno gemido…”, que he encontrado en la página Poetas Siglo XXI…

Apuro sediento tu tierno gemido,

tu intimidad que me embriaga

y ardiente, la lengua del dulce deseo,

pasión cuyo vino no sacia.

Pero corta con ese relato,

oculta, calla tu sueño:

su llama que quema yo temo,

tengo miedo de saber tu secreto.

4. Arte

En un par de ocasiones hemos podido ver en el Museo Guggenheim de Bilbao la obra “Crocodrilus Fibonacci” (1972) del artista italiano Mario Merz (1925-2003). Esta instalación consiste en un cocodrilo seguido por una sucesión de números en neón, exactamente los números de Fibonacci. Es muy probable que Merz esté jugando aquí con la misma idea de los conejos, pero trasladada a los cocodrilos.

El artista Mario Merz, perteneciente al movimiento Arte Povera (arte pobre en italiano) se ha hecho famoso por sus numerosas y variadas instalaciones con los números de fibonacci en neón. Le fascinaba la geometría de la naturaleza, y especialmente la sucesión de Fibonacci y las espirales, que también aparecen en varias de sus obras. Un ejemplo es una chimenea en Turku (Finlandia) en un proyecto artístico relacionado con el medio ambiente (1994), en la que encontramos la sucesión de Fibonacci hasta el número 55.

Otro ejemplo es “Sin Título (A real sum is a sum of people)” (1972), en el que vemos fotografías de una escena y entre foto y foto hay un número de fibonacci. Las fotografías tienen el mismo escenario, un café o restaurante, pero en cada foto hay tantas personas como indica el número de fibonacci en neón que acompaña la fotografía.

También incluye los números de Fibonacci en varios de sus famosos igloos, como “La casa de Pitágoras” (1994) o “Lugares sin calles” (1987). Y así podríamos hablar de una gran cantidad de instalaciones realizadas por Merz que hacen uso de estos números, como “Crescendo appare” (1992), que está en el Paseo Joan de Borbó de Barcelona.

Pero no es el único artista, ni mucho menos, que utiliza la sucesión de Fibonacci. Como por ejemplo la famosa serie de esculturas “Ratio” (proporción) realizadas por el escultor australiano de Land Art, Andrew Rogers (Israel, India, Sri Lanka,…). Está formada por bloques, con forma de prisma de cara cuadrada, dispuestos en columnas distribuidas de simétricamente de alturas iguales a un capicúa de Fibonacci, 1 1 2 3 5 8 5 3 2 1 1 (o llegando también a 13). Pero en esta obra como en otras muchas no aparecen los números explícitamente.

¿Hay más obras en las que aparezcan, de nuevo explícitamente, los números de la sucesión de fibonacci? Sí, por ejemplo, la artista austriaca Martina Schettina, que descubrí hace unos años, utiliza la sucesión de Fibonacci en varias de sus obras. Una de ellas es “El sueño de Fibonacci” (2008), de la serie Mathe 2008, donde observamos una serie de números distribuidos en aspa sobre un fondo gris. Los números son los pertenecientes a la citada sucesión, desde el 1 inicial que está en una esquina hasta en que está en el centro, 10.946.

O la pintura “Rojo anaranjado de Fibonacci” (2009), de la serie Mathe Color 2009. De los últimos en los que utiliza la sucesión de Fibonacci están los cuadros “Fibonacci I” y “Fibonacci II” de la serie Mathe Symposium 2009. Esta artista es una apasionada de las matemáticas, y en particular, de los números.

5. Música

Es bastante conocido que el compositor hungaro Béla Bartók (1881-1945) utilizó esta sucesión de números para desarrollar una escala musical que denominó “escala fibonacci”. Quien esté interesado en este tema puede leer el artículo de Iñigo Ibaibarriaga “Música y Matemáticas, de Schoenberg a Xenakis”. Ibaibarriaga también comenta que quizás uno de los primeros usos de la sucesión de Fibonacci en la música podría ser la quinta sinfonía de Beethoven, aunque podría no ser una utilización intencionada.

Sin embargo, a mi me gustaría traeros hoy una pieza más moderna. Una de mis estudiantes de la Licenciatura de Matemáticas, Zuriñe Aguirre, me recomendó que escuchara la canción “Lateralus” (que pertenece al disco del mismo nombre, de 2001) del grupo estadounidense de metal progresivo Tool, en la cual la sucesión de Fibonacci tenía un papel fundamental. En el siguiente video podéis escuchar la canción, así como ir leyendo la explicación de la presencia de la sucesión de Fibonacci. En particular, las silabas de cada estrofa siguen la sucesión de Fibonacci…

Black [1] then [1] white are [2] all I see [3] in my infancy [5] red and yellow then came to be [8] reaching out to me [5] lets me see [3] …

…as below so above and beyond I imagine [13] drawn beyond the lines of reason [8] push the envelope [5] watch it bend [3] …

6. Demostraciones sin palabras (matemáticas)

Vamos a concluir la entrada de hoy con una demostración visual (ya hemos hablado de demostraciones sin palabras en los artículos del Cuaderno de Cultura Científica, Pitágoras sin palabras, El teorema de la pizza, Regla de los números intermedios y el parque automovilístico de Bilbao o Formas ritmo-espacio) de una fórmula matemática relacionada con la suma de los cuadrados de los números de Fibonacci, y que aparece en el magnífico libro de Roger B. Nelsen “Demostraciones sin palabras” (Proyecto Sur, 2001).

La fórmula es la siguiente…

, para , donde denota el n-ésimo número de la sucesión de Fibonacci.

Y la demostración sin palabras de la fórmula de las sumas de cuadrados de números de Fibonacci (Alfred Brousseau):

Y para terminar un chiste que me enviaron hace un tiempo (¡gracias a la persona que me lo envió!): “1 de enero, 1 de febrero, 2 de marzo, 3 de abril, 5 de mayo, 8 de junio, 13 de… -¿¡Pero quién ha invitado a Fibonacci a los San Fermines!?”.

Bibliografía:

1.- Teresa Navarro, Buscando a LO, editorial puntodepapel, 2014.

2.- VVAA (coordinadores R. Ibáñez, Antonio Pérez Sanz), El Rostro Humano de las Matemáticas, Nivola, 2008.

3.- Ricardo Moreno, biografía de Fibonacci en divulgamat (biografías de matemáticos ilustres)

4. VV. AA., El rostro humano de las matemáticas, Nivola, 2008.

(puede verse la versión on line de la exposición –en euskera, castellano, catalán, gallego y valenciano en divulgamat)

5.- Antoni Casas Ros, Crónicas de la última revolución, Seix Barral (Biblioteca Formentor), 2012.

6.- Marta Macho, Inger Christensen (1935-2009), Espacio Luke, 103, 2009.

7.- El establo de Pegaso, Inger Christensen, 2011

8.- Página web de Martina Schettina,

9.- Iñigo Ibaibarriaga, Música y Matemáticas, de Schoenberg a Xenakis, Un paseo por la Geometría, UPV-EHU, 2004.

10.- Roger B. Nelsen, Demostraciones sin palabras (ejercicios de pensamiento visual), Proyecto Sur, 2001.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica