En mi anterior entrada del Cuaderno de Cultura Científica, El asesinato de Pitágoras, historia y matemáticas (I) [], comentamos los aspectos históricos de la novela “El asesinato de Pitágoras” (Duomo editorial, 2013), de Marcos Chicot. Pitágoras, Teano, Milón de Crotona, la hermandad de los Pitagóricos o la ciudad de Crotona en la Magna Grecia. El objetivo de la presente entrada es fijar nuestra atención en las matemáticas que aparecen citadas, en ocasiones de una forma superficial y en otras con mayor profundidad, en la mencionada obra literaria. El teorema de Pitágoras, la Tetraktys, las proporciones, los números irracionales, los poliedros regulares, el número pi, las raíces cuadradas, la sección áurea o el pentagrama pitagórico.

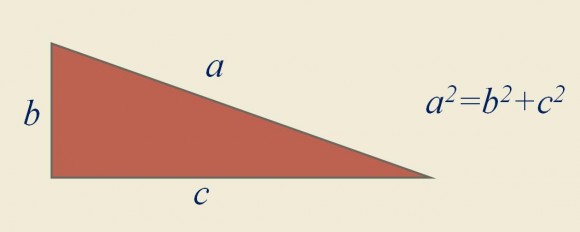
El teorema de Pitágoras. Si hay un resultado matemático que todo el mundo asocia con la figura del gran sabio y filósofo griego, ese es el teorema que lleva su nombre y que nos dice que dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos (la famosa expresión a² = b² + c², si c y b son los catetos y a la hipotenusa).

Y como no podía ser de otra forma, en esta novela, que centra su trama en torno a este matemático griego, dicho teorema tiene cierto protagonismo en relación con algunas de las cuestiones matemáticas que aparecen, como son el cálculo de los decimales del número pi o la existencia de las magnitudes inconmensurables (los números irracionales). El teorema de Pitágoras es también uno de los resultados matemáticos de los que más se ha escrito por eso no vamos a dedicarle mucho espacio en esta entrada, para aquellos que estéis interesados podéis leer mi entrada del cuadernoPitágoras sin palabras o el libro de Pedro Miguel G. Urbaneja, “Pitágoras, el filósofo del número”, libro que además es una referencia obligada para muchas de las cuestiones matemáticas que vamos a comentar aquí.

La Tetractys. Toda la filosofía pitagórica está basada en la importancia de los números, y como diría el pitagórico Filolao (aprox. 470-385 a.c.) “Todo lo cognoscible tiene un número, pues no es posible que sin número nada pueda ser concebido ni conocido”. En particular, los diez primeros números (que denominaban la década) tenían, por sus propiedades místicas y cabalísticas, una gran importancia para ellos. Así, por ejemplo, el número uno era la unidad, la mónada, generador de todos los números y dimensiones, símbolo de la razón, de la unidad, lo definido, lo estable, el lado derecho, era el demiurgo del mundo. Y de forma similar con el resto de los números.

El número diez era el más sagrado de todos los números y contenía a los anteriores, y además tantos pares como impares, tantos primos (1, 2, 3, 5, 7) como compuestos (4, 6, 8, 9, 10). Era el símbolo de Dios y del universo. El número diez es la suma de los cuatro primeros números (1 + 2 + 3 + 4 = 10), por lo que encerraba en sí mismo la esencia de la música (puesto que la escala pitagórica se podía generar a partir de los cuatro primeros números) o la suma de las dimensiones geométricas “posibles”. Los pitagóricos representaban el número 10 mediante diez piedras con una cierta distribución geométrica, formando un triángulo, que simbolizaba la suma de una, dos, tres y cuatro piedras (véase la imagen), y que recibía el nombre de tetractys.

La tetractys, junto al pentagrama místico, eran los dos símbolos más importantes de la hermandad. Uno de los juramentos del rito iniciático en la secta de los pitagóricos era el verso de oro “¡Lo juro por Aquel que ha dado a nuestro alma la tetractys, fuente y raíz de la naturaleza eterna!”.

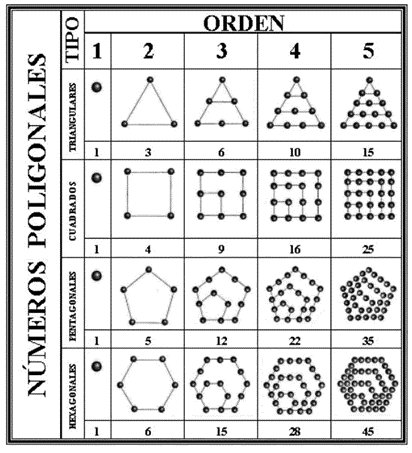
El símbolo de la tetractys estaba basado en el hecho de que el número 10 es un número triangular. Los pitagóricos estudiaron los números desde una perspectiva aritmético-geométrica, representándolos geométricamente. Así los números poligonales (triangulares, cuadrados, pentagonales, hexagonales,…) eran aquellos que se obtenían al representar el número como una disposición poligonal de puntos o piedras.

Los números triangulares, que como se muestra en la imagen anterior se obtienen al formar con las piedras, o puntos, un triángulo tal que en cada fila hay un elemento más que en la anterior, son el 1, 3, 6, 10, 15,…Observemos que cada número triangular nos da la suma de los primeros números naturales hasta un número dado, así el número triangular de orden 8 es 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36. Un sencillo ejemplo del razonamiento aritmético-geométrico con números poligonales sería la obtención de la fórmula de la suma de los n primeros números, que es un número triangular…

Las proporciones. Más allá de la importancia de la música en la forma de vida pitagórica, podemos decir que fue Pitágoras quien estudió por primera vez la relación entre los sonidos armónicos y los números, poniendo las bases de los fundamentos matemáticos de la armonía musical.

Se cuenta que se percató de esta correspondencia entre los números y la armonía musical al escuchar los sonidos producidos por martillos de diferentes tamaños utilizados por unos herreros. Y transformó esta experiencia en un experimento con cuerdas para descubrir que las longitudes de las mismas que proporcionan una nota, su cuarta, su quinta y su octava son proporcionales a los números 12, 9, 8 y 6, que son las mismas que hay entre los números 1, 3/4, 2/3 y 1/2, y por lo tanto, determinadas por los cuatro número iniciales relacionados con la Tetractys (1 +2 + 3 + 4 = 10).

Pero para Pitágoras no solamente “el número gobierna el tono musical” sino que va más allá y piensa que el número es la clave de toda la naturaleza y del cosmos, pensamiento recogido en el aforismo “el número es la esencia de todas las cosas”.

El concepto matemático que estaba detrás de esta idea de que todo se puede medir, que las magnitudes son conmensurables, es el de los “números racionales”, es decir, que cualquier magnitud –número- se podía expresar como la razón, o cociente, entre dos números naturales. O como lo expresaríamos hoy en día, solamente existirían los números racionales, aquellos que se pueden expresar como “p/q”.

Los números irracionales. Una crisis profunda del pensamiento pitagórico la marcó la existencia de los números inconmensurables. Este hecho se escondía detrás del teorema de Pitágoras, puesto que si se considera un triángulo rectángulo cuyos catetos valgan 1, la hipotenusa h (que por el teorema es tal que h² = 2) no es racional. Aunque autores como los filósofos griegos neoplatónicos Proclo (410-485) o Jámblico (aprox. 245-330) atribuyen al propio Pitágoras el descubrimiento de los inconmensurables, se suele conceder su autoría a Hipasos de Metaponto (siglo V a.c.), hacia el año 480 a.c., de quien se dice que murió asesinado por los pitagóricos por difundir ese resultado fuera de la hermandad.

En una nota (atribuida a Proclo) a “Los Elementos” de Euclides se dice…

Es fama que el primero en dar al dominio público la teoría de los irracionales pereciera en un naufragio, y ello porque lo inexpresable e inimaginable debería siempre haber permanecido oculto. En consecuencia, el culpable, que fortuitamente tocó y reveló este aspecto de las cosas vivientes, fue trasladado a su lugar de origen, donde es flagelado a perpetuidad por las olas

Marcos Chicot en la novela “El asesinato de Pitágoras” se permitiría una pequeña licencia histórica al atribuir al asesino de la novela la demostración de la existencia de inconmensurables en el año 510 a.c., año en que tienen lugar los hechos de la misma.

La proposición X.117 de “Los Elementos” (texto apócrifo añadido como complemento explicativo posterior y que aparece solo en algunas ediciones) recoge la demostración aristotélica, por reducción al absurdo, de que la raíz de 2 (la hipotenusa del triángulo rectángulo de catetos con medida 1) es irracional. La demostración es la siguiente…

Supongamos que la hipotenusa puede expresarse como el cociente p/q (siendo esta una fracción irreducible, con p y q sin factores comunes), es decir, (p/q)² = 2, o equivalentemente que p² = 2 q²; esto nos dice que p necesariamente es un número par, que puede expresarse como p = 2n, luego 2 q² = p² = (2n)² = 4 n², por tanto, q² = 2 n², y q sería también par, lo cual no puede ser posible por ser p/q una fracción irreducible.

Los poliedros regulares. En el diálogo “Timeo” Platón (427 a.c.-347 a.c.) relaciona los cuatro elementos naturales (fuego, tierra, aire y fuego) con los cuatro poliedros regulares (tetraedro, cubo, octaedro e icosaedro), y el dodecaedro con el cosmos. Aunque autores, como Proclo o el filósofo griego Aecio (siglo I o II a.c.), atribuyen esta cosmogonía a los pitagóricos, la mayoría de los investigadores consideran esto poco probable y asocian a la hermandad únicamente el conocimiento del tetraedro, el cubo y el dodecaedro, mientras que sería el matemático griego Teeteto (aprox. 417 a.c.-369 a.c.) quien estudió en profundidad los poliedros regulares.

En el libro XIII de “Los Elementos” de Euclides (aprox. 325-265 a.c.) se recoge el estudio sistemático de los poliedros regulares, conocidos como sólidos platónicos, debido a Teeteto. Así se demuestra la existencia de únicamente cinco poliedros regulares o se calculan los radios de las esferas en las que se inscriben estos.

Veamos la demostración de que existen exactamente cinco sólidos platónicos. Por una parte, todas las caras de los poliedros regulares son el mismo polígono regular y era ya conocido que el ángulo interior de un polígono regular de n lados mide (resultado que se atribuye al propio Pitágoras). Y por otra parte, en cada vértice de un poliedro regular hay siempre el mismo número de caras (polígonos regulares de n lados), que denotaremos m, entonces la suma de los ángulos que concurren en un vértice es

que tendra que ser menor que 360º. De donde se deduce fácilmente que , y las únicas soluciones posibles para m y n son:

a) si m = 3, entonces puede ser n = 3 (que es el caso del tetraedro, 3 triángulos en cada vértice), n = 4 (que es el cubo, con tres cuadrados en cada vértice) o n = 5 (el dodecaedro, con tres pentágonos en cada vértice);

b) si m = 4, entonces solo puede ser n = 3 (el octaedro, con cuatro triángulos en cada vértice);

c) y si m = 5, entonces n = 3 (el icosaedro, cinco triángulos en cada vértice).

Aunque los Pitagóricos ya conocían la inscripción del dodecaedro en una esfera, resultado de una gran relevancia, y le daban una importancia mística a este poliedro regular, quizás por su relación con el pentágono, asociándolo con el cosmos. De ahí esa parte de la cosmogonía de Platón. Jámblico escribe…

Se dice que primero que reveló la naturaleza de la conmensurabilidad e inconmensurabilidad a los indignos de participar de tales conocimientos fue aborrecido [por la comunidad pitagórica] hasta el punto de que no sólo lo expulsaron de la vida y de la vivienda en común, sino que incluso le erigieron una tumba como si él, que había sido una vez compañero, hubiese abandonado la vida entre los hombres. […] Otros afirman que la divinidad se enojó contra quien divulgó la doctrina de Pitágoras, pereciendo como un impío en el mar por sacrílego al haber revelado la doctrina de los números irracionales y la inconmensurabilidad.

El número pi. En la novela “El asesinato de Pitágoras” el sibarita Glauco convoca un premio que consiste en que la persona que sea capaz de calcular con exactitud al menos 4 decimales del número recibirá diez veces el peso de Glauco en oro (el investigador Akenón hace la cuenta y le sale que eso son unos mil quinientos kilos de oro), y lo hace para desafiar a Pitágoras, quien solamente conoce con exactitud el primer decimal, que es un 1, de . El asesino de la novela gana el premio haciendo uso del teorema de Pitágoras en un método de duplicación de polígonos, lo que le permite calcular hasta 8 decimales del número .

Por supuesto, esto es una licencia histórica de Marcos Chicot sobre el número , la razón entre el perímetro de un círculo y su diámetro. Los babilonios (hacia el 2.000 a.c.) habían llegado a una aproximación de igual a 3+1/8 = 3,125, mientras que los egipcios utilizaban 4 (8/9)² = 256/81 que es aproximadamente 3,1605. El primer avance significativo se debe al matemático griego Arquímedes de Siracusa (aprox. 287-212 a.c.), que en su libro “Medida del círculo” calcula una cota superior y otra inferior para :

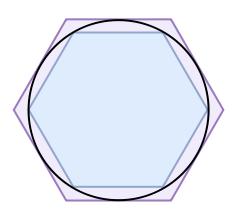
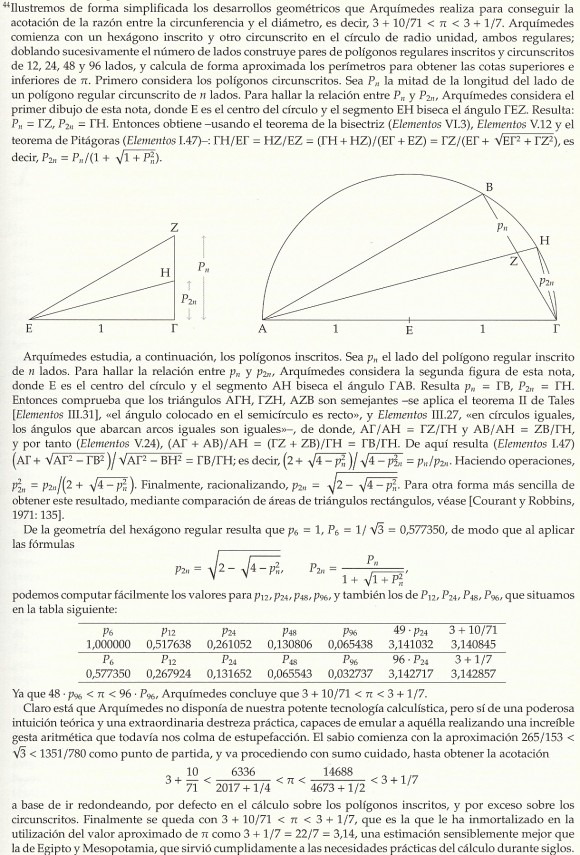
El método utilizado por Arquímedes consistía en circunscribir e inscribir un polígono de n lados en el círculo de radio unidad y calcular sus perímetros (en realidad, las longitudes de sus lados). El matemático de Siracusa empezó con hexágonos y fue doblando el número de lados de los polígonos circunscritos e inscritos, a 12, 24, 48 y 96 lados. Arquímedes hizo uso de los teoremas de Pitágoras y Tales para calcular las longitudes de los polígonos circunscritos e inscritos de lados 12, 24, 48 y 96.

En el año 2006, la Real Sociedad Matemática Española, la organización del International Congress of Mathematicians Madrid 2006 y Patrimonio Nacional editaron, bajo la dirección de Antonio J. Durán, una edición facsímil y comentada con algunas de las obras de Arquímedes. Esta es una publicación exquisita, que recomiendo a quienes estén interesados en Arquímedes o en las matemáticas en general. En particular, incluye la obra “Medida del círculo”, un trabajo breve pero de gran importancia. En él aparecen únicamente tres resultados y el primero es que “todo círculo es igual a un triángulo rectángulo cuyo radio es igual a uno de los lados que forman en ángulo recto y el perímetro es igual a la base”, que viene a ser en la formulación moderna la fórmula del área del círculo, .

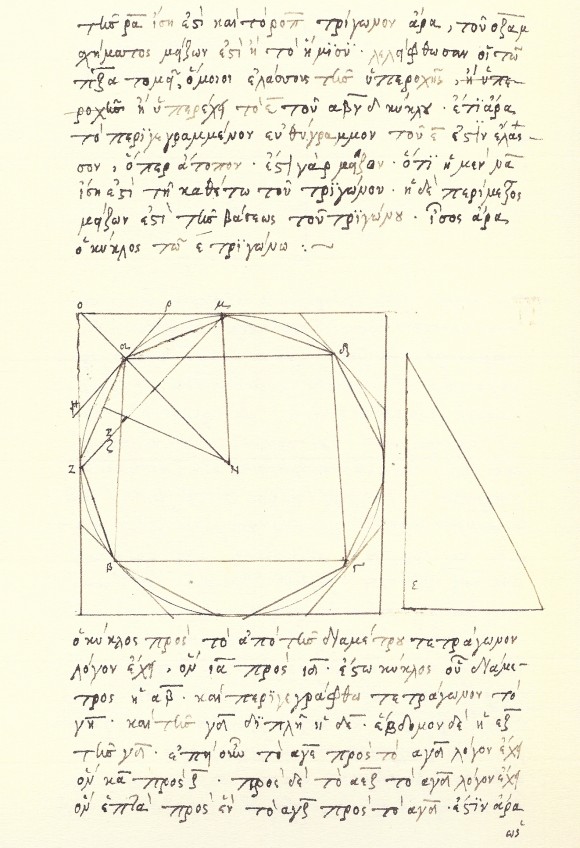
El tercer resultado de esta obra es la citada aproximación al número pi. En la edición facsímil y comentada de 2006 se explica en un lenguaje moderno en qué consistía el desarrollo de Arquímedes, en particular, el cálculo de fórmulas para las longitudes de los lados de los polígonos circunscritos e inscritos. Para quienes estén interesados mostramos a continuación dicha explicación…

Hay que tener en cuenta que hoy en día no es complicado el desarrollo de esa aproximación (incluso con polígonos de muchos más lados), sin embargo en la época de Arquímedes no tenían el sistema de numeración indoarábigo actual, era una numeración alfabética, ni nuestros algoritmos de cálculo. Además, había que aplicar aproximaciones para el cómputo de la raíz cuadrada (tema al que dedicaremos una entrada en el futuro). Por ejemplo, estimar ya era complejo.

Hubo que esperar al siglo V para un cálculo de siete decimales de pi. El matemático chino Zu Chongzhi utilizó polígonos de 12.288 lados para demostrar que pi tenía un valor entre los números 3,1415926 y 3,1415927. El uso de polígonos llegó a su punto culminante en el siglo XVII en el que el matemático alemán Ludolph van Ceulen (1540-1610), haciendo uso de polígonos con cuatro trillones de lados calculó hasta 35 decimales del número pi.

Mientras preparaba esta entrada he descubierto que Marcos Chicot ha subido un video a youtube explicando cómo calcular el número pi utilizando el teorema de Pitágoras y haciendo uso de la misma idea de Arquímedes de inscribir un polígono en el círculo de radio unidad (empezando con cuadrados).

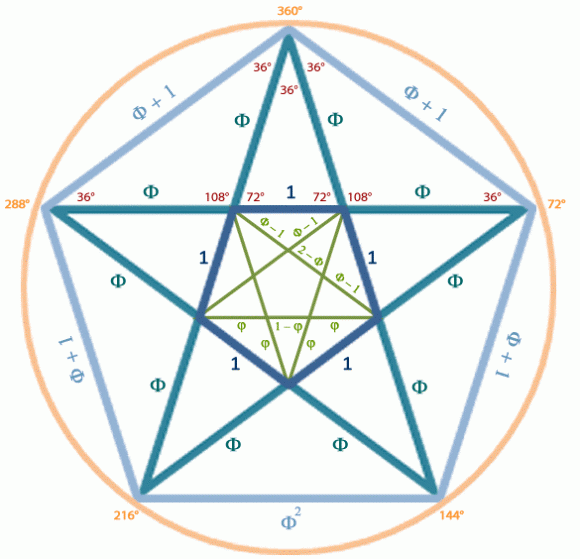
Otros dos tópicos matemáticos, relacionados entre sí, que aparecen en la novela son la sección áurea y el pentagrama pitagórico, que debemos dejar para otra ocasión.

Bibliografía

1.- Marcos Chicot, El asesinato de Pitágoras, Duomo editorial, 2013.

2.- Pedro Miguel González Urbaneja, Pitágoras, el filósofo del número, ed. Nivola (col. La matemática en sus personajes, n. 9), 2001.

3.- Pedro Miguel González Urbaneja, Pitágoras (biografías de matemáticos ilustres), www.divulgamat.net

4.- VV. AA. Arquímedes, Obras escogidas, Ed. RSME, ICM2006, Patrimonio Nacional (editor Antonio J. Durán), 2006. [Incluye la edición facsímile de las obras Sobre la esfera y el cilindro (I y II), Medida del círculo y Cuadratura de la parábola.]

5.- Alfred S. Posamentier, Ingmar Lehmann, La proporción trascendental, Ariel, 2006.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

Esta entrada participa en la Edición 4.123105625 del Carnaval de Matemáticas, cuyo blog anfitrión es http://matesnoaburridas.wordpress.com

Esta entrada participa en la VIII Edición del Carnaval de Humanidades, cuyo blog anfitrión es ::ZTFNews.