En 2014 la editorial RBA me propuso escribir el último libro de la excelente colección de divulgación de las matemáticas El mundo es matemático, en la cual ya había escrito los libros La cuarta dimensión (2010) y El sueño del mapa perfecto (2010), y les propuse escribir un libro sobre las matemáticas de los juegos, un tema apasionate y que me ha interesado desde hace tiempo. Así, el libro número 50 de la colección El mundo es matemático fue mi libro sobre matemáticas y juegos que la editorial tituló Del ajedrez a los grafos, la seriedad de las matemáticas de los juegos.

Uno de los juegos de los que hablé en este libro, en el capítulo dedicado a la combinatoria, fue el juego del Sim, un sencillo juego relacionado con la teoría de Ramsey.

El juego de Sim, perteneciente a la familia de juegos con “lapiz y papel”, es un sencillo juego que encierra una gran riqueza matemática. Fue inventado por el matemático estadounidense, experto en criptografía, Gustavus J. Simmons, mientras trabajaba en su tesis doctoral en teoría de grafos e inspirado en el estudio matemático de los números de Ramsey. El juego aparece en su artículo On the game of Sim (Journal of Recreational Mathematics, 1969).

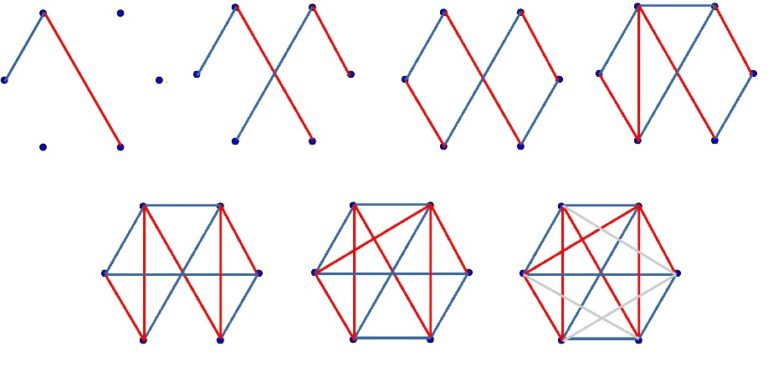
Las reglas del juego son las siguientes. Se consideran los seis puntos que determinan los vértices de un hexágono regular, pintados sobre una hoja de papel. Hay 15 formas distintas de pintar un segmento que una dos vértices de la figura (como se ve en la imagen anterior), que en conjunto forman lo que se llama el grafo completo de seis puntos, K₆. El juego de Sim es un juego para dos jugadores, cada uno de los cuales utiliza un lápiz de un color (por ejemplo, azul y rojo) para pintar, por turnos, un segmento que une dos puntos cualesquiera de la figura. Pierde el jugador que primero forme un triángulo monocolor, del color de su lápiz, siendo sus vértices puntos de la figura inicial.

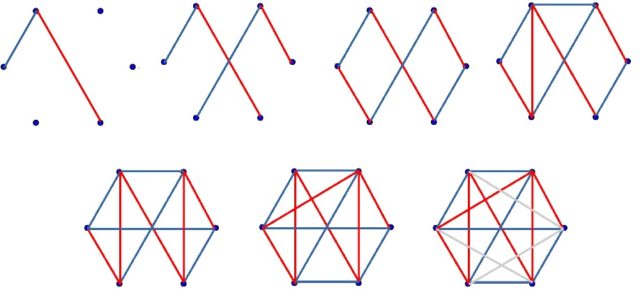
Una característica interesante del juego de Sim (el nombre parece ser que se le ocurrió a un compañero de su creador, por SIMple SIMmons y porque además recordaba al famoso juego Nim) es que no puede terminar en tablas, como demostró el propio Simmons en su artículo, haciendo uso de del conocido principio del palomar.

En este punto es recomendable recordar qué es el principio del palomar, lo cual se puede leer, con varios ejemplos y aplicaciones en las entradas del Cuaderno de Cultura Científica siguientes:

a) El principio del palomar, una potente herramienta matemática (parte 1)

b) El principio del palomar, una potente herramienta matemática (parte 2)

La demostración es la siguiente. Consideremos el grafo completo de seis puntos K₆ completamente coloreado con los dos colores, es decir, los dos jugadores han continuando pintando segmentos de forma alternada hasta completar el grafo. Tomemos un vértice cualquiera v₀. Como hay cinco líneas que pueden unir ese vértice del hexágono con los otros cinco (v₁, v₂, v₃, v₄, v₅ en la siguiente imagen), por el principio del palomar generalizado, al menos tres de ellas son del mismo color, por ejemplo, azul.

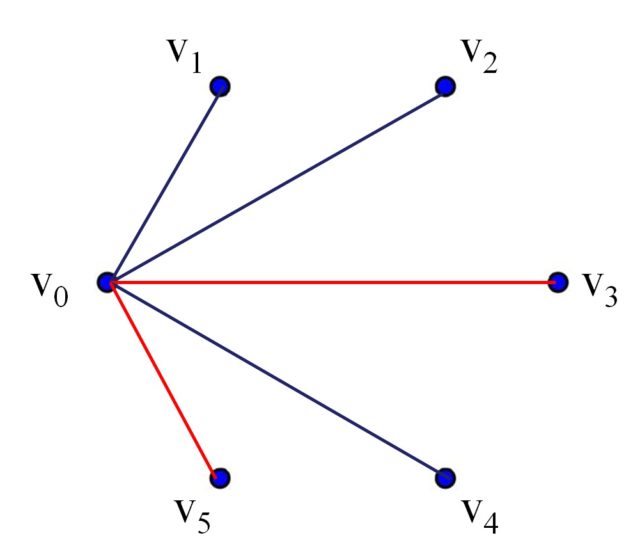
Si alguno de los tres segmentos que unen los vértices finales de esos tres segmentos azules, fuese también azul, entonces formaría un triángulo azul con los correspondientes segmentos azules que empiezan en el vértice v₀. Pero si por el contrario, ninguno de esos tres segmentos es azul, entonces los tres son rojos y forman un triángulo rojo. Por lo tanto, siempre existe un triángulo monocolor, ya sea azul o rojo. Lo cual completa la demostración.

Como consecuencia del anterior razonamiento, no existe la posibilidad de empate en el juego del Sim y alguno de los dos jugadores ganará si juega correctamente. Sin embargo, el problema de quien de los dos jugadores tiene una estrategia ganadora y cuál es esta, es bastante complejo. De hecho, Simmons no lo incluía en su artículo, y solo después de un exhaustivo análisis con ordenadores descubrió que es el segundo jugador quien tiene una estrategia ganadora, aún así, esta no es fácil de llevar a la práctica, como ocurre con otras estrategias ganadoras que han ido descubriendo los matemáticos. De las más sencillas sería la que aparece en el artículo Another strategy for SIM (Mathematics Magazine, 1978), de Leslie E. Shader.

Pero volvamos a la invención del juego de Sim. La idea que subyace al mismo se enmarca dentro de la Teoría de Ramsey, esa teoría matemática del campo de la combinatoria que viene a decirnos que el desorden completo es imposible, y más concretamente está relacionada con los números de Ramsey.

El matemático, filósofo y economista inglés Frank Plumpton Ramsey (1903-1929) demostró el resultado (conocido como Teorema de Ramsey) que es la base de la teoría que lleva su nombre en su artículo “On a problem of formal logic” (Proceedings of the London Mathematical Society, 1930) en el que estudiaba “el problema de encontrar un procedimiento para determinar la verdad o falsedad de una fórmula lógica dada”, y para ello estudiaba algunas cuestiones de combinatoria. De hecho, el famoso teorema no era más que un resultado instrumental, un lema, del artículo. Sin embargo, fueron realmente los matemáticos húngaros Paul Erdös (1913-1996) y George Szekeres (1911-2005) quienes introdujeron en 1933, trabajando en un problema geométrico, la teoría de Ramsey para grafos y la popularizaron dentro de la comunidad matemática.

Para definir los números de Ramsey recordemos que el grafo completo de n puntos K_n es el grafo con n puntos que contiene todas las aristas que unen dos de esos n puntos, y además, vamos a colorear el grafo, es decir, vamos a asignarle un color a cada arista (en general se pueden etiquetar las aristas de diferentes formas).

Dados dos números naturales r y s, se define el número de Ramsey R(r,s) como el mínimo entero n para el cualquier coloración con dos colores, por ejemplo, rojo y azul, del grafo completo de n puntos K_n, contiene un subgrafo completo K_r con todas sus aristas rojas o un subgrafo completo K_s azul.

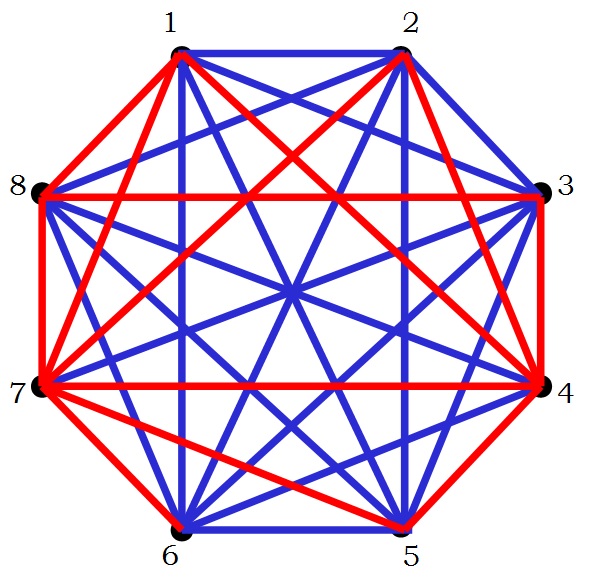
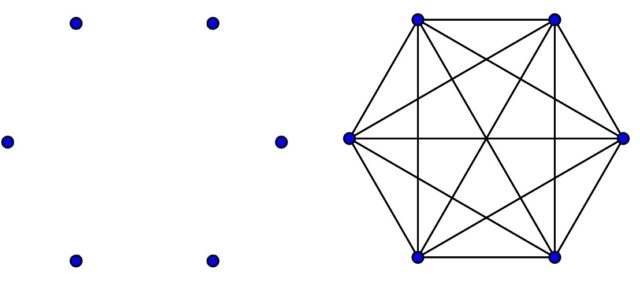
El juego de Sim está relacionado con el número de Ramsey R(3,3). La demostración de Simmons de la no existencia de tablas en el juego de su invención, es realmente una demostración de que R(3,3) ≤ 6, es decir, cualquier coloración con dos colores del grafo completo con seis puntos K₆ (y existen 2¹⁵ = 32.768 coloraciones dicromáticas) admite siempre un subgrafo completo de tres puntos, un triángulo, monocromático, ya sea, rojo o azul.

Una demostración alternativa de este resultado, que hace uso de otra interesante herramienta de la combinatoria, el conteo doble, permite obtener un resultado algo más fuerte, de hecho, al menos existen dos triángulos

Demostración: Dada una coloración dicromática, con los colores rojo y azul, del grafo completo de seis puntos, vamos a contar el número de triples de vértices x, y, z tales que el segmento (xy) es rojo y el segmento (yz) es azul.

Por una parte, para cada vértice tenemos tres opciones:

i) que todas las aristas conectadas a él sean de un solo color, luego ese vértice no será el punto medio de ninguno de esos triples;

ii) que una de las aristas sea de un color y la otras cuatro del otro, de forma que ese punto podría ser el vértice central de 4 de esos triples;

iii) que dos aristas fuesen de un color y tres del otro, de forma que podría haber 6 de esos triples.

Teniendo en cuenta que hay seis vértices, habrá como mucho 6 x 6 = 36 triples x, y, z tales que el segmento (xy) es rojo y el segmento (yz) es azul.

Por otra parte, para cada triángulo de vértices x, y, z que no sea monocromático, es decir, que tenga aristas de los dos colores, hay precisamente dos de los anteriores triples. Como hay 20 triángulos en el grafo completo de seis puntos, si ninguno de ellos fuese monocromático habría 40 triples de los que estamos buscando. Sin embargo, no puede haber más de 36, entonces existirán al menos dos triángulos monocromáticos. Y queda probada la afirmación.

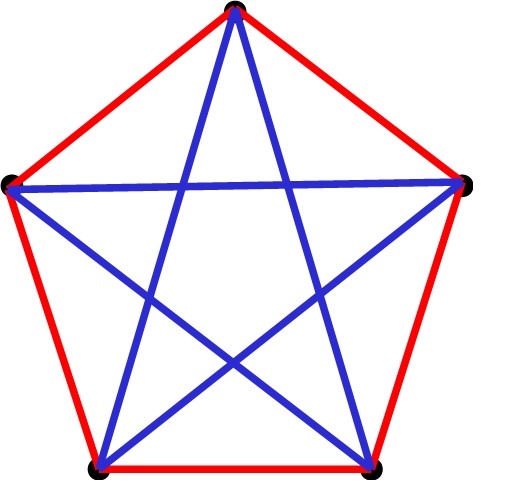
Si al hecho de que R(3,3) ≤ 6, le añadimos que existe una coloración con dos colores del grafo completo de cinco puntos K₅ (véase la anterior imagen), entonces R(3,3) > 5, y se obtiene el siguiente resultado.

Teorema (Greenwood, Gleason, 1955): R(3,3) = 6.

Este resultado se conoce también como el teorema de los amigos y extraños, puesto que se puede reformular de la siguiente forma:

En cualquier reunión con seis personas, o bien tres de ellas son conocidas (se conocen dos a dos), o bien tres de ellas son completos extraños (son desconocidas dos a dos).

Para terminar, vamos a contar una pequeña anécdota sobre el número de Ramsey R(4,4). En el libro The Princeton Companion to Mathematics (2008) se cuenta la siguiente historia del sociólogo húngaro Sandor Szalai (1912-1983). En el curso de una investigación sobre la amistad entre jóvenes, observó que para grupos de 20 jóvenes siempre podía encontrar cuatro jóvenes que fueran amigos entre sí, es decir, amigos dos a dos, o cuatro jóvenes que no fuesen amigos. Tras reflexionar sobre las posibles justificaciones sociológicas de esta observación, pensó que este parecía más un fenómeno de tipo matemático, que sociológico, y se puso en contacto con un grupo de matemáticos húngaros, entre los que estaba Erdös, quienes le confirmaron sus sospechas. Se había encontrado con la versión del teorema de los amigos y extraños correspondiente al número de Ramsey R(4,4). Su descubrimiento implicaba que R(4,4) ≤ 20. De hecho, se puede demostrar que R(4,4) = 18.

Para quienes estéis interesados en conocer más sobre los números de Ramsey podéis consultar el libro mencionado Del ajedrez a los grafos sobre las matemáticas de los juegos o el libro de combinatoria How to count, an introduction to combinatorics, que aparecen en la bibliografía.

Bibliografía

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, RBA, 2015.

2.- Gustavus J. Simmons, On the game of Sim, Journal of Recreational Mathematics 2 (n. 2), 1969, p. 66.

3.- Frank Plumpton Ramsey, On a problem of formal logic, Proceedings of the London Mathematical Society 30, 1930, p. 264-286.

4.- Timothy Gowers, June Barrow-Green, Imre Leader, The Princeton Companion to Mathematics, Princeton University Press, 2008.

5.- R. B. J. T. Allenby, Alan Slomson, How to count, an introduction to combinatorics, CRC Press, 2011.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica