La forma fractal de mapas y pulmones
Los mapas isócronos son mapas que representan tiempos: en general, el tiempo que se tarda en llegar de un lugar a otro. Distintos tonos de color corresponden a distintos valores de tiempo y, en consecuencia, dos puntos del mapa del mismo color están a la misma «distancia temporal» de otro que se haya tomado como origen.
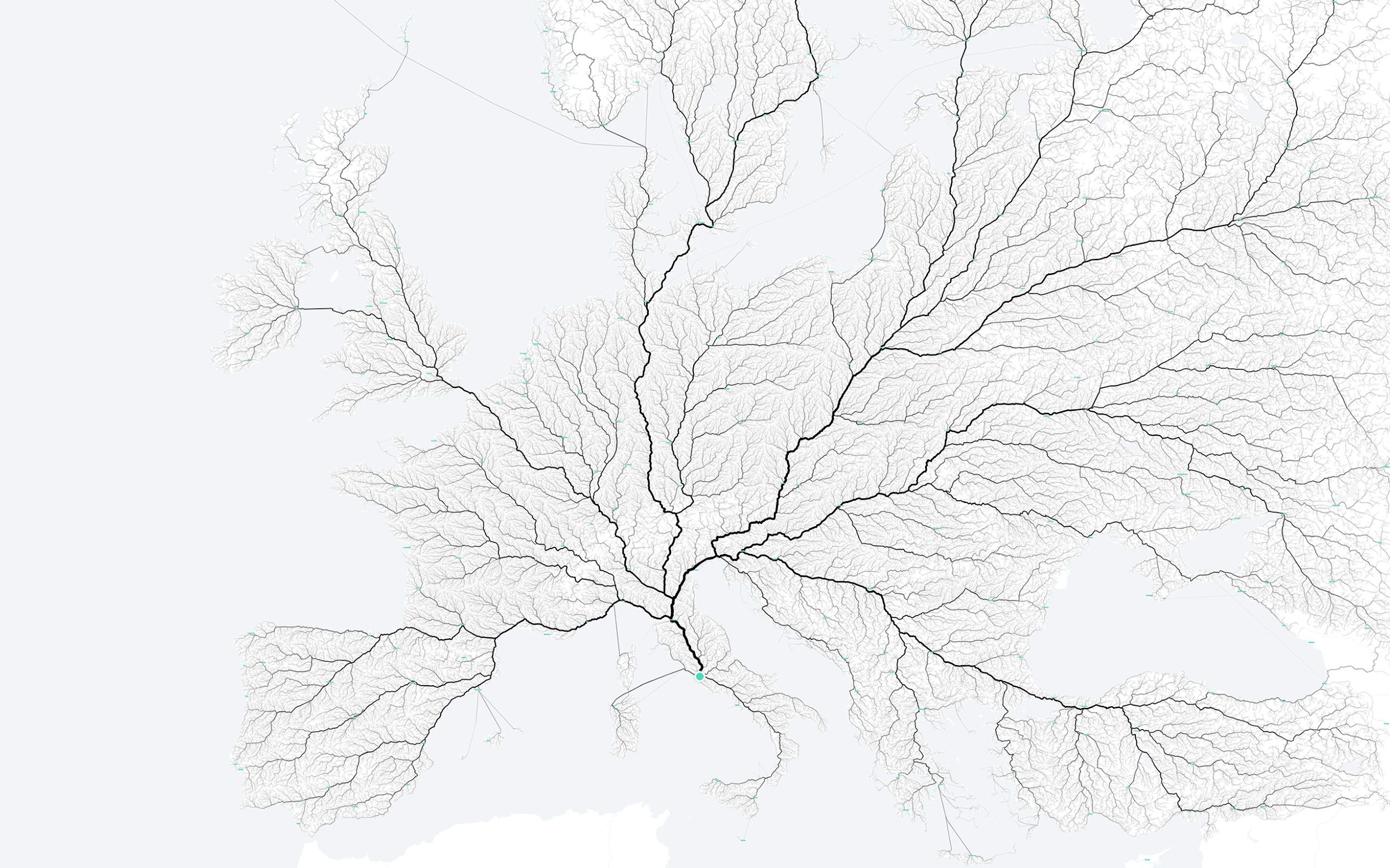
Si la superficie representada en el mapa fuese la de un terreno liso, igualmente transitable en todas las direcciones, podríamos esperar que un mapa isócrono fuese, sencillamente, una especie de diana: círculos concéntricos trazados a partir del origen elegido. En lugar de eso, el patrón que nos encontramos es este:
El vídeo, publicado por Alberto Hernando de Castro, muestra un mapa isócrono de España con origen en la Plaza Mayor de Madrid, creado con herramientas de software libre (el autor explica cómo aquí, por si queréis jugar). Pero existe una galería completa de mapas isócronos que podéis consultar: Estados Unidos, Japón, Brasil… y todos ellos tienen la misma forma. Una forma que recuerda poderosamente a la de un fractal.
No es casualidad, claro. Esta es la forma que tienen, en general, los caminos construidos por humanos mirados desde un único punto de origen (o de destino). Pero también; la forma que adopta nuestro sistema circulatorio. O las ramificaciones de nuestros pulmones. O las raíces de un árbol… Todos estos sistemas se parecen porque todos dan solución a un problema muy concreto: el problema del transporte, o de cómo cubrir una superficie (léase, un objeto de dimensión n) usando sólo líneas (de dimensión n-1).
Los fractales son, quizás, una de las estrellas pop de la matemática moderna y, francamente, no me extraña. Presentan un equilibrio intrigante de sencillez y complejidad, como los mejores puzzles de lógica: una premisa aparentemente fácil va escalando poco a poco y da lugar a una trama mucho más rica y minuciosa. Puede que su atractivo visual algo que ver con esto. O puede que nos hechice saber que ninguna de sus líneas se debe al capricho: cada una obedece un camino preciso, exacto, sin que ningún diseñador haya tenido que trazarlo, sin que ningún espectador vaya a poder recorrerlo por completo jamás.
A pesar de su encanto y su fama, los fractales son también grandes incomprendidos: la idea popular los pinta como objetos idénticos a sí mismos a distintas escalas. Sin embargo, esta no es una característica compartida por todos los fractales, sólo por los llamados autosimilares. Como definición, resultaría demasiado restrictiva, demasiado «ideal». Los fractales, en cambio, nacieron en los años 70 con la ambición de describir objetos muy reales de la naturaleza, que no podían ser delimitados por las líneas suaves a las que nos tenía acostumbrado el cálculo, o la geometría. Lo que Mandelbrot tenía en mente era capturar la idea de rugosidad: como la de la costa de Gran Bretaña o, sí, como el contorno de una carretera. Para representar esta idea matemáticamente, podemos utilizar el concepto de dimensión fractal.
Fácil y divertido. O… no tanto. Veamos qué es esto: ¿qué es una dimensión?
A todos nos suena más o menos, aunque sólo sea como salmodia, que «un punto no tiene dimensiones», que una línea recta es un objeto unidimensional, una superficie tiene dos dimensiones y los volúmenes que nos rodean ocupan un espacio de tres dimensiones (4 si consideramos el tiempo). De manera intuitiva, podemos decir que una dimensión es un parámetro de cambio que puede ser fijado mediante una coordenada. Por lo tanto, el número de dimensiones de un objeto será igual al número de coordenadas necesarias para definir un punto sobre el mismo.
Ahora bien, tomemos un fractal e intentemos poner a prueba esta idea: por simplicidad, elegiremos un fractal de los más populares, autosimilar, como el copo de nieve de Koch. A primera vista, parece ser una línea (unidimensional), por lo que debería bastar una única coordenada para definir un punto sobre ella. En este caso, claro, al no estar sobre una línea recta, nuestra coordenada será una especie de «punto kilométrico» sobre la curva.
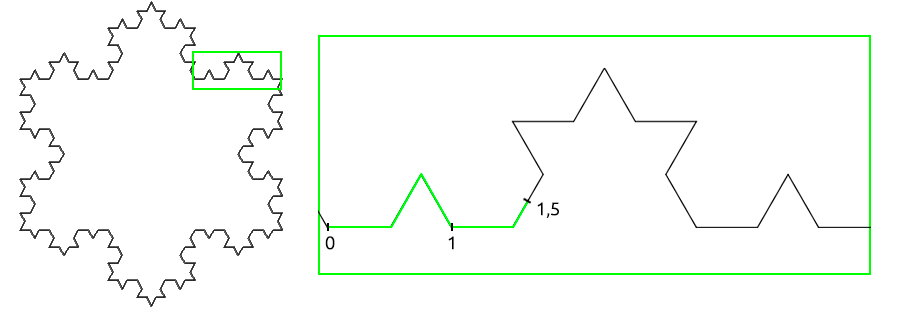
Bien, imaginemos que buscamos el punto «1,5» de la curva, siendo sus segmentos rectos de longitud 1. Para ello, hacemos zoom y nos quedamos con un fragmento lo más sencillo posible del copo de nieve. Algo como esto:

Lo dicho ¡fácil y divertido! O… no tanto. En realidad, al intentar simplificar el problema, hemos hecho una pequeña trampa. Hemos eliminado, precisamente, la rugosidad del fractal. De hecho, si nos fijamos un poco mejor y añadimos más detalle a la curva de Koch, nos encontramos con que el punto 1,5 ya no donde lo habíamos encontrado:
Y con una tercera iteración, el punto se desplaza todavía más:
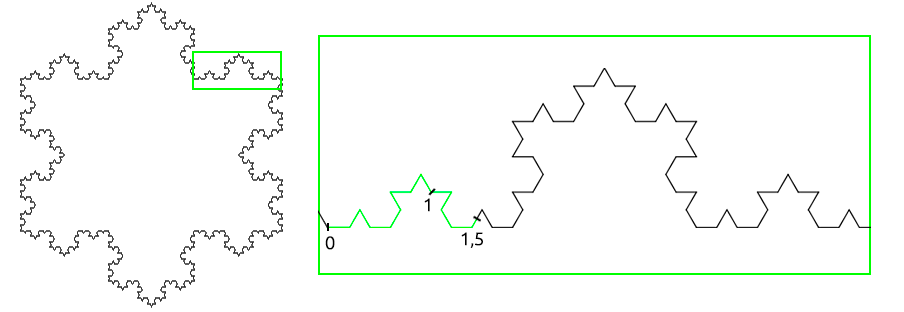
Supongo que veis adónde va a parar esto. Realmente, no es posible localizar nuestro punto de esta manera porque la longitud un fragmento cualquiera de la curva de Koch es infinito.
Como lo sería (figuradamente) el contorno de Gran Bretaña medido alrededor de cada grano de arena de su costa (o del peinado de Boris Johnson). El detalle de nuestra medida, la “escala” elegida, altera la medida misma. Esto es lo que se conoce como el efecto Richardson.
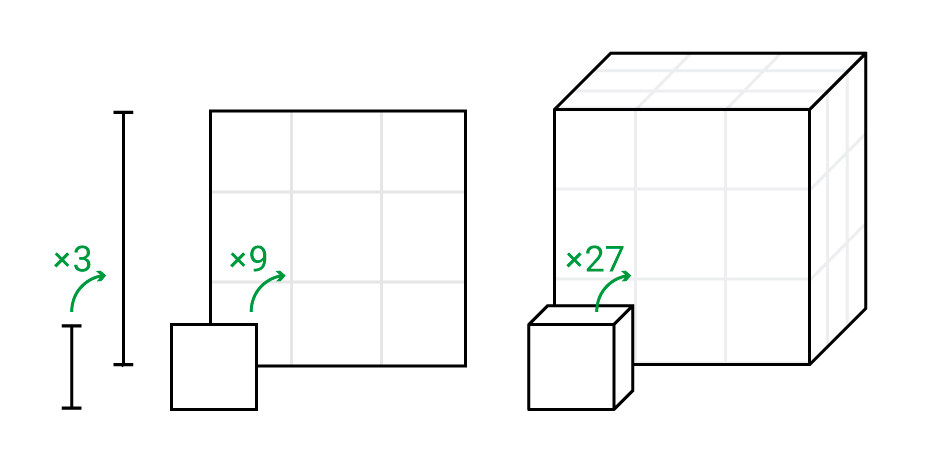
Nuestro primer intento, por tanto, no ha funcionado. Pensemos en otra manera de entender la dimensión de un objeto. Partamos, de nuevo, ejemplos conocidos: un fragmento de recta, un cuadrado, un cubo e imaginemos que queremos “pesarlos”. En este caso, se tratará de un peso imaginario, intuitivo. Podemos usar una báscula matemática de masas platónicas para medirlo, si queréis. En concreto, nos interesa saber cómo cambia la masa de estos objetos al cambiar su escala y multiplicarla por 3.
Bien: si tomamos la recta y multiplicamos su tamaño por 3, su masa se multiplicará también por 3. En el caso del cuadrado, al triplicar su escala, obtendremos un peso 9 veces mayor (dicho de otro modo: el cuadrado original cabe 9 veces en el ampliado). El cubo, pasará a pesar 27 veces más… Supongo el patrón es fácil de ver: 3=31, 9=32, 27=33. La dimensión de cada objeto nos indica a qué número debemos elevar el cambio de escala (3) para obtener el valor de la nueva masa.
¿Qué sucede entonces con la curva de Koch? Bien, en este caso, si ampliamos un fragmento de nuestro copo por 3, obtenemos un fragmento que contiene 4 veces al fragmento original. Es decir: su peso se multiplicará por 4.
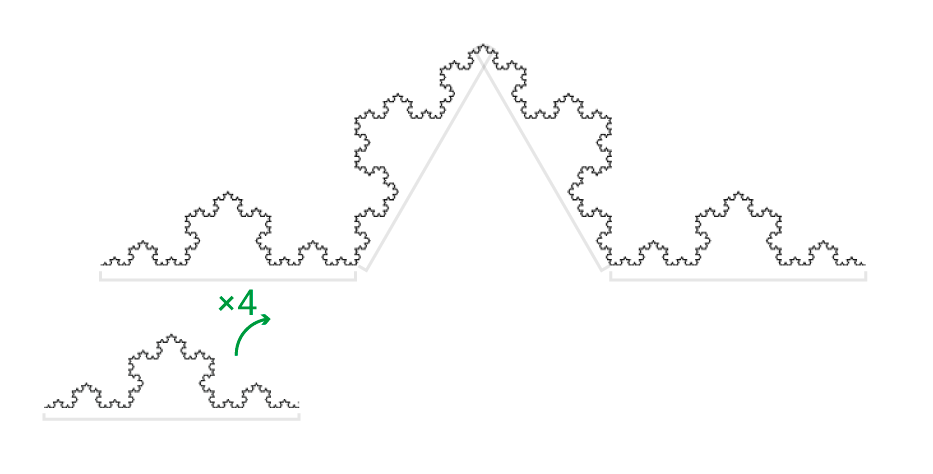
Siguiendo el razonamiento del párrafo anterior, podemos calcular cuánto vale la dimensión del fractal, encontrando el valor de este exponente (x): 3x=4
¿A cuánto hay que elevar el factor de escala (3) para que el peso se multiplique por 4? La solución de la ecuación, x = log4 / log3 nos indica que la dimensión fractal de la curva de Koch no es ni 1 ni 2: es, aproximadamente, 1,26.
Esta es la magia de los fractales: su dimensión puede ser un número no entero. El infinito que llevan en su ADN (infinitas torsiones, infinitas ramificaciones) los coloca a mitad de camino entre líneas y superficies, o superficies y volúmenes. Existen, incluso, curvas ¡de dimensión fractal 2! capaces de llenar el plano. Este es el caso de la curva de Hilbert, por ejemplo, pero existen muchas otras.

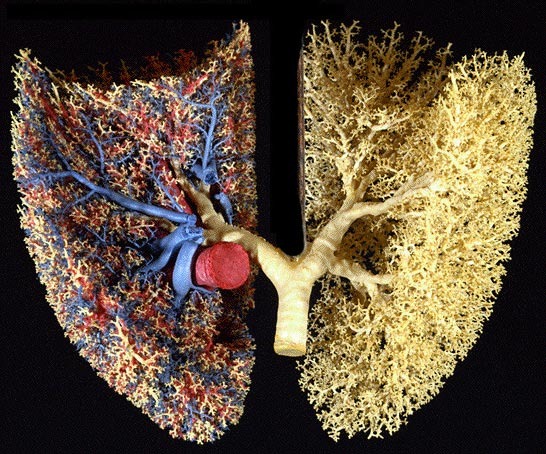
Pero volvamos a los ejemplos reales. Ciertamente, nuestros pulmones no se ramifican de manera infinita ni tienen una masa platónica. Sin embargo, es precisamente su parecido con un fractal lo que les permite maximizar su superficie siguiendo un patrón de crecimiento relativamente sencillo (similar a distintas escalas). Los pulmones, como árboles invertidos (y los árboles, como pulmones invertidos), intercambian gases en la punta de cada rama, donde se encuentran los alvéolos (las hojas). La cantidad de gases que consiguen aprovechar es directamente proporcional a su superficie total. Y aquí es donde viene el dato sorprendente: aunque el volumen de los pulmones humanos es apenas de unos 4 a 6 litros, su superficie ronda los 140 metros cuadrados1, algo más de media cancha de tenis. En esto consiste, precisamente, la idea de rugosidad. Para cuantificarla, eso sí, pueden tomarse distintas aproximaciones: en el caso de los pulmones, la dimensión fractal varía, según distintos autores, entre 2,26 y 2,882.
Volviendo a las líneas del precioso mapa isócrono que, sin quererlo, se han ramificado hasta dar forma a esta digresión: se ha estimado que podrían tener una dimensión de 1,83. Resulta difícil asegurar si la fractalidad de estas carreteras se debe, quizás, a la rugosidad del propio terreno sobre el que se construyen. O si el truco radica en tomar un punto de origen sobre una red mucho más compleja. En cualquier caso, es bonito pensar que nuestros caminos son, de hecho, equivalentes a pulmones, o al sistema circulatorio de un organismo inmenso del que, sin saberlo, formamos parte. Un organismo vivo que nosotros mismos hemos ido construyendo.
Bonus track: Este es el aspecto de los ríos y sus afluentes
Referencias:
1 E.N. Marieb, K.N. Hoehn. Human anatomy and physiology.
2 K. Lamrini Uahabi and M. Atounti. New approach to the calculation of fractal dimension of the lungs
3 P. Pavón et al. Multifractal approach for comparing road transport network geometry: The case of Spain
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
Marian
Hola, Almudena.
Una curiosidad, ¿alguna razón en concreto para que la foto de los pulmones humanos esté del revés (como lo corrobora su pie de foto)?
Por otra parte, la entrada me ha resultado muy interesante.
Saludos cordiales,
Marian.
Almudena
¡Hola! Se quiere reforzar su similitud con los árboles. «Los pulmones, como árboles invertidos (y los árboles, como pulmones invertidos), intercambian gases en la punta de cada rama, donde se encuentran los alvéolos (las hojas)». Para la próxima, incluyo la referencia en el pie.
¡Muchas gracias!
puratura
[…] leyendo en La forma fractal de mapas y pulmones (Cuaderno de Cultura […]
Hitos en la red #234 | La manzana podrida
[…] de un chiste pero no lo es: ¿en qué se parece un mapa de carreteras a unos pulmones? La forma fractal de mapas y pulmones por Almudena M. […]
Hitos en la red #234 – Enlaces Covalentes
[…] de un chiste pero no lo es: ¿en qué se parece un mapa de carreteras a unos pulmones? La forma fractal de mapas y pulmones por Almudena M. […]
El mapa del cólera de John Snow — Cuaderno de Cultura Científica
[…] la distancia en tiempo, o distancia “caminada” a cada fuente (similar a la que registran los mapas isócronos). Para ello, tomó cuerda (para medir distancias sobre una trayectoria sinuosa) y un lápiz, y […]
El mapa del cólera de John Snow – Fluceando
[…] la distancia en tiempo, o distancia “caminada” a cada fuente (similar a la que registran los mapas isócronos). Para ello, tomó cuerda (para medir distancias sobre una trayectoria sinuosa) y un lápiz, y […]