En esta entrada del Cuaderno de Cultura Científica nos adentramos una vez más en el mundo del cómic y su relación con las matemáticas. En concreto, vamos a comentar las referencias matemáticas que aparecen en Promethea (1999-2005), del guionista Alan Moore y el dibujante James H. Williams III.

El guion de esta serie de cómics está firmado por el escritor británico Alan Moore, considerado por muchas personas como el mejor guionista de cómics en lengua inglesa. Alan Moore es el autor de grandes cómics como V de Vendetta (1982 –a lo largo de esta entrada, en los cómics indicaremos el año de aparición del primer número de la serie–), La cosa del pantano (1982), Watchmen (1986), Batman, la broma asesina (1988), Desde el infierno (1991) o La liga de los hombres extraordinarios (1999). Este controvertido escritor inglés cree en el ocultismo, de hecho, es seguidor del ocultista inglés Aleister Crowley (1875-1947), en la cábala y en otras creencias esotéricas, así mismo ha declarado ser un mago ceremonial. De hecho, la religión, el ocultismo y la magia, tan importantes para Alan Moore, son una parte fundamental de la historia que se cuenta en Promethea.

Pero centrándonos en las matemáticas, a lo largo de este cómic podemos observar que también las matemáticas son un tema que le interesa personalmente, ya que incluye varias referencias a esta ciencia. Aunque una prueba directa del interés de Alan Moore por la ciencia de Pitágoras la podemos encontrar en su proyecto de cómic Big Numbers (Grandes números). Tras el enorme éxito de Watchmen, este escritor de guiones de cómic decidió embarcarse, con el dibujante estadounidense Bill Sienkiewicz, en el proyecto Big Numbers (cuyo título original era The Mandelbrot Set), del que solo se publicarían los dos primeros números en 1990 y parte del tercero. La temática de esta serie estaba relacionada con las matemáticas, la teoría del caos y la economía, y su protagonista era el matemático Benoit Mandelbrot.

El dibujo de Promethea es del artista y escritor estadounidense James H. Williams III, autor de la ilustración de muchísimos cómics, entre los que citaremos algunos como Chase (1998, con Dan Curtis Johnson), Desolation Jones (2005, con Warren Ellis), Batwoman (2009, también co-guionista con W. Haden Blackman) o Sandman: obertura (2013, con Neil Gaiman).

Promethea es una serie de cómic formada por 32 números, escrita por Alan Moore y dibujada por James H. Williams III, que se publicó entre los años 1999 y 2005 en America’s Best Comics, el sello editorial de WildStorm (DC Comics) creado por Alan Moore en 1999. Es un cómic con una gran experimentación visual y artística, que experimenta con diferentes estilos de dibujo, con diferentes estructuras de sus páginas, que juega con la simetría y los colores. Recibió varios reconocimientos, en los prestigiosos Premio Eisner y Premio Harvey del mundo del cómic.

La protagonista del cómic Promethea es una estudiante universitaria, Sophie Bangs, que vive en la ciudad de Nueva York (de un mundo ucrónico en el año 1999, el mismo año de su publicación), que debe hacer un trabajo sobre una mujer mitológica, Promethea. Al estudiar este personaje mitológico acabará descubriendo que también es un personaje real, que ha existido desde la antigüedad y que distintas personas a lo largo de la historia se han convertido en la Promethea real, uniendo su mente a la de la Promethea mitológica, produciéndose la transformación mediante la creación de obras de ficción (cómic, novela, poesía,…) sobre Promethea. Sophie Bangs acabará convirtiéndose en la siguiente Promethea, destinada a llevar el Apocalipsis al mundo, para lo cual primero deberá emprender un viaje, a través del árbol de la vida, cuyo objetivo es el conocimiento.

El cómic juega con la idea de que la realidad está compuesta del mundo real, que es el mundo material, y el mundo de la imaginación, la Inmateria. Todo el viaje de conocimiento de la nueva Promethea nos lleva a través del ocultismo, la cábala, el árbol de la vida, el tarot, la magia y otros temas similares, que forman parte de las creencias de su autor Alan Moore.

Una de las primeras cosas que llama la atención cuando se empieza a leer este cómic es la estructura nada convencional y experimental de sus viñetas. Nos podemos encontrar estructuras de lo más variadas, con un gran derroche de imaginación y arte, adaptándolas a la historia que se cuenta y dibujando, en muchas ocasiones, dobles páginas con una estructura global impactante.

La simetría también juega un papel importante en muchas de ellas. Por ejemplo, en la imagen anterior, vemos como la primera doble cara tiene una estructura con una simetría especular respecto al centro, mientras que en la segunda es una simetría rotacional. Por otra parte, en la tercera doble página tiene una estructura circular y en la cuarta una estructura especular, pero jugando con los contrarios y con dos colores para ellos. Aunque en otros casos se realizan estructuras más imaginativas y libres, como las dos últimas dobles páginas de la imagen anterior. Otro ejemplo interesante es la doble página con la banda de Moebius (se muestra en una imagen más abajo) que tiene el fondo con una simetría especular entre la parte de arriba, el día, y la parte de abajo, la noche, al mismo tiempo que la imagen principal es una banda de Moebius en piedra, dibujada de forma simétrica, imitando además la forma del infinito.

La primera imagen con una referencia matemática clara, de algunos signos matemáticos, aparece en el primer tomo (de los cinco tomos que conforman la edición que se realizó tras completarse la publicación de los 32 números originales), después de que la protagonista Sophie Bangs se haya convertido ya en la nueva Promethea. Entonces visita, en la Inmateria, a las anteriores Prometheas que han existido a lo largo de la historia y estas le explican que la realidad está compuesta de algo más que el mundo material, que solo es “la décima parte de un iceberg que resulta visible por encima de la superficie del mar de la realidad”, y en qué consiste el mundo inmaterial. Le empiezan explicando que primero está la esfera lunar que es la de la imaginación, el sueño, la ficción, las fantasías sexuales y el inconsciente. Y sigue la explicación “Más allá de la esfera lunar se encuentra el terreno de Mercurio, la tierra del intelecto y la ciencia, de la magia y el lenguaje”, y se acompaña con imágenes y símbolos matemáticos: números, el signo para el infinito, el número pi, polígonos (triángulo y pentágono), etc.

Otra de las Prometheas le dice a Sophie “la razón y el discernimiento acaban con las gilipolleces” y “la razón acaba con los espejismos y las alucinaciones”, lo cual no deja de ser curioso si se tiene en cuenta la importancia del ocultismo, la magia, la numerología, la cábala o el tarot en esta historia.

De hecho, en relación con el ocultismo, la astrología y otras creencias similares que el guionista Alan Moore incorpora a la historia de este cómic, se incluyen en Promethea tanto objetos geométricos, relacionados con la llamada geometría sagrada, como números o estructuras numéricas, conectadas con la numerología, el árbol de la vida o el tarot. Se incluyen dibujos de objetos geométricos sencillos, como el círculo, el triángulo, el cuadrado, el pentagrama y otras estrellas, la espiral, el cubo, algún poliedro, la esfera, algunos otros más curiosos como la banda de Moebius y curvas hipotrocoides dibujadas con un espirógrafo y otros más complejos, como los fractales. Aparecen los números de las cartas del tarot, los números de los diez sefirot (sefirá en singular y sefirot en plural), o atributos, y los 22 senderos del árbol de la vida, por los que viajan las Prometheas de Sophie y Margaret, que fue quien encarnó a la anterior Promethea y le ha pasado el testigo a Sophie, el número pi, cuadrados mágicos o el recorrido de un caballo en el tablero de ajedrez. De algunos de ellos hablaremos a continuación.

En el tomo 2 de Promethea, cuando se están describiendo las cartas del tarot se incluye la imagen de un cuadrado mágico. Como vimos en las entradas del Cuaderno de Cultura Científica sobre la novela gráfica Habibi (véase la bibliografía al final de la entrada), los cuadrados mágicos ya se conocían desde la antigüedad (quizás más allá del año 2.200 a.n.e.), y se les relacionaba con los planetas y con la alquimia, con la magia y la astrología, con la numerología, y también se utilizaban para sanar o como amuletos.

Recordemos que un cuadrado mágico de orden n, es una distribución de los primeros n² números (para orden 3, los 9 primeros números, 1, 2, 3, 4, 5, 6, 7, 8, 9; y para orden 4, del 1 al 16), sobre las casillas de un cuadrado n x n, (para orden 3, un cuadrado 3 x 3, o para orden 4 un cuadrado 4 x 4), de forma que la suma de cada fila, cada columna y cada diagonal sea siempre la misma (para orden 3 es 15 y para orden 4 es 34); a ese número se le llama constante del cuadrado mágico.

En este cómic se incluye un cuadrado mágico de orden 4, sobre el que podemos observar que la suma de cada fila, columna o diagonal es siempre 34 (por ejemplo, primera fila, 1 + 15 + 14 + 4 = 34, primera columna, 1 + 12 + 8 + 13 = 34, primera diagonal, 1 + 6 + 11 + 16 = 34). Este cuadrado mágico es el que en la alquimia europea se relacionaba con el planeta Júpiter y con el metal estaño (como se comentaba en la entrada sobre la novela gráfica Habibi).

El siguiente elemento matemático que aparece en esta serie de cómic y que me gustaría mencionar es el fractal conocido como conjunto de Mandelbrot. El cielo aparentemente estrellado que se ve en parte del recorrido de Sophie-Promethea por los mundos del árbol de la vida es un cielo en el que se observan trozos del fractal de Mandelbrot.

Recodemos brevemente en qué consiste este fractal. Los números complejos son una extensión de los números reales formada por los elementos (números) de la forma a + bi, donde a y b son números reales, e i es la unidad imaginaria cuyo cuadrado es – 1 (es decir, i es la raíz cuadrada de – 1). Cada número complejo a + bi se puede identificar con el punto (a, b) del plano coordenado, por lo que hablaremos de esta visualización de los números complejos, como el plano complejo. Veamos cómo se define el conjunto de Mandelbrot.

Dado un número complejo c (por lo tanto, también nos indica un punto del plano coordenado), se toma la sucesión recursiva siguiente:

Si la sucesión se va hacia infinito, entonces el elemento del plano complejo c no pertenece al conjunto de Mandelbrot, mientras que, si se mantiene acotada, entonces c es un punto del conjunto de Mandelbrot. Veamos algunos ejemplos:

i) para c = 0, la sucesión es constante igual a 0, luego acotada y 0, el origen (0,0) del plano complejo, pertenece al conjunto de Mandelbrot;

ii) para c = 1, la sucesión es 0, 1, 2, 5, 26, 677,… que se va al infinito, luego 1, en el plano el punto (1, 0), no pertenece al conjunto de Mandelbrot;

iii) para c = – 1, la sucesión es 0, – 1, 0, – 1,… luego está acotada y el – 1, el punto (– 1, 0) del plano complejo, pertenece al conjunto de Mandelbrot;

iv) para c = i, la sucesión es 0, i, – 1 + i, – i, – 1 + i,… que está acotada, luego i, el punto (0, 1), pertenece al conjunto de Mandelbrot;

v) para c = 2i, la sucesión es 0, 2i, – 4 + 2i, 12 – 14i,… que no está acotada, luego 2i, el punto (0, 2), no pertenece al conjunto de Mandelbrot.

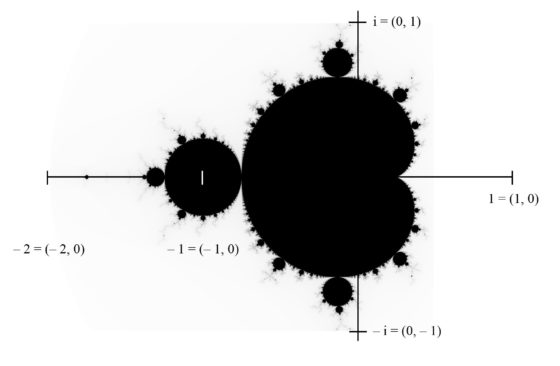
En la imagen anterior, los puntos c del plano complejo que están en el conjunto de Mandelbrot, es decir, la serie no diverge, aparecen representados/pintados en negro, mientras que los que no están en el mismo están en blanco.

El fractal se suele representar utilizando diferentes colores, no solo blanco y negro, utilizando un algoritmo de escape, es decir, el color está determinado por la rapidez que la sucesión se escapa hacia infinito (es decir, que el módulo del número complejo de la sucesión es mayor que una cantidad dada). Así, en la siguiente imagen el conjunto de Mandelbrot sigue estando de negro mientras que el rojo indica lo rápido (más oscuro) o lento (más claro), que la sucesión recursiva se marcha hacia infinito, su módulo se hace muy grande. El color más cercano al blanco es porque para esos puntos del plano complejo la sucesión ha tardado mucho en despegarse.

Una de las peculiaridades de los fractales, en particular, del fractal de Mandelbrot, es que son “autosemejantes”, son más o menos invariantes a diferentes escalas. Si realizamos un zoom de alguna de las zonas frontera del conjunto de Mandelbrot, recuperaremos en algún momento la estructura del conjunto original. Por ejemplo, en la siguiente imagen hemos realizado un zoom de la parte de arriba de la anterior imagen (recuadro morado) y de nuevo otro zoom de otra zona de arriba de la nueva imagen (recuadro morado), obteniendo de nuevo la imagen del conjunto de Mandelbrot.

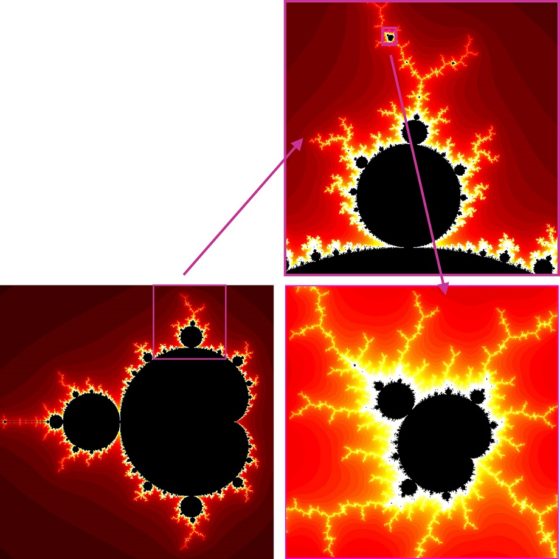
Otra de las maravillas del fractal de Mandelbrot, y de otros fractales, es que al hacer zoom se van descubriendo hermosas estructuras, como la siguiente imagen obtenida al hacer zoom sobre el conjunto de Mandelbrot.

En el cómic se observan sobre el cielo “estrellado” esa especie de dendritas que salen del conjunto de Mandelbrot y que podemos ver, por ejemplo, en la anterior imagen de un detalle del fractal.

En la siguiente imagen de una doble página del cómic se pueden observar esas dendritas del fractal de Mandelbrot (algunas de ellas marcadas en amarillo para distinguirlas mejor), e incluso podemos observar una imagen obtenida después de diferentes zooms en la que se aprecia la forma del conjunto de Mandelbrot (marcada en rojo).

Como comentábamos en la tercera parte de la entrada del Cuaderno de Cultura Científica dedicada a la novela gráfica Habibi, los alquimistas europeos relacionaban Mercurio (y el metal del mismo nombre), con el siguiente cuadrado mágico de orden 8 (cuya constante es 260). Este es muy fácil de obtener como se explica en Habibi y los cuadrados mágicos II.

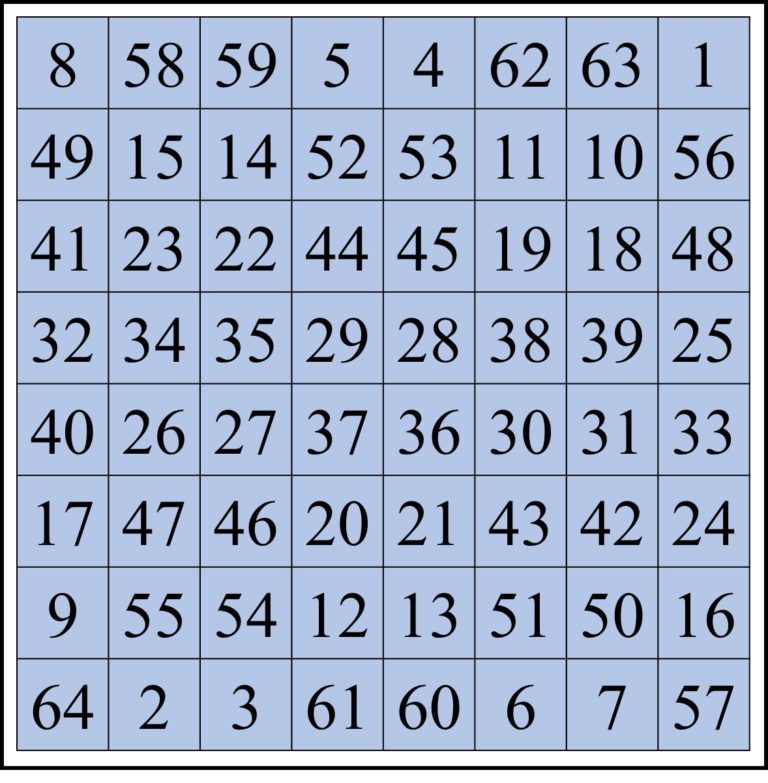
Por este motivo, cuando las dos Prometheas, las encarnadas por Sophie y Barbara, llegan a la octava sefirá del árbol de la vida, del guionista Alan Moore y el dibujante James H. Williams III lo ilustran dibujando el cuadrado mágico de orden 8 relacionado con Mercurio.

Entonces, llega otra aportación matemática muy interesante, la utilización de la banda de Moebius dentro de la historia. Las Prometheas de Sophie y Barbara están recorriendo el lugar de la octava sefirá, cuando de repente se encuentran caminando en un camino con forma de banda de Moebius y, por lo tanto, en un paseo infinito.

Recordemos que una banda de Moebius es una superficie con una única cara. Es una banda retorcida que podemos construir de forma sencilla de la siguiente forma. Si tomamos una tira de papel y pegamos los extremos se obtiene una banda normal con dos caras, pero si primero giramos uno de los extremos del papel media vuelta y después juntamos los extremos se obtiene la banda de Moebius, una superficie que solo tiene una cara.

Es una sencilla construcción que puede realizarse con facilidad mientras se lee esta entrada del Cuaderno de Cultura Científica. ¿Cómo comprobar que, efectivamente, sólo tiene una cara? Si tenemos nuestra banda realizada con papel, podemos pintar con un rotulador, empezar en un punto y pintar en una dirección, y continuar pintando hasta llegar al punto en el que empezamos, entonces podemos comprobar que está pintada toda la banda, luego solo hay una cara. No ocurre lo mismo con una banda normal, ya que pintaremos la parte interior o la exterior, dependiendo de donde pongamos el rotulador, ya que tiene dos caras.

Una de las obras del artista neerlandés M. C. Escher (1898-1972) es precisamente una banda de Moebius que está siendo recorrida por hormigas, en un camino sin fin que quiere representar esta propiedad de que tiene una única cara.

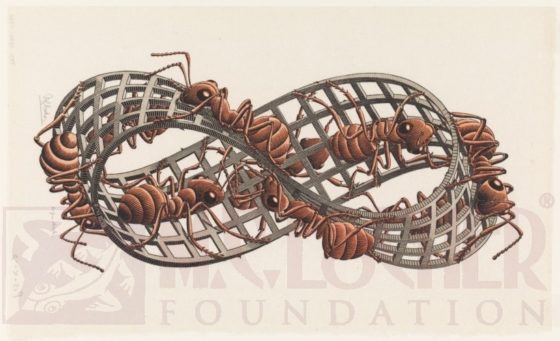
La banda de Moebius que aparece en este cómic es un camino de arena y piedra recorrido por las dos Prometheas, al igual que las hormigas rojas recorren la banda de Escher. Aunque el dibujante J. H. Williams III ha dibujado una banda más estrecha, más esbelta, que le permite trazar la banda de una sola cara de forma que parezca el símbolo del infinito. De esta forma nos transmite la idea de un camino infinito incluso antes de que nos percatemos de que es una banda de Moebius.

En esta ilustración a doble página de la banda de Moebius, como un camino, vemos al mismo tiempo a las dos Prometheas en diferentes puntos de la misma, mientras caminan y conversan. Es como si viéramos el espacio-tiempo continuo (cuarta dimensión) del recorrido que realizan. De hecho, ellas mismas pueden verse y escucharse en ese espacio-tiempo continuo (aunque más que continuo, deberíamos decir que es discreto, para ser de esta forma fiel a lo dibujado) en diferentes momentos: “… oigo algo raro, como gente que habla debajo de nosotras…”, “¡… mira ese puente de ahí delante! ¡Somos nosotras, Sophie! ¡Nosotras hace cinco minutos!”, “¡Por Dios, Barbara, tienes razón! Esas somos nosotras caminando por la parte de abajo. Esto debe de ser una banda de Möbius”, “… el infinito es un concepto aterrador. ¿Cómo vamos a salir de este camino?”.

La siguiente referencia matemática destacada se produce cuando las Prometheas de Sophie y Barbara conversan con Hermes/Mercurio (los nombres que recibe este Dios según la mitología griega o romana), quien les plantea el conocido problema del recorrido del caballo en el tablero de ajedrez. El problema consiste en recorrer con un caballo (utilizando su movimiento en L) todas las casillas de un tablero de ajedrez sin pasar dos veces por la misma y empezando en una casilla dada. Y se muestra la imagen de una de las soluciones del problema.

La Promethea-Barbara le dice a la Promethea-Sophie “¡Sophie, volvemos a estar en un cuadrado mágico!” y ella le contesta “… pero este es un cuadrado mágico distinto. Los números están en un orden diferente”.

Los números que aparecen en el tablero de ajedrez nos están indicando el orden de recorrido de las casillas del tablero. La primera casilla es el 1, la siguiente el 2, así hasta la casilla 64. En el libro Del ajedrez a los grafos (RBA, 2015) podéis leer más sobre el problema del recorrido del caballo en el tablero de ajedrez.

El matemático suizo Leonhard Euler (1707-1783), que fue el primero en realizar un análisis matemático riguroso del juego, se planteó además el problema de encontrar un recorrido por el tablero de ajedrez de forma que los números del orden de recorrido formen un cuadrado mágico. Sin embargo, Euler solamente pudo obtener un recorrido que generara un cuadrado semi-mágico, es decir, la suma de cada fila y de cada columna, es siempre la misma, pero no ocurre lo mismo con las diagonales.

Como se explica en el artículo There Are No Magic Knight’s Tours on the Chessboard en Wolfram Mathworld, en 2003, haciendo uso de la fuerza de la computación, J. C. Meyrignac y Guenter Stertenbrink demostraron que existían 140 cuadrados semi-mágicos obtenidos mediante el recorrido del caballo en el tablero de ajedrez, pero ninguno de ellos era mágico. Por lo tanto, el que aparece en Promethea será un cuadrado semi-mágico, pero no mágico.

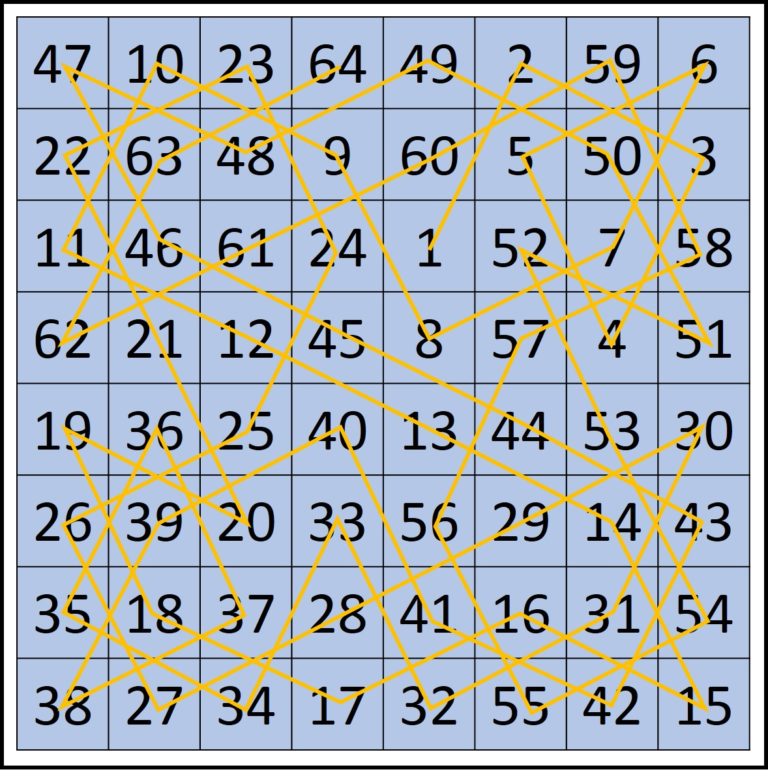
He reconstruido el recorrido del caballo sobre el tablero de ajedrez que aparece en el cómic y es el que aparece en la siguiente imagen. Podemos observar que efectivamente el recorrido del caballo acaba por pasar por todas las casillas sin repetir ninguna y que además los números del recorrido son tales que los que están en cada fila, respectivamente, columna, suman siempre 260, es decir, es un cuadrado semi-mágico, ya que las diagonales no suman lo mismo, 304 y 232.

E incluso mencionan al número pi cuando están en un lugar entre las sefirot 3 y 4 del árbol de la vida. Se produce el siguiente diálogo:

Barbara: ¿Desde cuándo once está entre el tres y el cuatro?

Sophie: Ya, eso no cuadra ¿verdad? Tenemos la esfera tercera a un extremo del abismo, la cuarta en el otro, y la undécima en medio. Pero claro, no existe un número entre el tres y el cuatro. Así que tampoco encajaría ningún otro número.

Barbara: ¿Qué hay de pi?

Sophie: ¿Pi? Pero si pi ni siquiera puede ser calculado con exactitud, así que no es un número de verdad.

Barbara: Bueno, entonces eso lo convierte en un número falso, ¿no? En una sephira falsa. Además, se encuentra entre el tres y el cuatro. ¿Y no es tres coma diecisiete no sé cuántos?

Sophie: Dios, tienes razón. Y si le quitamos la barra transversal de arriba al símbolo de pi, nos sale un “once”. Además, podríamos estar calculando eternamente los decimales de pi, así que imagino que al abismo le ocurre lo mismo, es insondable…

Aunque los elementos matemáticos, tanto objetos geométricos, como estructuras de números, que aparecen en esta serie de cómic están relacionados con el esoterismo y la magia, lo cierto es que sus autores introducen cuestiones muy interesantes y con una profundidad matemática mayor de lo que a priori parece. Aunque de todas las cuestiones matemáticas que aparecen, para mí la más llamativa y mejor integrada es la utilización que se hace de la banda de Moebius.

Bibliografía

1.- Wikipedia: Promethea

2.- Raúl Ibáñez, Habibi y los cuadrados mágicos I, Cuaderno de Cultura Científica, 2013.

3.- Raúl Ibáñez, Habibi y los cuadrados mágicos II, Cuaderno de Cultura Científica, 2013.

4.- Raúl Ibáñez, Habibi y los cuadrados mágicos III, Cuaderno de Cultura Científica, 2013.

5.- Wikipedia: Mandelbrot set

6.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

7.- Eric W. Weisstein, There Are No Magic Knight’s Tours on the Chessboard

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica