Después de nuestra anterior entrada del Cuaderno de Cultura Científica, ¡Música, matemática!, que tenía como objetivo mostrar algunas canciones, de grupos con diferentes estilos musicales, dedicadas a objetos matemáticos, como los números primos, la sucesión de Fibonacci, el número Pi o el conjunto de Mandelbrot, en esta nueva entrada nuestra intención es centrarnos en algunos resultados matemáticos, como los teoremas de Pitágoras, Tales o Fermat, la conjetura de Goldbach, la hipótesis de Riemann y el teorema de Arquímedes.
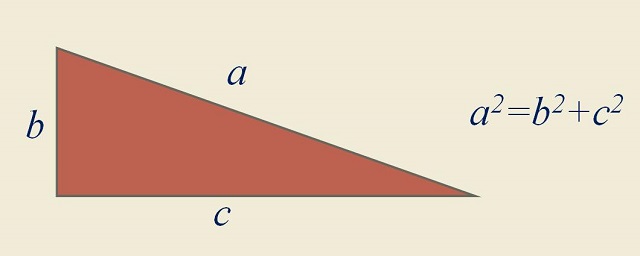
Como no podía ser de otra forma, empezaremos esta entrada con el popular teorema de Pitágoras. El enunciado de este teorema geométrico, aunque de sobra conocido, dice que “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”, la famosa expresión a2 = b2 + c2, si c y b son los catetos y a la hipotenusa.
Para aquellas personas que estén interesadas en conocer más sobre el teorema de Pitágoras, hemos dedicado varias entradas al mismo, como Pitágoras sin palabras, Cultura pitagórica: arte, Sin noticias de Pitágoras (Pitágoras en la literatura) o El teorema de Pitágoras en el arte.
La primera canción de esta entrada, relacionada con el teorema de Pitágoras, es un tema clásico del rock español, Pitágoras, que versionaron grupos como Los Milos (1961), Lolita Garrido (1961), Los Hooligans (1964) o, más recientemente, el grupo valenciano Seguridad Social (2000), conocido por temas como Chiquilla o Quiero tener tu presencia. Aunque no mucha gente sabe que este tema es una canción del cantante italiano Adriano Celentano (1960).
Aquí podemos escuchar la potente versión de Seguridad Social: Pitágoras.
La letra de la canción dice lo siguiente.
La suma de los cuadrados encima de los catetos, // Es igual al cuadrado de la hipotenusa… // Pitágoras, Pitágoras, // Hoy quiero pedirte un favor: // Enséñame el sistema y el nuevo teorema // De cualquier problema de amor. // Si laten dos corazones unidos por simpatía, // Su ritmo se multiplica al cuadrado… // Pitágoras, Pitágoras, // Suspende tu meditación, // Y con tu teorema, resuélveme el problema, // Que tengo yo en mi corazón. // El ritmo de una pareja que baila con fantasía, // Anima el ambiente a la hipotenusa… // Pitágoras, Pitágoras, // Era un sabio de eterno valor, // Enséñame el sistema y el nuevo teorema // Que hay para bailar bien el rock // […]

Pero también podéis disfrutar de las versiones de Los Milos, Lolita Garrido, Los Hooligans o incluso la versión de Adriano Celentano.
Otro tema de la geometría clásica que ha sido trasladado a la música es uno de los teoremas del matemático griego Tales de Mileto (aprox. 624-546 a.n.e.). El grupo argentino Les Luthiers, conocido por sus humorísticas canciones, no solo dedica una canción, El teorema de Tales (divertimento matemático) (1971), a este resultado geométrico, sino que se atreven con mucho más, ya que en la letra incluyen el enunciado del propio teorema.
Para empezar, podemos escuchar el tema El teorema de Tales (divertimento matemático).
Como muchos temas de Les Luthiers empieza con una desternillante introducción, que dice así.
Johann Sebastian Mastropiero dedicó su divertimento matemático op. 48, el «Teorema de Thales», a la condesa Shortshot, con quien viviera un apasionado romance varias veces, en una carta en la que le dice: Condesa, nuestro amor se rige por el Teorema de Thales, cuando estamos horizontales y paralelos, las transversales de la pasión nos atraviesan y nuestros segmentos correspondientes resultan maravillosamente proporcionales.
El cuarteto vocal «Les frères luthiers» interpreta Teorema de Thales» op. 48, de Johann Sebastian Mastropiero. Son sus movimientos: Introducción, Enunciazione in tempo di menuetto, Hipotesis agitatta, Tesis, Desmostrazione, ma non troppo, Finale presto con tutti.

A continuación, viene lo que es la canción propiamente dicha, que incluye el enunciado del teorema de Tales.
Si tres o más paralelas // Si tres o más parale-le-le-las // Si tres o más paralelas // Si tres o más parale-le-le-las // Son cortadas, son cortadas // Por dos transversales, dos transversales // Son cortadas, son cortadas // Por dos transversales, dos transversales // Si tres o más parale-le-le-las // Si tres o más parale-le-le-las // Son cortadas, son cortadas (Son transversales, son transversales) // Son cortadas, son cortadas (Son transversales, son transversales) // Dos segmentos de una de éstas, dos segmentos cualesquiera // Dos segmentos de una de éstas son proporcionales // A los dos segmentos correspondientes de la otra // Hipótesis // A paralela a B // B paralela a C // A paralela a B, paralela a C, paralela a D // O-P es a P-Q // M-N es a N-T // OP es a PQ como MN es a NT // A paralela a B // B paralela a C // OP es a PQ como MN es a NT // La bisectriz yo trazaré // Y a cuatro planos intersectaré // Una igualdad yo encontraré // OP+PQ es igual a ST // Usaré la hipotenusa // Ay, no te compliques, nadie la usa // Trazaré, pues, un cateto // Yo no me meto, yo no me meto // Triángulo, tetrágono, pentágono, hexágono // Heptágono, octógono, son todos polígonos // Seno, coseno, tangente y secante // Y la cosecante y la cotangente // Thales, Thales de Mileto // Thales, Thales de Mileto // Thales, Thales de Mileto // Thales, Thales de Mileto // Que es lo que queríamos demostrar // Que es que lo que lo que queria queríamos demo demostrar.
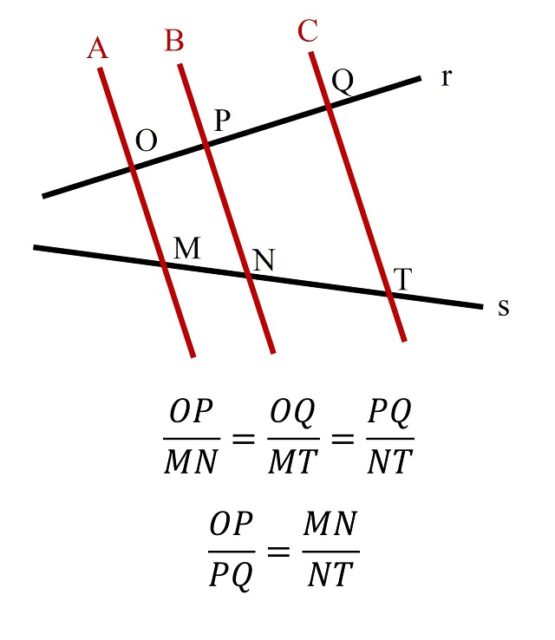
Recordemos, sin entrar en mucho detalle, que el teorema de Tales nos dice que, si dos rectas secantes r y s, que se intersecan en un cierto punto, cortan a tres rectas paralelas A, B y C, en los puntos O, P, Q y M, N, T, entonces existen relaciones de proporcionalidad entre algunos de los segmentos que se originan. Entre otras las que aparecen en la siguiente imagen, la segunda de ellas es la cantada por Les Luthiers.
También hemos dedicado alguna entrada del Cuaderno de Cultura Científica al Teorema de Tales, una versión sencilla, y aplicaciones del mismo, en concreto la entrada Tales de Mileto y el caso del gato que venía del cielo.
Después de mencionar estos dos teoremas de la geometría clásica, pasemos a un famoso teorema de la teoría de números, el último teorema de Fermat. El teorema nos dice lo siguiente.
Último teorema de Fermat: no es posible encontrar tres números enteros positivos x, y, z tales que verifiquen la ecuación, xn + yn = zn, para n mayor, o igual, que 3.
Recordemos un poco la historia de este teorema, como ya hicimos en la entrada Euler y el último teorema de Fermat. La historia del último teorema de Fermat se inicia con la edición en latín, realizada por Bachet de Méziriac, amigo del jurista francés y aficionado a las matemáticas Pierre de Fermat (1601-1665), del libro Aritmética de Diofanto. Fermat escribió en el margen de este libro, al lado del problema de expresar el cuadrado de un número como la suma de los cuadrados de dos números, es decir, buscar soluciones de números enteros positivos a la ecuación pitagórica x2 + y2 = z2 (existen infinitas soluciones, ternas pitagóricas, como (3,4,5) o (5,12,13)), lo siguiente.
“Cubum autem in duos cubos, aut quadratoquadratos, et generilater nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividiré cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exigüitas non caperet”,
es decir,
“Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración maravillosa. El margen es demasiado pequeño para que quepa en él”.
En consecuencia, el conocido como último teorema de Fermat. Sin embargo, Pierre de Fermat nunca publicó ninguno de sus resultados matemáticos. Estos se encontraban como anotaciones en los márgenes de sus libros, en particular, de los seis libros que conformaban la Aritmética de Diofanto, en sus notas manuscritas y en las cartas a otros colegas matemáticos. A su muerte, su hijo Clement-Samuel decidió recopilar y publicar todos los resultados matemáticos de su padre, para evitar que se perdieran. Por ejemplo, en 1670 publicó la obra Diophanti arithmeticorum libri cum observationibus P. de Fermat (es decir, Aritmética de Diofanto con observaciones de P. de Fermat), que contenía la versión original griega, la latina de Bachet y cuarenta y ocho observaciones del conocido como príncipe de los aficionados, una de las cuales era la anotación sobre la solución de la ecuación diofántica xn + yn = zn. Sin embargo, no se encontró ni entre sus papeles, ni en las cartas a otros matemáticos, la mencionada “maravillosa demostración”.
La historia que se inicia en el margen de la Aritmética de Diofanto termina cuando el matemático inglés Andrew Wiles demuestra finalmente, más de 350 años después, este famoso resultado matemático.
Después de darle vueltas a algunas posibilidades, entre ellas un grupo cuyo nombre es Fermat Last Theorem, me decidí por el tema Theorem, del álbum Transform (2005), del grupo de metal rock experimental de Los Ángeles (EEUU), Kineto. Un grupo algo diferente a otros grupos de metal rock, en el que el bajo se convierte en el instrumento principal, que es acompañado por unas guitarras un poco ruidosas y la batería. A este, su primer álbum, pertenece esta canción sobre el último teorema de Fermat, que podemos escuchar aquí: Theorem.
Vayamos con la letra de la canción, que nos habla del matemático inglés Andrew Wiles, de cómo estaba interesado en el teorema desde pequeño, de cómo trabajó sin descanso para demostrar el resultado de Fermat, de cómo finalmente consiguió la demostración de tan ansiada conjetura, de cómo se descubrió que había un pequeño error en la misma, de cómo Wiles se encerró para conseguir corregir el error y de cómo contó con la colaboración de su colega Richard Taylor, hasta que consiguieron corregir el error y obtener la ansiada demostración.

La letra, junto con una sencilla traducción realizada para esta entrada, dice así:
A lifetime obsession // a childhood dream // Fermat’s last theorem // led him far from the mainstream.
“Una obsesión de toda la vida, un sueño de la infancia, el último teorema de Fermat le llevó lejos de lo convencional”.
Sleepless nights // slowburn days // problems, proofs // endless delays.
“Noches en blanco, días que transcurren lentamente, problemas, demostraciones, retrasos interminables”.
Will it ever end?// Can I even stop it? // Is there a solution? // Is it really worth it?
“¿Terminará alguna vez? ¿Puedo siquiera detenerlo? ¿Existe solución? ¿Merece la pena?”
A breakthrough had come // after years of struggle // he finally put together // the pieces of the puzzle.
“Tras años de lucha había llegado un gran avance, finalmente había juntado las piezas del rompecabezas”.
His students and mentors // each gazed in awe // But little did they know // of the fatal flaw.
“Sus estudiantes y mentores miraban con asombro, pero poco sabían del fatal error”.
An error so subtle // A mistake so abstract // A decade of figures // has began to crack.
“Un error tan sutil, un error tan abstracto, una década de números ha empezado a resquebrajarse”.
A miscalculation // underneath the lens // His whole life’s work // a means to an end.
“Un error de cálculo bajo la lupa, el trabajo de toda su vida, un medio para un fin”.
His Cambridge colleague // lent a guiding mind // and repaired the flaw of // the proof that was soon to shine.
“Su colega de Cambridge le prestó una mente orientadora y repararon el defecto de la prueba que pronto iba a brillar”.
The journey is over // the achievement done // An hour of freedom before // he starts another one.
“El viaje ha terminado, el logro realizado, una hora de libertad antes de que empiece otro”.
La demostración del teorema de Fermat por parte de Andrew Wiles fue de esas raras noticias matemáticas que llegaron a los medios de comunicación de todo el mundo, incluso un libro de divulgación de las matemáticas como El enigma de Fermat (1997), de Simon Singh, se convirtió en un bestseller. Por este motivo, no es de extrañar que fuera un tema que llegó a las artes y la cultura. En el Cuaderno de Cultura Científica hemos mostrado algunos ejemplos, como en el cómic, en la entrada Las matemáticas en el cómic Ken Games, en el teatro, en Andrew Wiles: de conjetura a teorema (de Marta Macho), o en la literatura, en La chica que soñaba con una cerilla y un bidón de gasolina, por mencionar algunos ejemplos. Aunque en relación a la literatura, escribí un pequeño ensayo sobre el tema en la revista Épistémocritique, titulado Avatares literarios del Teorema de Fermat.
Existen varios temas musicales sobre el teorema de Fermat. Además de la anterior canción os animo a escuchar el siguiente tema de música electrónica. Es la canción Fermat’s theorem, perteneciente al disco Visions (1997), del DJ y productor de música electrónica británico John B (John Bryn Williams).

Si seguimos con la teoría de números, podemos hablar de otra conjetura que, contrariamente a lo que ha ocurrido con el último teorema de Fermat, no ha sido demostrada aún. Se trata de la conjetura de Goldbach.
Conjetura de Goldbach: “todo número par mayor que dos puede escribirse como suma de dos números primos”
También tenemos una entrada del Cuaderno de Cultura Científica para saber más sobre esta sencilla, pero escurridiza, conjetura. Es la entrada La conjetura de Goldbach.
En relación a la misma, vamos a escuchar el tema Goldbach conjecture de la mano de Tripswitch, un proyecto de música electrónica, del músico y productor londinense Nick Brennan (con una larga carrera en la que ha tocado muchos estilos de música diferentes: clásica, rock, blues, jazz, acid house, reagee, etc.). Tripswitch es un proyecto de música electrónica “down-tempo” con influencias sicodélicas y étnicas. El tema Goldbach conjecture pertenece al segundo álbum de Tripswitch, Geometry (2010), que incluye temas como Stereogram, Strange Parallels, Concentric Circles, etc. Aquí tenéis la canción: Goldbach conjecture.

Os dejo con otra canción sobre la conjetura de Goldbach de grupo de Bristol The Last Days, que forma parte de su disco Typography (2018): Goldbach conjecture.
A continuación, vamos con la hipótesis de Riemann, que es uno de los siete problemas del Milenio, por cuya demostración el Instituto Clay de Matemáticas ha ofrecido un millón de dólares. La hipótesis de Riemann, que debe su nombre y su formulación al matemático alemán Bernhard Riemann (1826-1866), es una conjetura sobre la distribución de los ceros de una compleja función matemática, la función zeta de Riemann. Además, la hipótesis de Riemann está relacionada con la distribución de los números primos en el conjunto de los naturales (véase Buscando lagunas de números primos).
Sobre esta cuestión he elegido un joven grupo catalán de indie-folk Plombiers, que grabó su primer EP, La darrera gènesi, en 2017, el cual incluía el tema La Hipòtesi de Riemann. Que podéis escuchar aquí.

La letra es la siguiente, con una sencilla traducción:
Mentre la pols es muda de casa // la roba s’eixuga al terrat // descripcions del dia a dia // com la hipòtesi de Riemann.
Que podría traducirse, más o menos, como “Mientras el polvo se muda de casa la ropa se seca en la azotea, descripciones del día a día como la hipótesis de Riemann”.
Les matemàtiques cassolanes // s’enamoren dels nombres prims // i mentre aquests es distribueixen // un servidor somia amb l’infinit.
Donde se menciona la distribución de los números primos: “Las matemáticas caseras se enamoran de los números primos y mientras estos se distribuyen, un servidor sueña con el infinito”.
Un punt de llibre en forma de frontera // entre allò vist i allò per descubrir // escriure versos mai va ser tan fácil // si es fa ràpid i tranquil.
Que se podría traducir (utilizando un traductor) algo así como “Un punto de libro en forma de frontera entre lo visto y lo por descubrir. Escribir versos nunca fue tan fácil si se hace rápido y tranquilo”.
Una cançó sense lletra // i una lletra sense estil // una buidor, una guerra, // una idea i un escrit.
Y de nuevo “Una canción sin letra y una letra sin estilo, un vacío, una guerra, una idea y un escrito”.
No vamos a alargar más esta entrada y vamos a despedirnos con una canción más, El teorema de Arquímedes, perteneciente al LP Matatiempo (2010), del grupo punk madrileño Desechos. La podéis escuchar aquí. La letra dice lo siguiente:
Si ves que mis pies caminan rectos, y mi cabeza está bien amueblada, y mi visión clara es, algo en tu mirada falla me has visto al revés, no te hagas líos, nadie es lo que tú crees, no cada cual, cada quien, es en parte lo que deja ver, pero flotamos en el agua como un iceberg, según supo decirnos el bueno de Arquímedes, oye su teorema y dime como lo ves. Un cuerpo sumergido en un líquido pierde parte de su peso, sufre un empuje de abajo a arriba igual al volumen del líquido que desaloja por eso flota. Quien no tropieza o mira atrás, y cuando menos se lo espera zas! cae de bruces y vigila no haber sido visto, disimula, finge de nuevo estar listo, recompone su ropa como puede y como si nada, nada a favor de la corriente y trata de alcanzar la orilla para descansar, quien no se ahoga, quien no ha sentido alguna vez que ya no puede mas, quien no ha visto en un vaso de agua el mar, quien no quiere escapar.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica