Como ya mencionamos en la entrada del Cuaderno de Cultura Científica titulada A vueltas con el origen del ajedrez, la relación entre ajedrez y matemáticas ha sido siempre muy fructífera.

Problemas clásicos como el recorrido del caballo sobre el tablero de ajedrez, el problema de Guarini (al que dedicamos la entrada Ajedrez y matemáticas: el problema de Guarini), el problema de las ocho reinas o el problema de los ocho oficiales, entre otros, fueron estudiados por grandes matemáticos como Carl F. Gauss, Leonhard Euler, Abraham de Moivre o Adrien-Marie Legendre. Así mismo, muchos matemáticos recreativos como Lewis Carroll, W. W. Rouse Ball, Henry E. Dudeney, Sam Loyd, Édouard Lucas, Raymond Smullyan o Martin Gardner, se apasionaron con este juego, incluso fueron grandes jugadores, e inventaron interesantes rompecabezas matemáticos y juegos de ingenio sobre el tablero de ajedrez.

El problema del recorrido del caballo

La entrada de hoy la vamos a dedicar a uno de esos problemas matemáticos clásicos relacionado con el tablero del ajedrez, el problema del recorrido del caballo. Aunque el juego es muy sencillo de explicar, dejemos que sea el gran matemático suizo Leonhard Euler (1707-1783), el primero en realizar un análisis matemático riguroso del juego, quien nos explique en qué consiste el mismo, con las palabras que utilizó en su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, 1759):

Un día me encontraba en una reunión en la que, con ocasión del juego del ajedrez, alguien propuso la cuestión de recorrer con un caballo todas las casillas de un tablero sin pasar nunca dos veces por la misma y empezando en una casilla dada. Se colocaban fichas, para este fin, en las sesenta y cuatro casillas del tablero, salvo en la que el caballo debía comenzar su ruta, y de cada casilla por la que pasaba el caballo, conforme a su camino, se retiraba la ficha, de manera que se trataba de retirar de esta forma todas las fichas sucesivamente. Había que evitar, pues, por un lado, que el caballo pasara por una casilla vacía y, por otro lado, había que dirigir su camino de suerte que recorriera finalmente todas las casillas.

Pero empecemos por el principio, por el movimiento del caballo en el tablero de ajedrez. Aunque es posible que la mayoría de las personas que estáis leyendo esta entrada conozcáis los movimientos de las piezas del ajedrez, lo primero es recordar cómo se mueve el caballo, ya que es la pieza central en este problema. Esta pieza realiza un salto o movimiento en forma de L –dos casillas hacia delante y una a un lado– como los que se muestran en la siguiente imagen.

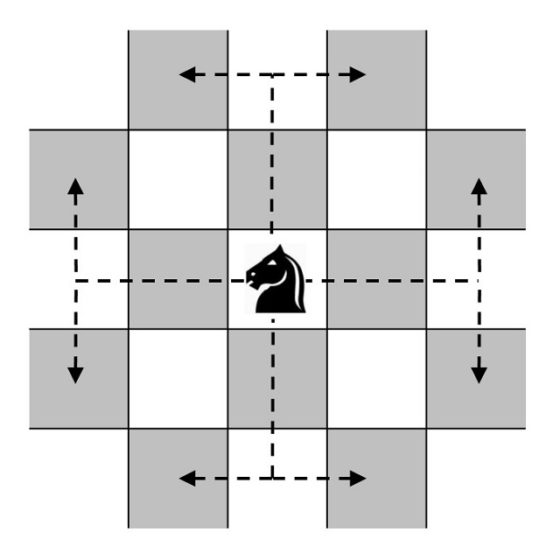
Ahora, formulemos de forma sencilla en qué consiste este juego o problema.

Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo sobre el tablero de ajedrez que consista en mover esta pieza, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas y terminando en la casilla inicial.

A un recorrido de este tipo se le denomina recorrido cerrado, ya que empieza y acaba en la misma casilla, aunque se puede plantear la variante del problema que consiste en que las casillas inicial y final no sean las mismas, en cuyo caso se habla de recorrido abierto.

Si volvemos a la explicación anterior del matemático Leonhard Euler, este no solo nos explica en qué consiste este juego, sino que además nos sugiere cómo jugarlo para que podamos comprobar si lo estamos resolviendo bien. Al ir moviendo el caballo por el tablero y quitando las fichas de las casillas por las que pasa, lo que ocurre es que si una casilla no tiene pieza quiere decir que ya la hemos recorrido y que no podemos volver a pasar por ella.

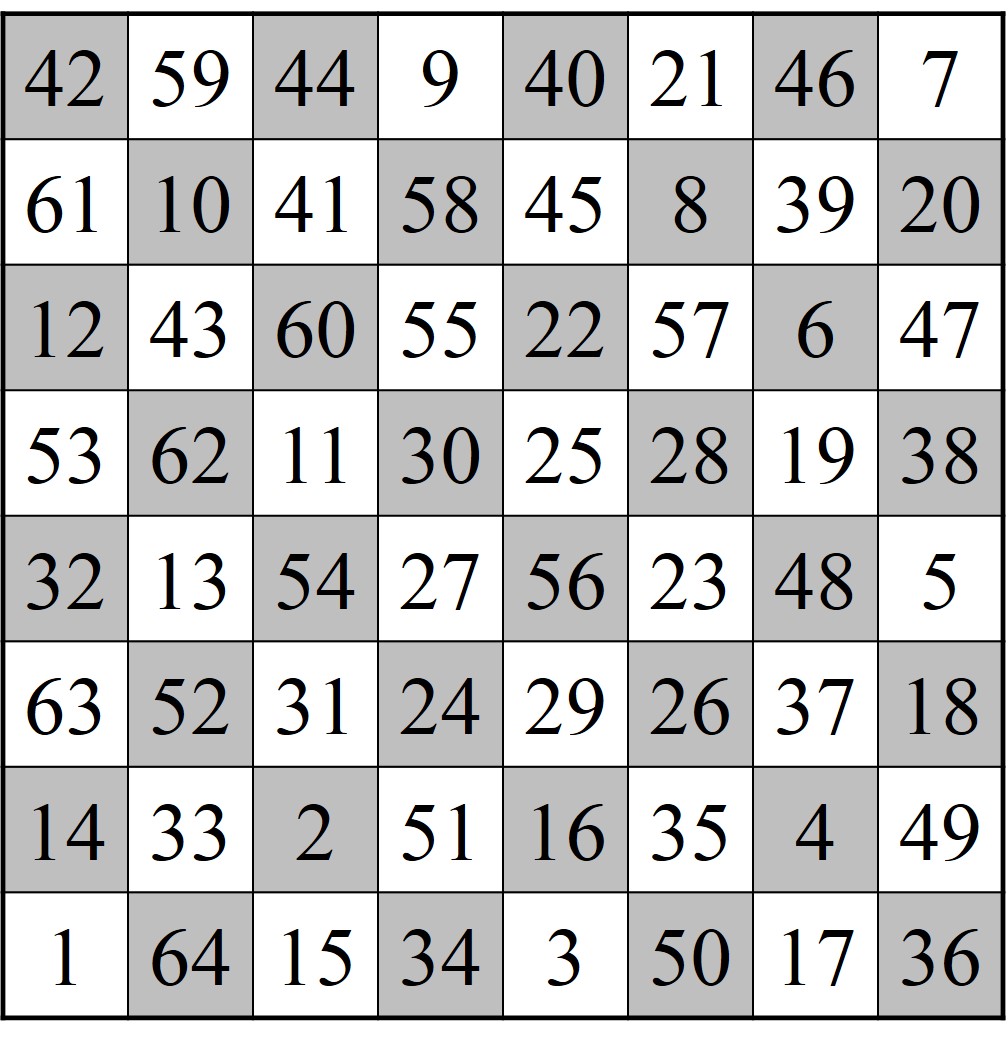
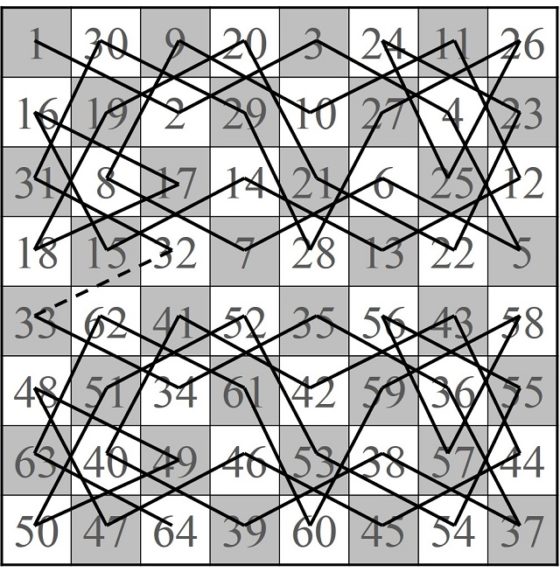
Por su parte, el matemático francés Edouard Lucas (1842-1891), autor del texto Recreaciones matemáticas (1894), propone ir colocando números del juego de la “lotería” (al parecer se refiere al bingo, ya que el origen de este juego podría estar en la lotería italiana y en Francia se conocía, en un principio, con el nombre de lotería) en las casillas recorridas, empezando por el 1 en la inicial y en orden consecutivo (1, 2, 3, 4, 5, etc), de forma que no solo sabemos si hemos recorrido todas las casillas, además una sola vez por cada una, sino que queda constancia del recorrido que se ha realizado. Esencialmente esta es la forma en la que suelen mostrarse los recorridos de los caballos. En la siguiente imagen se muestra un recorrido abierto del caballo a lo largo de todas las casillas del tablero de ajedrez (es una de las soluciones propuestas por Euler), indicado con números, como sugiere Edouard Lucas.

Origen del problema del recorrido del caballo

Como se explica en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos (RBA, 2015), este problema es mucho más antiguo. Probablemente, su origen se remonte al mismo origen del juego del ajedrez, alrededor del siglo VI en la India. Harold Murray, en su libro Historia del ajedrez, cita los manuscritos homónimos titulados Libro del ajedrez (Kitab ash-Shatranj) de los grandes ajedrecistas árabes Al-Adli (hacia el 840) y Al-Suli (hacia el 910), como los primeros en los que se presentan recorridos cerrados del caballo en el tablero clásico 8 x 8 (véase la siguiente imagen).

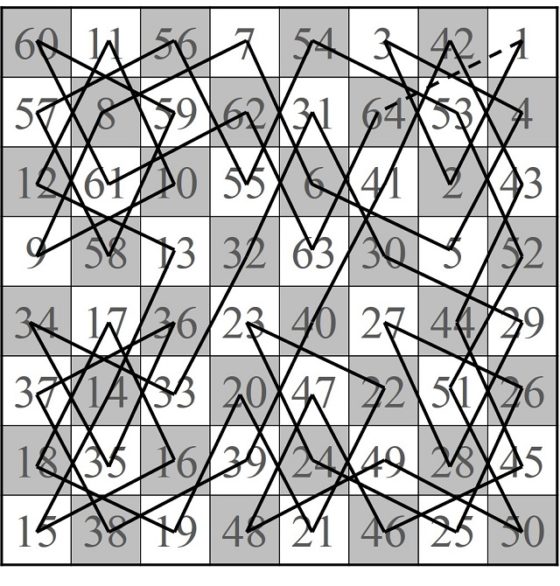
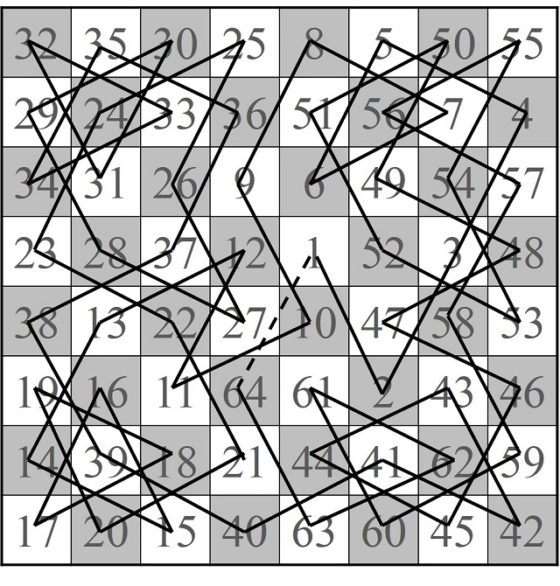
Además, el poeta de Cachemira Rudrata, en su obra poética Kavyalankara (hacia el 900), utiliza un recorrido abierto del caballo en un tablero 4 x 8 (que se puede extender a un recorrido abierto sobre un tablero de ajedrez) como una estructura para un poema. El poema, en sanscrito, se compone de cuatro líneas de 8 sílabas, que puede leerse de izquierda a derecha o siguiendo el recorrido del caballo (véase la siguiente imagen).

Al parecer, tanto en la India, como en los Países Árabes, se empezó estudiando el problema del recorrido del caballo sobre la mitad del tablero, es decir, sobre un tablero 4 x 8.

El grafo asociado al problema

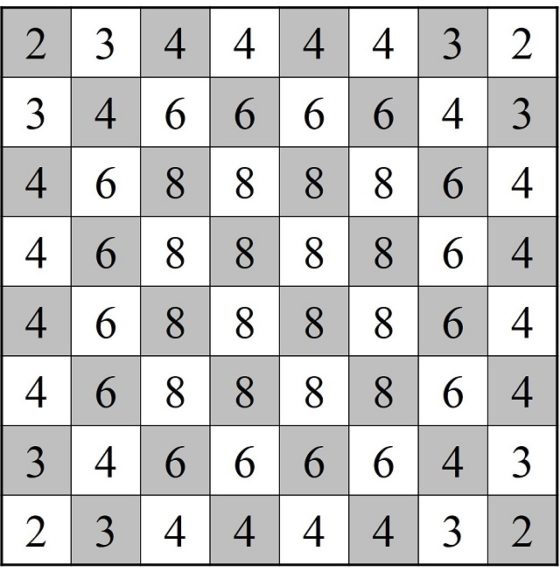
Antes de seguir adelante, vayamos con un par de comentarios. El primero es que según la posición de cada casilla esta se puede conectar, mediante el movimiento del caballo, con una cantidad distinta de casillas. En el caso de una casilla que es muy “interior”, donde todos los movimientos mostrados arriba son posibles, se puede conectar con otras ocho casillas, sin embargo, hay casillas que se pueden conectar con un menor número de casillas (dos, tres, cuatro o seis), como se muestra en la siguiente imagen.

El segundo comentario es que el problema del recorrido del caballo sobre un tablero de ajedrez se puede plantear matemáticamente como un “problema de existencia de caminos o ciclos hamiltonianos sobre un grafo”. No vamos a meternos ahora en la teoría de grafos, pero sí explicaremos cuál es el grafo asociado al problema del recorrido del caballo, ya que puede servirnos para entender algunas cuestiones más adelante.

Recordemos que un grafo está formado simplemente por puntos –llamados vértices del grafo- y líneas que unen algunos de esos puntos –llamadas aristas del grafo- (véase, por ejemplo, El problema de los tres caballeros y los tres criados, El grafo de Marion (gray) o El juego de Sim, entre otros), y que es una estructura matemática muy sencilla, pero a la vez muy versátil.

El grafo asociado al problema del recorrido del caballo es el grafo cuyos vértices son las casillas del tablero y una arista une dos vértices (casillas) si el caballo puede saltar de una casilla a la otra, con su movimiento. En la siguiente imagen hemos representado el grafo asociado.

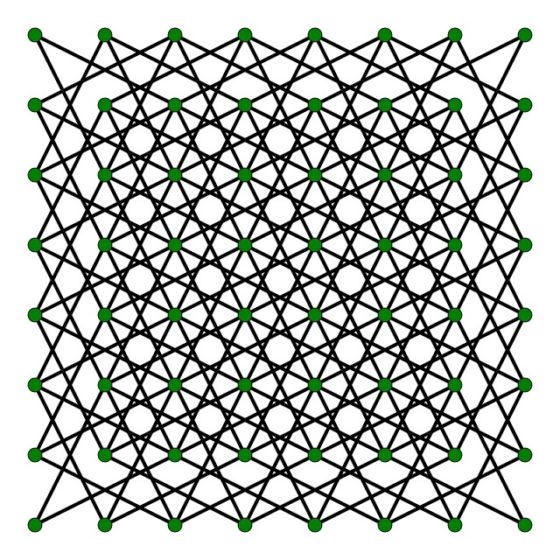
Como podemos observar, el número de aristas de cada vértice del grafo (lo que se llama el grado del vértice) es distinto, puede ser dos, tres, cuatro, seis u ocho, que son los posibles movimientos del caballo en las diferentes casillas. El problema matemático consiste en buscar un recorrido a través de las aristas que pase por todos los vértices (lo que se llama camino o ciclo hamiltoniano), aunque puede parecernos una locura ahora tiene sus ventajas, pero no entraremos en ellas ahora.

Todo un mundo de tableros

Volvamos al problema del recorrido del caballo por el tablero de ajedrez. El matemático Leonhard Euler planteó la cuestión de buscar recorridos de caballos, cerrados o abiertos, en tableros con diferentes formas, por ejemplo, rectangulares o en forma de cruz, como aparece en la imagen, y de diferentes tamaños.

Como siempre comentamos en este tipo de entradas del Cuaderno de Cultura Científica lo mejor cuando nos encontramos ante un juego es jugar. Por eso mismo, os planteo que antes de seguir adelante, o mejor después de leer esta entrada, juguéis al problema del recorrido (abierto) del caballo para estos dos tableros.

Problema: Buscar un recorrido abierto en el tablero rectangular 3 x 4 y en el tablero en forma de cruz.

Esta entrada vamos a centrar nuestra atención en los tableros cuadrados n x n (generalizando el caso del tablero clásico 8 x 8) y los tableros rectangulares n x m (generalizando el problema para la mitad del tablero, es decir, para un tablero rectangular de tamaño 4 x 8, que ya se plantearon en la antigüedad).

Un argumento de color

Es curioso que, aunque la estructura bicolor del tablero de ajedrez (cuadrados blancos y negros de forma alternada) no es relevante para resolver el problema del recorrido del caballo, sí lo es para extraer algunas conclusiones interesantes.

Si observamos el salto del caballo sobre el tablero de ajedrez bicolor nos daremos cuenta de que, si el caballo está en una casilla blanca, al moverse pasará a una casilla negra, y viceversa. Por lo tanto, en un recorrido cerrado del caballo, es decir, que tras la última casilla se regresa a la casilla inicial, el número de casillas blancas y negras deber ser el mismo. Esto nos permite afirmar que no existen recorridos cerrados en tableros n x n, para n impar, o más generalmente, en tableros rectangulares, n x m, con n y m impares, ya que el número total de casillas es impar, luego no hay la misma cantidad de casillas blancas y negras. De forma análoga, en un recorrido abierto del caballo, la diferencia en el número de casillas blancas y negras es como mucho 1, luego en tableros con formas tales que tal diferencia sea mayor que 1 no existirán recorridos del caballo, como el de la siguiente imagen, con 32 casillas negras y 25 blancas.

Los tableros de anchura 3

Una de las técnicas matemáticas a la hora de afrontar la resolución de un problema es analizar los casos más sencillos. A continuación, vamos a centrarnos en el problema del recorrido del caballo para los tableros de anchura 3, es decir, tableros rectangulares 3 x m (para m mayor o igual que 3). Podéis pensar qué es lo que ocurre con los tableros de anchura 2.

Empecemos por el tablero cuadrado 3 x 3. Este tablero es fácil de analizar. No admite recorridos del caballo puesto que la casilla central no se puede conectar, mediante el salto del caballo, con ninguna otra casilla.

Sobre el tablero 3 x 4 sí se pueden encontrar recorridos abiertos del caballo, como el que aparece en la siguiente imagen.

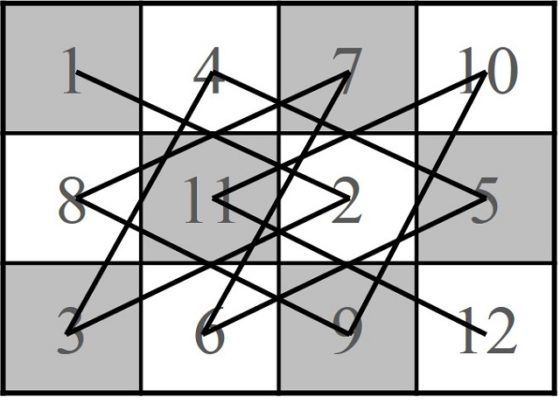
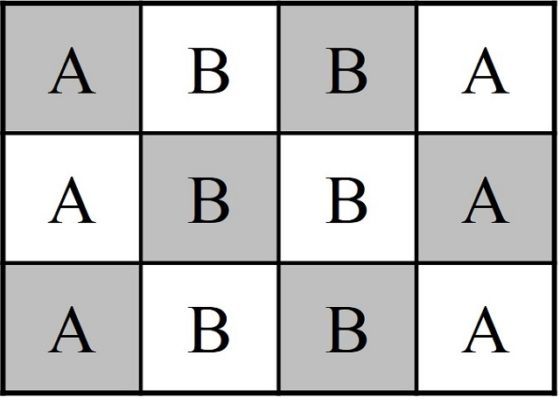
Sin embargo, no existen recorridos cerrados. Os proponemos que penséis en cómo demostrar que no existen recorridos cerrados del caballo en este tablero, aunque os daremos una pista de color (pero para no liarnos con los colores habituales del tablero, blanco y negro, utilizaremos letras, A y B), y lo resolveremos en la siguiente entrada.

Problema (recorridos cerrados sobre el tablero 3 x 4): Demostrar que no existen recorridos cerrados del caballo sobre el tablero rectangular 3 x 4.

Pista: Primero, hay que marcar la primera y la última columnas con la letra A y las dos columnas de en medio con la letra B. Y segundo, pensar a qué tipo de casilla salta el caballo si está en una casilla de tipo A, y lo mismo si está en una casilla de tipo B.

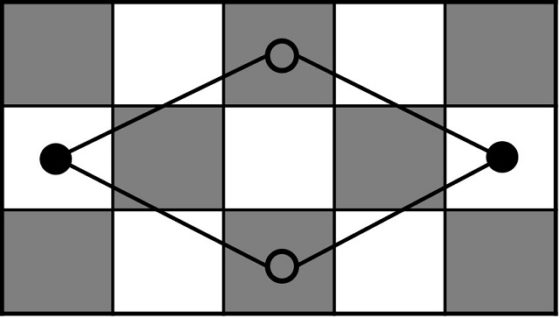
Si ahora pasamos al tablero de tamaño 3 x 5, como ambas dimensiones son impares tenemos que, por el argumento de color comentado anteriormente, no existen recorridos cerrados sobre este tablero. Pero vamos a ver que ahora tampoco existen recorridos abiertos.

En un tablero 3 x 5 coloreado como se muestra en la imagen, hay 8 casillas negras y 7 blancas, luego el recorrido del caballo deberá empezar y terminar en casillas negras. Por otra parte, si nos fijamos en las dos casillas, de la derecha y la izquierda, marcadas con los vértices negros, cada una de estas solo se puede conectar con dos casillas, que resultan ser las mismas, luego esas dos casillas marcadas con los vértices negros están conectadas a través de los dos vértices centrales, en consecuencia, necesariamente uno de los dos vértices negros deberá ser inicial o final, pero esto es imposible, puesto que son casillas blancas.

La demostración de que no existen recorridos cerrados del caballo para el tablero rectangular de tamaño 3 x 6 utiliza el grafo asociado, pero es sencilla, bonita y hace uso de una analogía con los collares de perlas, por este motivo la mostramos aquí.

Para empezar, consideremos el grafo asociado al tablero 3 x 6 (que se muestra en la siguiente imagen).

Si existiese un recorrido cerrado sobre el mismo tendremos una sucesión cerrada de aristas y vértices, luego si pensamos que los vértices son perlas y las aristas cuerdas que unen dos perlas consecutivas, podemos pensar en ese recorrido cerrado como un collar de perlas, que si lo “extendemos” (o lo “desenrollamos”) será como en la siguiente imagen (con 18 perlas).

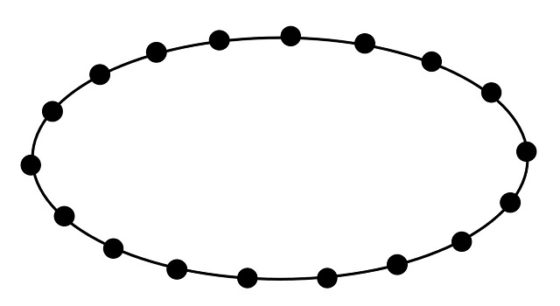
Pensemos en un collar de perlas (nos sirve la imagen anterior). Si quitamos una perla (cortando las dos cuerdas laterales) el collar estará formado por una pieza, si quitamos dos perlas quedarán dos piezas de collar, salvo que las perlas sean continuas, que quedaría una, si quitamos tres perlas, el collar se separa en tres partes como mucho, y así podemos continuar.

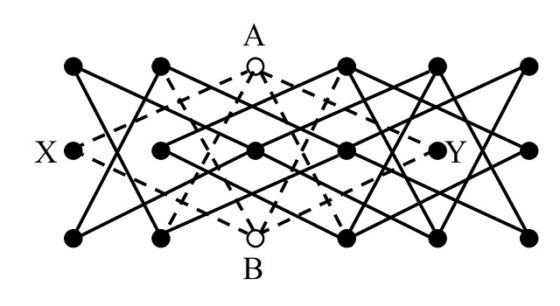
Pensemos ahora en nuestro supuesto collar de perlas, que habríamos obtenido del recorrido cerrado (si existiese) sobre el tablero 3 x 6. Ahora, si eliminamos de este collar los vértices A y B (véase la imagen anterior), quedaría dividido en tres partes, los vértices X e Y, que están aislados, y el resto de vértices, luego el collar se habría roto, al quitar A y B, al menos en tres partes, lo cual es imposible. Con argumentos similares a estos se prueba que tampoco existe un recorrido abierto.

Como hemos observado, la existencia de casillas que sólo se pueden conectar con otras dos son determinantes para demostrar que no existen recorridos (abiertos o cerrados) o para construirlos cuando sí existen. En general, se puede demostrar que no existen recorridos cerrados para los tableros 3 x m, para m impar o m = 4, 6, 8; y no existen recorridos abiertos para m = 3, 4, 5, 6.

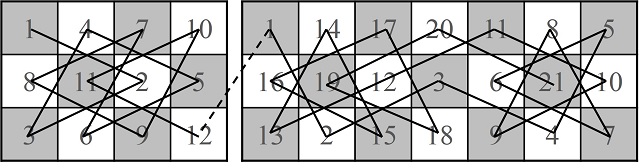
En general, uniendo tableros más pequeños se puede demostrar que existen recorridos cerrados para todos los tableros 3 x m, si m es par y mayor, o igual, que 10; y existen recorridos abiertos si m = 4 o mayor que 7. Un ejemplo de esta técnica se muestra en la siguiente imagen.

Existencia de solución al problema del recorrido del caballo

Acabamos de analizar la cuestión de la existencia de solución para el recorrido del caballo en tableros rectangulares de tamaño 3 x m. Lo siguiente podría ser analizar los tableros de tamaños 4 x m. Por ejemplo, si pensamos en un tablero 4 x 4, el argumento del collar de perlas anterior, es decir, eliminar un número de vértices y contar las partes que quedan, permite demostrar que no existen recorridos del caballo para este tablero, para lo cual hay que considerar el grafo asociado siguiente.

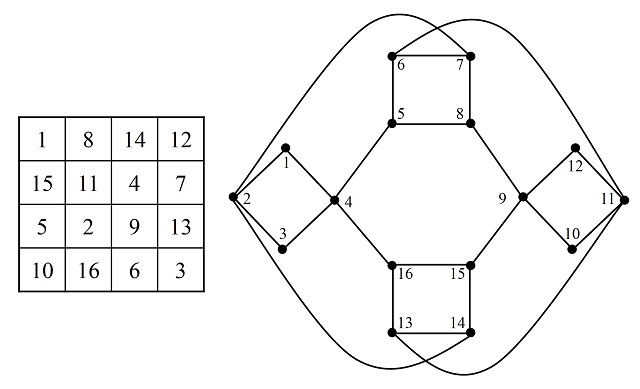
El matemático e ingeniero norteamericano Solomon W. Golomb, creador de los poliominós, dio una elegante demostración de la no existencia de recorridos de caballos cerrados para tableros 4 x m, utilizando patrones de color, pero de la existencia de recorridos abiertos (para m mayor, o igual, que 5), como puede verse en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos.

Por otra parte, los matemáticos alemanes A. Conrad, T. Hindrichs, H. Morsy y I. Wegener demostraron que existen recorridos de caballos para tableros cuadrados de lado , y que esos recorridos pueden ser cerrados para tableros pares.

Este resultado fue extendido, para recorridos cerrados, a tableros rectangulares por el matemático norteamericano Allen Schwenk, en un artículo publicado en la revista Mathematics Magazine en 1991. Para un tablero n x m, con n menor o igual que m, existen recorridos de caballos cerrados si no se da alguno de los casos anteriores: i) n y m impares; ii) n = 1, 2 o 4; iii) n = 3 y m = 4, 6 o 8.

La cuestión de la existencia de soluciones al problema del recorrido (abierto o cerrado) del caballo en tableros de ajedrez rectangulares no es el único relacionado con este problema clásico, sino que también podemos analizar otras dos cuestiones importantes, como son la construcción de soluciones al problema del recorrido del caballo o el cálculo de cuántas soluciones existen. Pero dejares estas para posteriores entradas del Cuaderno de Cultura Científica.

Bibliografía:

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.

3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.

4.- Harold J. R. Murray, A History of Chess (Historia del ajedrez), Oxford University Press, 1913.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica