El rompecabezas pitagórico
Como ya hemos expresado en más de una entrada del Cuaderno de Cultura Científica, el teorema de Pitágoras no solo es uno de los resultados más antiguos e importantes de la geometría, sino que se trata del resultado matemático más conocido y popular, que se ha convertido en un símbolo de todas las matemáticas.
Por este motivo, no es extraño encontrarnos a Pitágoras, y su teorema, en todas las manifestaciones artísticas y culturales de nuestra sociedad, como hemos recogido en algunas entradas. Así, en las entradas Cultura pitagórica: arte y El teorema de Pitágoras en el arte se muestra su presencia en pinturas y esculturas contemporáneas (véase también el libro Las matemáticas como herramienta de creación artística (R. Ibáñez, Catarata, 2023)), en la entrada Sin Noticias de Pitágoras (Pitágoras en la Literatura) se realiza un pequeño paseo por algunos ejemplos de la presencia del teorema del triángulo rectángulo en la literatura, o entre los ejemplos de canciones en las que se mencionan diferentes elementos de las matemáticas, de la entrada El teorema musical , está, como no, el resultado de Pitágoras, por mencionar algunos ejemplos.

En esta entrada vamos a relacionar este teorema geométrico griego con la matemática recreativa. En concreto, vamos a presentar el rompecabezas pitagórico.
El teorema de Pitágoras
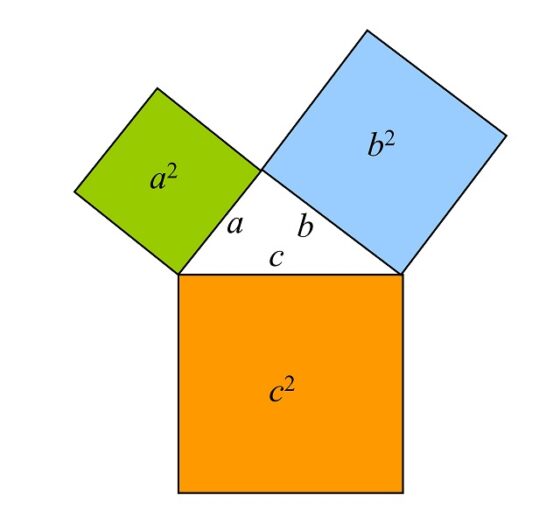
El teorema del triángulo rectángulo, que lleva el nombre del gran filósofo y matemático griego Pitágoras (ca. 569-500 a.n.e.), dice así: “dado un triángulo rectángulo, entonces el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos”, la famosa expresión algebraica a2 + b2 = c2, siendo a y b los catetos y c la hipotenusa del triángulo rectángulo. De hecho, el teorema dice algo más, también es cierto el recíproco, es decir, que “dado un triángulo para el cual el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos, entonces el triángulo es rectángulo”.
Para quienes estéis interesados en saber más sobre Pitágoras podéis leer las entradas El asesinato de Pitágoras, historia y matemáticas (I) [] y El asesinato de Pitágoras, historia y matemáticas (II), que escribí en relación con la novela El asesinato de Pitágoras (Duomo editorial, 2013), del escritor Marcos Chicot.
Como ya contamos en la entrada Pitágoras sin palabras este teorema ha sido atribuido según diferentes fuentes de la propia Grecia (los historiadores Plutarco, Diógenes Laercio, el escritor Ateneo y el filósofo Proclo) a Pitágoras, como ha trascendido hasta nuestros días. Sin embargo, existen evidencias de que era conocido por antiguas civilizaciones como en Babilonia, Egipto, India o China. Por lo que se sabe, estas civilizaciones conocían y manejaban triángulos concretos que verificaban el teorema (por ejemplo, el triángulo de lados (3, 4, 5) es un triángulo rectángulo para el que 9 + 16 = 25, conocido como triángulo egipcio), pero le debemos a Pitágoras el teorema en toda su generalidad –para todos los triángulos rectángulos y para todas las ternas de números verificando la propiedad- (es decir, hay un paso de lo concreto a lo general) y también su “demostración”, sabemos que algo “es verdad” porque se ha demostrado matemáticamente, y así ocurre con el Teorema de Pitágoras.
Demostración geométrica del teorema
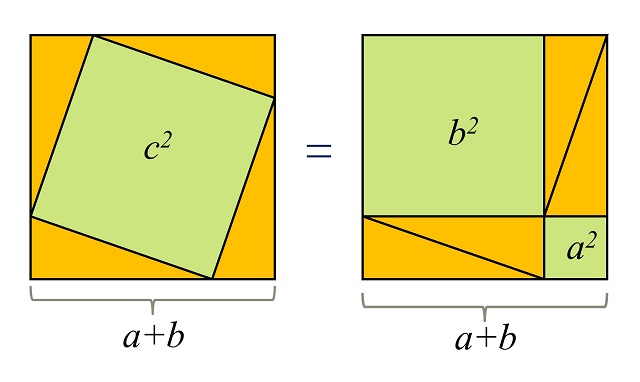
Se ha asociado siempre la demostración original de Pitágoras con una demostración geométrica-visual basada en una serie de figuras geométricas móviles, que consisten en cuatro copias del triángulo rectángulo y dos cuadrados de lado igual a los catetos del triángulo (véase la siguiente imagen).
Sin embargo, muchos historiadores son de la opinión de que la demostración se basaría en su propia teoría de las proporciones. En el libro Pitágoras, el filósofo del número, Pedro Miguel Urbaneja, Nivola, 2001, pueden verse dos posibles demostraciones según los historiadores.
Existen muchas más demostraciones del Teorema de Pitágoras, algunas de ellas de tipo geométrico-visual, como las mostradas en la entrada Pitágoras sin palabras o las que pueden verse en alguno de los libros de la serie Proofs Without Words / Demostraciones sin palabras, del matemático estadounidense Roger B. Nelsen.
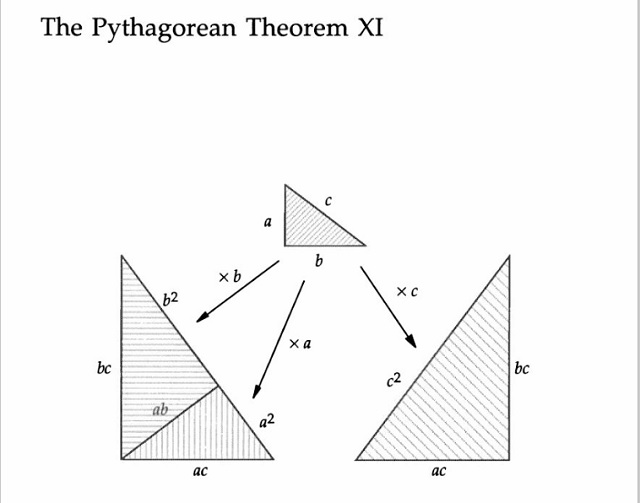
Sin embargo, nuestro objetivo en esta entrada del Cuaderno de Cultura Científica no son las demostraciones de tipo geométrico-visual, solo estamos interesados en la primera demostración que hemos mostrado, la atribuida al fundador de la hermandad de los pitagóricos, puesto que de ella deriva el rompecabezas que vamos a explicar a continuación.
El rompecabezas pitagórico
El rompecabezas que os voy a presentar, lo descubrí en el libro What’s Happening in the Mathematical Sciences 1998-1999 / Qué está pasando en las ciencias matemáticas 1998-1999, en un artículo del matemático, programador informático y diseñador de juegos de ingenio estadounidense Harry L. Nelson (1932), que fue editor de la revista Journal of Recreational Mathematics y creó la empresa MiniMax Game (sobre uno de sus juegos, Pohaku, podéis leer en la entrada El rompecabezas de los cuatro cubos de Nelson).
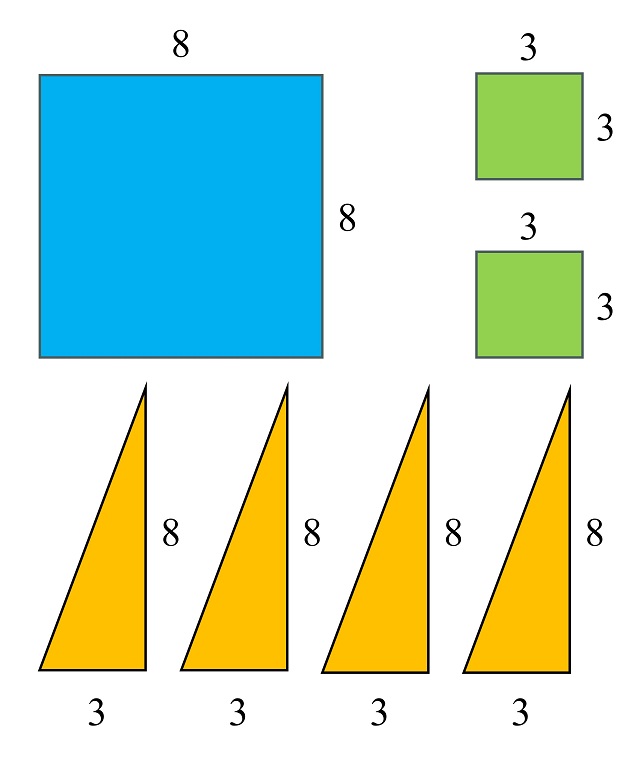
Este rompecabezas está inspirado en la demostración geométrico-visual del Teorema de Pitágoras. Las piezas del mismo, que se muestran en la siguiente imagen, son un cuadrado cuyo lado mide 8 unidades (por ejemplo, centímetros o decímetros), un cuadrado cuyo lado mide 3 unidades y cuatro copias de un triángulo rectángulo, cuyos catetos miden 8 y 3 unidades.
El tablero es un cuadrado de 15 unidades de lado sobre el que se colocan las seis piezas, como se indica en la siguiente imagen, es decir, representando la parte de la derecha de la demostración geométrica-visual, atribuida a Pitágoras, del teorema que lleva su nombre.
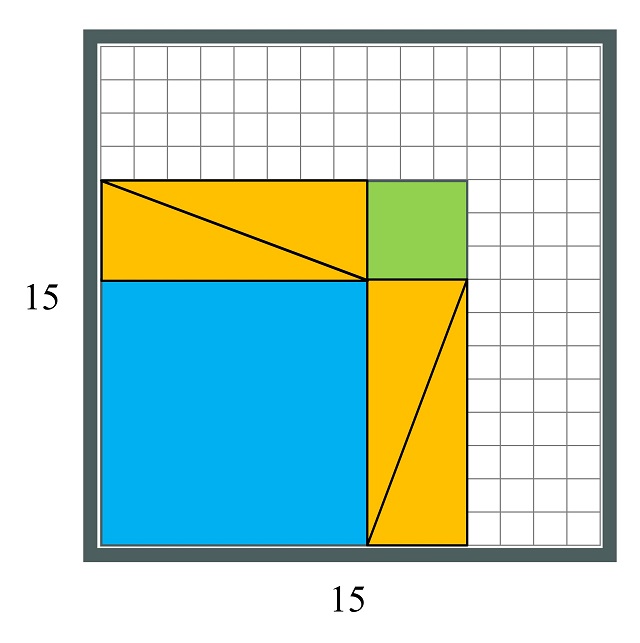
El objetivo del rompecabezas es mover, deslizando y sin levantar, las piezas del rompecabezas, pasando de la posición inicial a la posición final, que se muestra en la siguiente imagen, y que está relacionada con la otra imagen de la demostración.
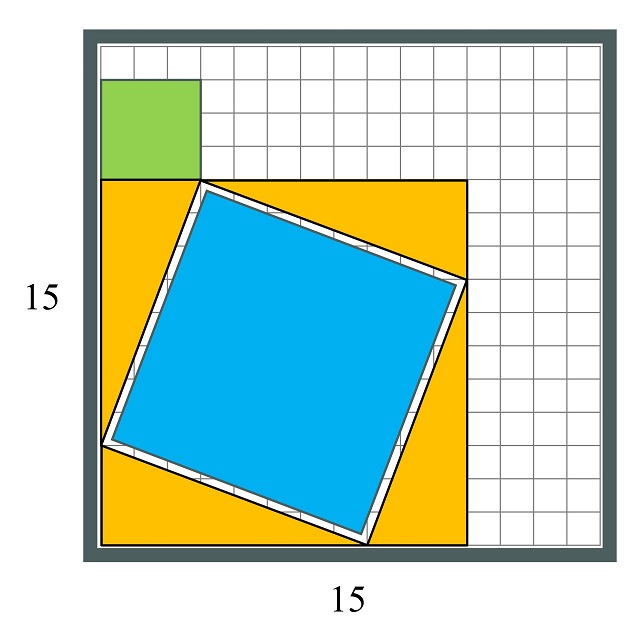
Para poder jugar a este rompecabezas lo mejor es que construyáis vosotros mismos las piezas y el tablero del juego, ya sea una versión sencilla con cartulina o cartón, o una versión en madera, que será más propicia para jugar.
Variaciones
El rompecabezas pitagórico se puede complicar un poco si vamos reduciendo el espacio de movimiento, el tablero sobre el que se deslizan las fichas.
La primera variación sería utilizar un tablero de tamaño 14 x 15, es decir, se elimina una de las columnas.
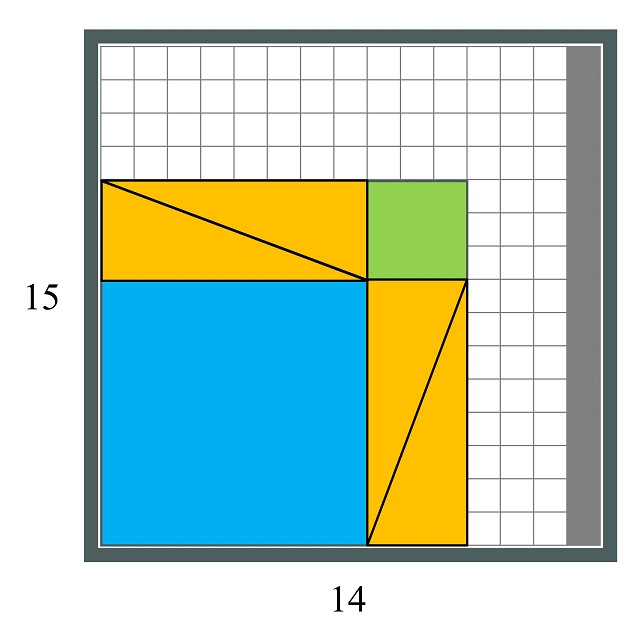
Para la segunda variación se elimina otra de las columnas, quedando un tablero de tamaño 13 x 15, por lo tanto, con menos espacio para deslizar las piezas.
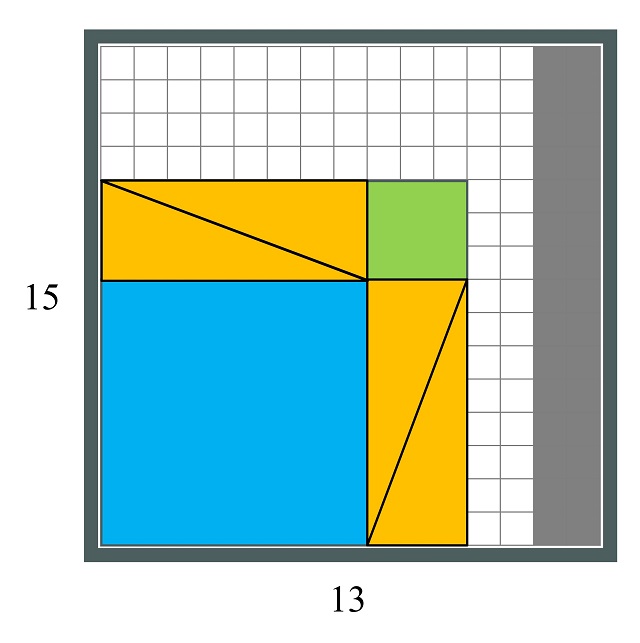
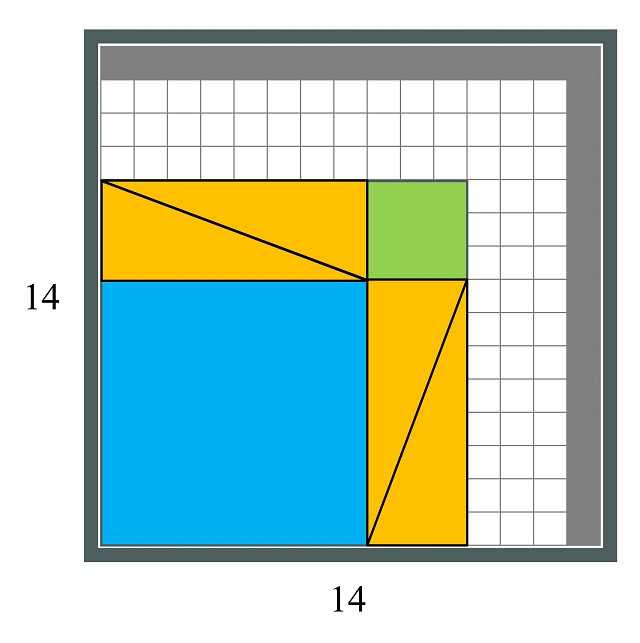
Y la tercera, y última, variación consistiría en eliminar tanto una fila, como una columna, del tablero original, quedando un tablero de tamaño 14 x 14.
Ahora es vuestro turno, construid el rompecabezas pitagórico y disfrutad jugando con el mismo.

Bibliografía:
1.- Barry Cipra, What’s Happening in the Mathematical Sciences 1998-1999, volume 4, AMS, 1999.
2.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.
3.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica