Cualquier persona que haya leído mi último libro Las matemáticas como herramienta de creación artística (2023), se habrá dado cuenta de la admiración que siento por el trabajo artístico del diseñador, artista polifacético y educador suizo Max Bill (1908-1994), figura central de arte concreto y, en mi opinión, uno de los artistas claves en el arte del siglo xx. Las matemáticas fueron fundamentales para este artista, como dejó recogido en su ensayo El pensamiento matemático del arte de nuestro tiempo (1949) y en el que se pueden leer reflexiones como la siguiente:

Creo que es posible desarrollar ampliamente un arte basado en el pensamiento matemático. Contra esta opinión se plantearon enseguida fuertes objeciones. Se afirma que el arte nada tiene que ver con las matemáticas, y que éstas son una materia árida, no artística, una cuestión puramente intelectual, que es contraria al arte. Para el arte, sólo el sentimiento es importante y el pensamiento es perjudicial. Ninguno de los dos puntos de vista es correcto, porque el arte necesita por igual del sentimiento y del pensamiento.

En el mencionado texto, Las matemáticas como herramienta de creación artística, se puede descubrir la importancia que tuvo el teorema de Pitágoras en su obra, herramienta matemática que utilizó desde, al menos, 1937, año de creación de su obra Construcción con la fórmula a² +b² = c², y que no abandonaría nunca (véase también la entrada El teorema de Pitágoras en el arte); o la profunda relación que tuvo con la banda de Moebius, desde que la redescubriera y bautizara como la cinta sin fin en 1935 (véase también la entrada Arte Moebius (I)). Pero nos podemos encontrar muchas más matemáticas en su trabajo: figuras geométricas planas –polígonos, círculos y otras curvas- y espaciales –esferas y poliedros-, el hipercubo, diferentes sucesiones de números o la combinatoria, entre otras.

En esta entrada quiero que disfrutemos, y analicemos juntos, mirando con ojos matemáticos, una hermosa serie de obras relacionada con la geometría, la combinatoria y el álgebra, su serie 11 x 4 : 4 (1963/1970).

¿Qué vemos cuando miramos?

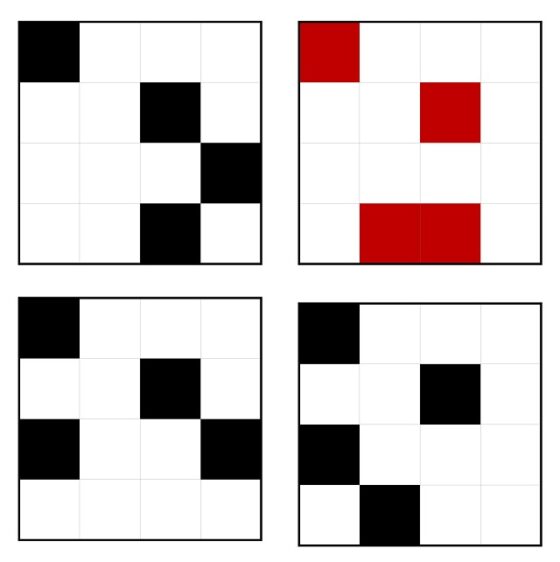
Antes de nada, analicemos esta serie de obras. Si tomamos una cualquiera de ellas, por ejemplo, la última, de la cual he realizado la siguiente reconstrucción, descubriremos algunas cosas interesantes. Para empezar, algo básico, la obra está compuesta por una retícula cuadrada de tamaño 4 x 4, es decir, con 16 pequeños cuadrados. Además, cada uno de los 16 cuadrados están coloreados con uno de los cuatro colores que se han utilizado en cada pieza, en la serigrafía de la siguiente imagen azul, rojo, amarillo y verde.

Si la descomponemos por colores, observaremos que está formada (como se muestra en la siguiente imagen) por cuatro estructuras básicas, que son la misma, salvo rotaciones de 90, 180 y 270 grados. Es decir, si tomamos la primera (la azul) podemos obtener las demás girando, en el sentido contrario a las agujas del reloj, 90 grados (verde), 180 grados (amarilla) y 270 grados (roja).

Consideremos otra de las once serigrafías que componen esta serie y veamos que ocurre lo mismo que en la anterior.

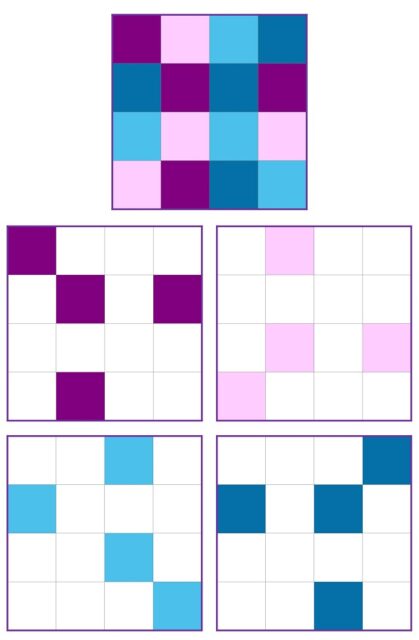
Si llamamos “patrón básico” a la estructura formada por las cuatro casillas que llevan un mismo color y de manera que una de ellas sea el vértice superior izquierdo, que en el primer ejemplo son las cuatro casillas azules y en el segundo las cuatro casillas violetas, está claro que estas obras se forman tomando el patrón básico de un color y cada rotación del patrón básico, de 90, 180 y 270 grados, con otro color distinto cada una.

Pero cuidado, no vale cualquier elección de cuatro casillas de la retícula 4 x 4, puesto que puede ocurrir que la girar, 90, 180 y 270 grados, la estructura básica haya casillas que se superponen o casillas que no estarían ocupadas, que no tendrían color, como ocurre en el siguiente ejemplo (para el que hemos elegido los mismos colores que la primera serigrafía).

Si observamos el candidato a patrón básico (azul) y sus giros en el sentido contrario a las agujas del reloj (verde, amarillo y rojo), podemos observar que hay cuatro casillas de los lados de la retícula que no quedarían cubiertas, no podríamos asignarles color según lo establecido, en concreto la tercera de la primera fila, la primera de la segunda fila, la cuarta de la tercera y la segunda de la cuarta. Y, además, las cuatro casillas del centro tendrían dos colores asignados cada una de ellas, las dos casillas centrales de la diagonal descendente tendrían asignados los colores azul y amarillo, mientras que las dos casillas centrales de la diagonal ascendente tendrían asignados los colores verde y rojo. En consecuencia, este candidato a patrón básico no sirve para generar una obra del estilo de las serigrafías de la serie de Max Bill.

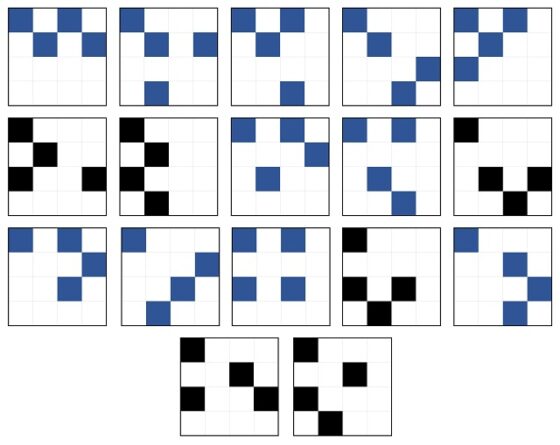
Pero volvamos de nuevo a la serie 11 x 4 : 4 y representemos los once patrones básicos asociados a las once serigrafías de la misma.

Entonces, podemos observar más cosas, además del análisis anterior de que los cuatro cuadrados del patrón básico, junto a los cuadrados de cada una de las estructuras (4 cuadrados por estructura) que consisten en girar 90, 180 y 270 grados el patrón básico, llenan la retícula 4 x 4, como que los cuadrados del patrón básico (luego los cuadrados de un mismo color en cada serigrafía de la serie) o no se tocan o se tocan solo en un vértice, nunca comparten un lado entero.

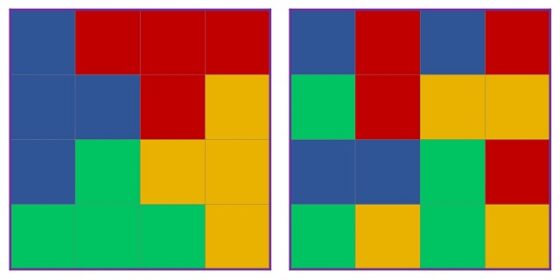
Por ejemplo, ninguno de las dos creaciones siguientes que verifica la condición de ser cuatro estructuras de cuatro cuadrados, tal que cada una se relaciona con las otras mediante giros de 90, 180 y 270 grados, y que las cuatro juntas rellenan la retícula 4 x 4, podrían formar parte de la serie de Max Bill, ya que hay cuadrados del mismo color que se tocan en un lado.

¿Y si pensamos matemáticamente?

Entre las notas de Max Bill puede encontrarse una explicación (siguiente imagen) de cómo ha generado cada una de las once estructuras básicas (patrones básicos). En este apartado intentaremos explicar el motivo por el cual considera exactamente esos once patrones básicos para generar las obras de la serie. En su explicación gráfica, empieza con una estructura básica y desplaza uno de los cuatro cuadrados de la misma para obtener una nueva estructura básica, y así hasta el final. Por ejemplo, en su primera estructura básica (que es la primera de la segunda fila de la anterior imagen de las once estructuras básicas) desplaza el cuadrado de la tercera fila y cuarta columna, al cuadrado de la primera fila y tercera columna. Debemos percatarnos que al mover ese cuadrado solo tiene tres opciones para moverlo, ya que al girar tiene que cubrir los mismos cuatro huecos (casillas) que cubría el cuadrado que ha movido. Esto nos lleva a una pequeña reflexión matemática relacionada con este proceso creativo, lo que en matemáticas se denomina la “acción de un grupo sobre un conjunto”.

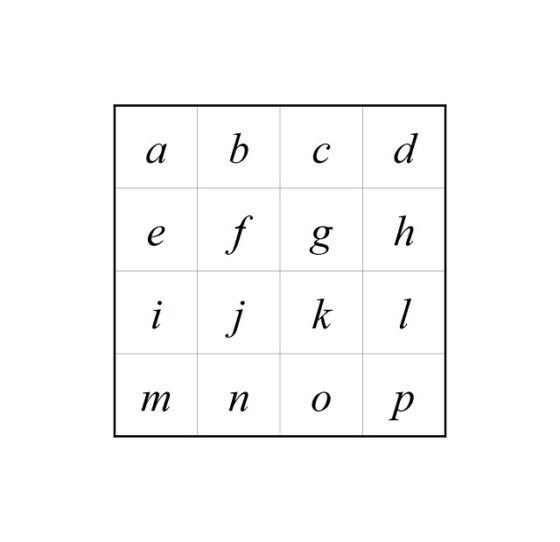
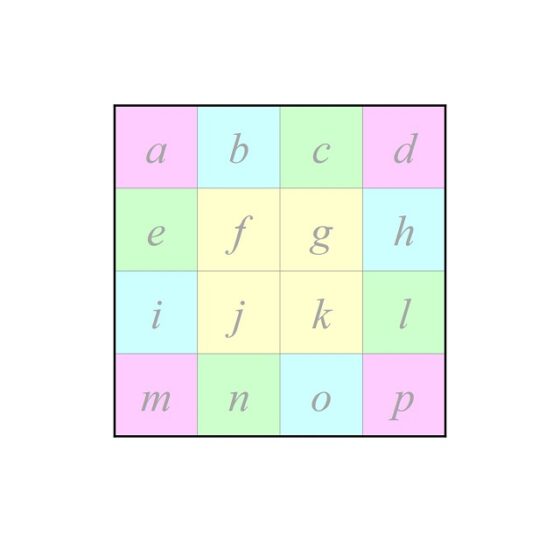
En este proceso creativo de Max Bill interviene un grupo algebraico, el grupo G de las rotaciones de un cuadrado que lo dejan invariante, que está formado por los giros de 0 grados (este giro es la identidad, no mover el cuadrado), 90 grados, 180 grados y 270 grados. En las entradas Cuadrados latinos, matemáticas y arte abstracto y La teoría de grupos en el arte contemporáneo: John Ernest se puede leer sobre la estructura algebraica de grupo, pero realmente no es necesario para entender esta entrada, cuya lectura podéis continuar sin necesidad de saber nada más que estamos trabajando con el grupo de rotaciones de un cuadrado, es decir, rotaciones de 0, 90, 180 y 270 grados. Además, se está considerando, de forma implícita, lo que se denomina la acción de un grupo sobre un conjunto. En este caso, el conjunto X estaría formado por las 16 casillas de la retícula, que en la siguiente imagen hemos nombrado con letras, de la a a la p, para entender mejor la acción del grupo.

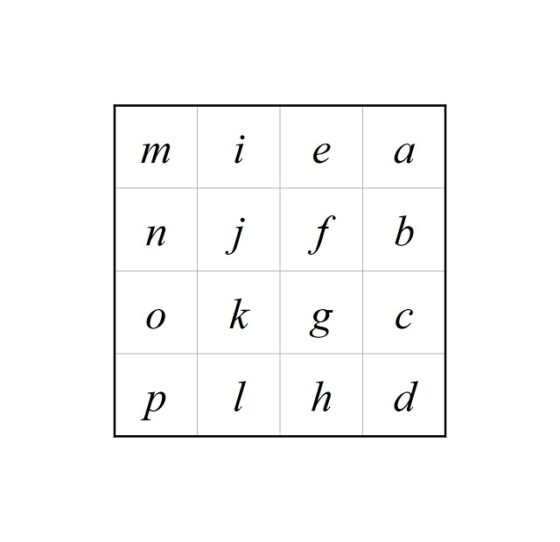
Una acción de un grupo G sobre un conjunto X consiste en una aplicación que a cada elemento del grupo g (de G) y cada elemento del conjunto x (de X) se les asocia otro elemento del conjunto X, que denotamos gx, o g(x), que consiste en aplicar g sobre x. Por ejemplo, si g es el giro de 90 grados y x es la casilla a, entonces g(x) es la casilla d, o si g es el giro de 270 grados y x es la casilla j, entonces g(x) es la casilla f (la que se obtiene al girar 270 grados en el sentido contrario a las agujas del reloj). Más aún, si tomamos g = giro de 90 grados, podemos ver en la siguiente imagen cómo se moverían todas las casillas.

El proceso creativo de Max Bill está relacionado con lo que en matemáticas se llama las órbitas de una acción de un grupo sobre un conjunto. Dado un punto cualquiera x del conjunto X, se llama “órbita de x”, a todos los elementos del conjunto que se obtienen al aplicar los elementos del grupo G sobre ese elemento x. Escrito de forma matemática, la órbita de un elemento x sería el subconjunto {g(x): para todo g de G}. Por ejemplo, en nuestro caso, si tomamos la casilla a, resulta que al aplicarle los elementos del grupo (rotaciones de 0, 90, 180 y 270 grados) se obtienen las casillas {a, d, p, m} (las casillas de las esquinas). En total, en la acción que hemos descrito, relacionada con la serie artística de Max Bill, existen cuatro órbitas, la descrita antes y otras tres, todas ellas descritas en la siguiente imagen, en la que cada color describe los elementos de una misma órbita: {a, d, p, m} (rosa), {b, h, o, i} (azul claro), {c, l, n, e} (verde claro) y {f, g, j, k} (amarillo).

¿Cómo se relaciona esto con el proceso creativo de Max Bill? Cada uno de los patrones básicos está formado por un cuadrado de cada una de las cuatro órbitas, como podéis comprobar en los once patrones básicos que hemos descrito más arriba. Por lo tanto, para crear los patrones básicos para obras de la serie de Max Bill hay que coger, para cada patrón básico, un cuadrado de cada órbita, pero con algunas condiciones que iremos explicando paso a paso.

Para empezar, de cada órbita tenemos 4 posibles cuadrados, luego existen 4 x 4 x 4 x 4 = 256 formas distintas de elegir un cuadrado de cada órbita, que son muchas formas para empezar. Como cada patrón básico, girado 90, 180 y 270 grados forma una obra de la serie de Max Bill, hay candidatos a patrones básicos de los 256 anteriores que darían lugar a la misma obra. Por ejemplo, en la siguiente imagen vemos cuatro de estos posibles patrones básicos, pero que dan lugar a la misma obra, ya que son iguales, salvo una rotación, de 90, 180 o 270 grados.

Luego de esos cuatro elegiríamos solo uno, por ejemplo, el que tiene el cuadrado de la esquina superior izquierda. Este es el motivo por el cual más arriba pusimos la condición de que un patrón básico tenga el cuadrado de la esquina superior izquierda. En consecuencia, de los 256 candidatos a patrones básicos, nos quedaremos con 256 / 4 = 64, los que tienen el cuadrado de la esquina superior izquierda, los demás son iguales a estos salvo rotación.

Es decir, de la órbita de las casillas de las esquinas, tenemos fijada la asignación de la esquina superior izquierda, y es la elección de un cuadrado en cada una de las otras tres órbitas lo que nos genera los 64 candidatos a patrones básicos. Pero no todos estos candidatos son válidos. Como comentamos más arriba, los cuadrados elegidos no se pueden tocar lado con lado, luego hay que eliminar los candidatos a patrones básicos que, como los de la siguiente imagen, tengan cuadrados que comparten un lado.

Ya tenemos documentadas las dos condiciones sobre los patrones básicos que habíamos observado en el apartado anterior, que la estructura básica rellene la retícula 4 x 4, mediante los giros de 90, 180 y 270 grados, y que no haya dos cuadrados que se toquen a través de un lado. Llegados hasta aquí, tenemos un problema de combinatoria:

¿cuántos patrones básicos existen?

Vamos a computar la cantidad de patrones, y describirlos, viendo las opciones que existen para los cuadrados de las otras tres órbitas. El primer cuadrado del patrón ya está fijado, en la esquina superior izquierda y el segundo cuadrado lo vamos a elegir de la órbita de los cuatro cuadrados centrales. Hay cuatro opciones para ese segundo cuadrado, puesto que no hay opción a que en alguna de las cuatro opciones tenga un lado en común con el cuadrado de la esquina, que son las que aparecen en la siguiente imagen.

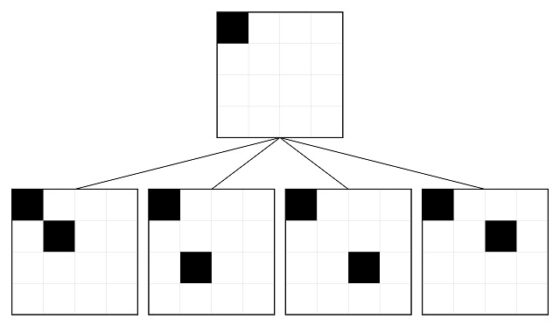
Ahora, para cada una de esas cuatro opciones, vamos a ver dónde pueden colocarse los dos cuadrados que se corresponden con las otras dos órbitas. La primera de las cuatro opciones anteriores, la de la izquierda, que tiene los dos cuadrados que se tocan por un vértice, es diferente a las otras tres, por lo que vamos a analizarla primero. Para esa primera opción cada uno de los otros dos cuadrados tienen tres opciones cada uno, solo la opción en la que comparten lado con los otros dos cuadrados no es válida. Por lo tanto, de aquí se deducen 3 x 3 = 9 patrones básicos distintos, aunque hay que eliminar dos de ellos, puesto que coinciden los cuadrados en un mismo lateral de la retícula y se tocan en un lado, quedando solo 7 patrones básicos, que se muestran a continuación (los 7 negros, ya que hemos eliminado los dos rojos).

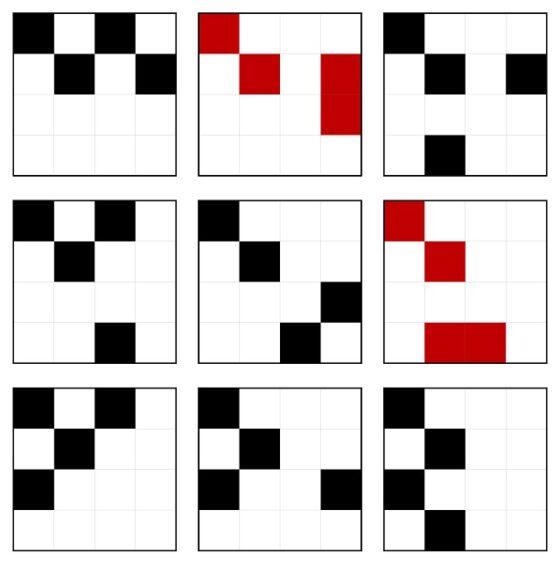
Para cada una de las otras tres opciones, cada uno de los otros dos cuadrados tienen dos opciones cada uno, luego cuatro patrones básicos para cada opción. Sin embargo, en dos de ellas dos de los cuadrados coinciden en uno de los lados, luego comparten lado, por lo tanto, en total son 10 estructuras más.

Para la primera opción …

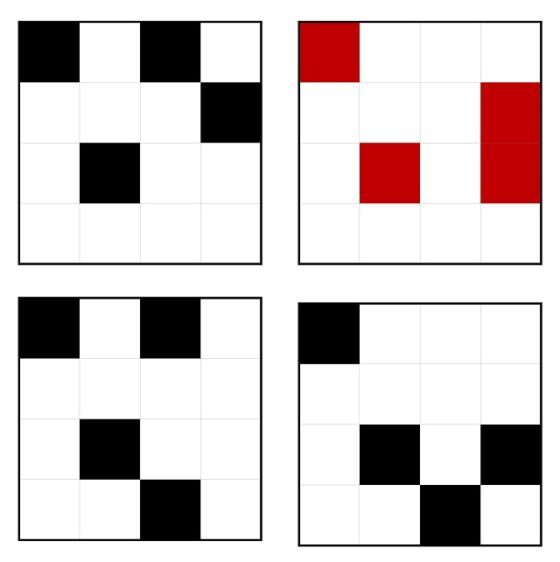
Para la segunda opción …

Y para la tercera opción …

Por lo tanto, en total son 17 patrones básicos distintos. A continuación, los mostramos todos juntos, marcando en azul los correspondientes patrones de las 11 serigrafías de la serie 11 x 4 : 4 de Max Bill. Por lo tanto, existen 6 patrones básicos que no estarían, a priori, considerados por Max Bill, aunque veremos que esto no es así.

En la explicación de Max Bill sobre el proceso creativo, que hemos incluido más arriba, el artista concreto comenta “se han excluido cinco variantes por la inversión de los grupos II, III, IV, V y XI”. Lo que ocurre es que Max Bill ha añadido, además, otra forma, intuitiva y geométrica, de establecer que dos patrones básicos son el mismo. Expliquémosla.

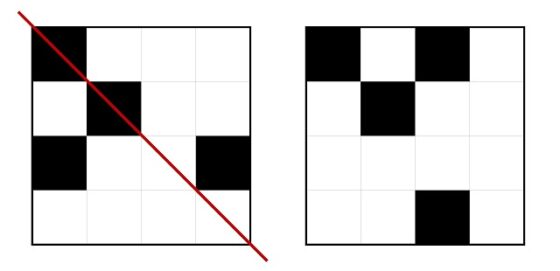
Tomemos el primero de los patrones básicos de la clasificación anterior, que no está en la lista de las 11 estructuras básicas de Max Bill, el patrón que está en la segunda fila, primera columna. Imaginemos que es una estructura tridimensional, formada por pequeños cuadrados que tienen el mismo color, blanco o negro, en la cara superior y en la cara inferior, si diésemos la vuelta (por eso Max Bill habla de “inversión”) a nuestra retícula 4 x 4 tridimensional (cuyo resultado es el mismo que tomar la imagen especular respecto a la diagonal principal descendente) nos quedaría un patrón básico, imagen especular / inversión del anterior, como se muestra en la siguiente imagen, y podríamos considerar que son la misma estructura esencialmente (ya que una es simétrica de la otra). Y ese patrón básico al que es simétrico (el de la derecha de la imagen), sí está en el listado de los patrones básicos de Max Bill, véase más arriba, es el patrón II del documento del propio artista.

Veamos que los demás patrones básicos que, a priori, no estaban en la clasificación de Max Bill, son simétricos a alguno de los que sí está en la clasificación. Tomemos el patrón que está en la segunda fila y quinta columna, resulta que es simétrico (es como voltearlo) al patrón XI de Max Bill (véase la siguiente imagen).

Ahora vamos a considerar otro patrón básico que no estaba, el que está en la tercera fila y cuarta columna. Resulta ser simétrico, como se observa en la siguiente imagen, al patrón V de la clasificación de Max Bill.

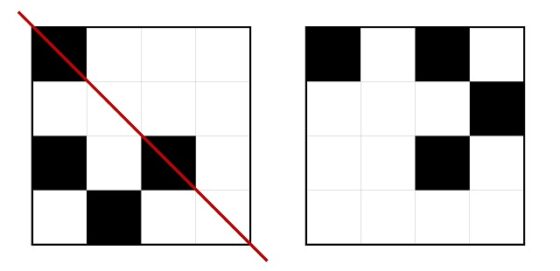
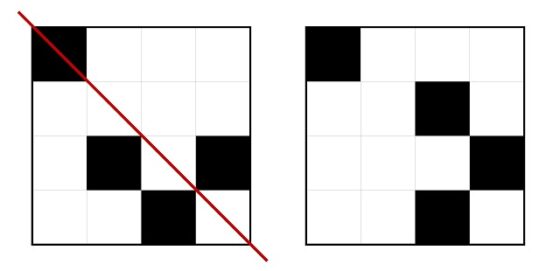
El siguiente patrón básico a considerar es el que está es el primero de la cuarta fila, que resulta ser, como se muestra en la siguiente imagen, simétrico al patrón básico III de Max Bill.

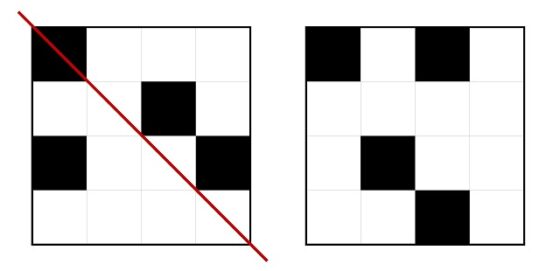
Mientras que el segundo patrón básico de la cuarta fila es simétrico, como se muestra en la siguiente imagen, al patrón IV de Max Bill.

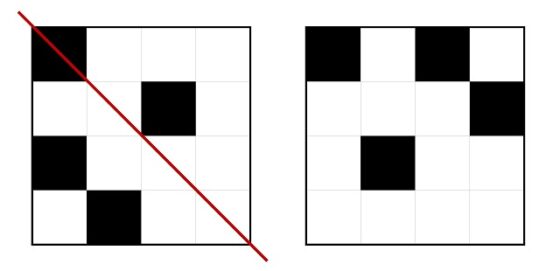
Y ahí tenemos las “inversiones de los grupos II, III, IV, V y XI” a las que alude el artista suizo y que aquí hemos denominado patrones simétricos respecto a los patrones (II, III, IV, V y XI) de la clasificación de Max Bill. Pero resulta que nos falta una estructura básica que no tuvo en cuenta Max Bill, la que está en la segunda fila y segunda columna. Aunque está también es simétrica a uno de los patrones de las de la clasificación de Max Bill, el patrón X.

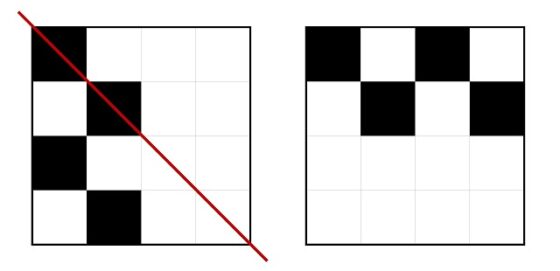
En consecuencia, Max Bill realizó una clasificación completa de todas las estructuras básicas posibles para su serie de obras 11 x 4 : 4, sin dejarse ninguna fuera, como hemos comprobado mediante esta pequeña reflexión matemática sobre su proceso creativo. Dicho de otra forma, el proceso creativo de Max Bill utiliza elementos de la geometría, el álgebra y la combinatoria.

Bibliografía

1.- R. Ibáñez, Las matemáticas como herramienta de creación artística, Libros de la Catarata – FESPM, 2023.

2.- Max Bill, El pensamiento matemático del arte de nuestro tiempo, 1949.

3.- Valentina Anker, Max Bill ou la recherche d´un art logique, Editions l´Age d´Homme, 1979

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica