“… ninguna rama de la actividad intelectual es más adecuada para el debate que los juegos de ingenio y las paradojas.

…los juegos de ingenio, en cierto sentido, reflejan mejor que cualquier otra rama de las matemáticas, su espíritu siempre joven, puro y curioso. Cuando alguien deja de preguntarse y jugar, está acabado. Los juegos de ingenio están hechos de la materia con la que, al igual que los niños, juegan, sueñan y sobre la que se cuestionan, los matemáticos, pues están hechos de las cosas y circunstancias del mundo en el que viven.”

(Matemáticas e imaginación, E. Kasner, J. Newman)

Los juegos son, y han sido desde la antigüedad, una parte importante de nuestra cultura, de nuestra sociedad. Todas las personas, desde las más jóvenes a las más mayores, disfrutan jugando. Por este motivo, en la categoría Matemoción del Cuaderno de Cultura Científica nos gusta incluir de vez en cuando alguna entrada sobre juegos relacionados de alguna manera con las matemáticas, en particular, juegos de ingenio. Entradas dedicadas a estos juegos han sido…

Mujeres jugando (el juego del molino)

Tangram

Tchuka Ruma, el mancala solitario

El juego coreano Kono

El salto de la rana, y familia

Os recomiendo que las visitéis. Encontraréis juegos que os permitirán pasar agradables momentos, solos o en compañía, así como comentarios interesantes sobre los mismos, su historia y matemáticas.

Hoy vamos a dedicar esta entrada del Cuaderno de Cultura Científica a un juego muy antiguo y extendido por todo el mundo, el mancala.

Mancala es el nombre genérico que se utiliza para nombrar a toda una familia de juegos, que se suelen jugar entre dos personas, cuyo tablero consiste en varias filas (dos, tres o cuatro) de agujeros, en el suelo o en un bloque de madera, sobre los que se depositan fichas, o “se siembran semillas”, y cuyo objetivo es la captura, o “recolección”, de estas. Son juegos relacionados con la actividad agrícola. El número de agujeros por fila puede variar mucho de unas zonas a otras, desde 3 o 4 hasta 36 o más aún, siendo en este último caso difícil de jugar únicamente por dos personas, por lo que es habitual que se hagan equipos.

Awari, ayo, ba-awa, congklak, dakon, endodoi, kalah –juego moderno inventado en EEUU en 1940-, kale, leab el-akil, mankal’ah l’ib al-ghashim, mbau, pallanguzhi, sungka, toguz khorgol, wa-we (de dos filas), gabata, selus (de tres filas, que son menos habituales que los otros) o bao, chuba, kiarabu, moruba, omweso, owela (de cuatro filas), son algunos de los juegos de esta familia. La palabra “mancala”, que es el nombre del juego de esta familia que se practica en Siria y Egipto, es una palabra árabe que significa “mover o trasladar”.

Los juegos de tipo mancala están muy extendidos por todo el mundo. A lo largo de toda África, Oriente Medio, sur y centro de Asia, Caribe y las Guayanas, y más recientemente, otras partes de América y Europa. Es bastante probable que su origen esté en algún lugar de África (quien sabe si Egipto o Etiopía, aunque se desconoce realmente), y que fuesen los comerciantes árabes quienes los llevaron a Oriente Medio, y de ahí penetrase en Asia. Mientras que los esclavos de origen africano fueron quienes lo llevaron a América. El mancala estuvo presente en diferentes lugares de Europa y en diferentes épocas, a través de sus relaciones con pueblos que jugaban al mismo, pero poco a poco iría desapareciendo.

Se desconoce la edad y el origen de estos juegos. Por una parte, la tradición oral de los pueblos africanos en los que se pudo originar y jugar durante siglos, así como lo efímero de los tableros en los que se jugaba (generalmente, filas de agujeros excavados en la tierra o arena, y tableros de madera) dificulta la investigación sobre la edad de estos juegos (que podrían tener más de 3.500 años), así como el lugar donde se originaron.

Se suele considerar que los tableros de mancala más antiguos descubiertos son una serie de grupos de agujeros tallados en piedra en los templos de Kurna y Karnak (Egipto) y descritos por Henry Parker en 1909. Estos templos fueron fechados hacia el 1.400 a.c. Así mismo, Parker también escribe que encontró similares agujeros en la pirámide de Menkaura (hacia el 2.500 a.c). Sin embargo, los arqueólogos modernos y expertos en juegos de tablero que han intentado encontrarlos no lo han conseguido, y los únicos agujeros de este tipo que han sido hallados no parecen ser, según los expertos (como por ejemplo, el arqueólogo Ulrich Schadler, director del Museo Suizo del Juego y profesor de la Universidad de Freiburg, o el experto en historia de juegos de tablero, Thierre Depaulis), tableros de algún juego de la familia mancala. De hecho, podrían ser tableros de otro tipo de juegos o agujeros destinados a la contabilidad, pero incluso tampoco está claro que esos agujeros fueran realizados en la época de construcción del templo, y podrían ser muy posteriores.

Algo similar ocurre con algunas series de agujeros encontradas en yacimientos neolíticos, como Beidha (Jordania), hacia el 7.000 a.c., o ‘Ain Ghazal, anterior al 5.000 a.c, que no parecen tableros de mancala. O con otras familias de agujeros descubiertas por la paleoantropóloga Mary Leakey en el asentamiento prehistórico de Hyrax Hill (Kenia), fechado sobre el 1.500 a.c. También se han encontrado marcas que sugieren la posibilidad de un tablero de mancala en asentamientos romanos, de los primeros siglos de nuestra era, como por ejemplo una fortaleza romana en Abu Sha’ar, en la costa del mar rojo en Egipto.

El primer tablero sobre el que los expertos están de acuerdo en asegurar que es un mancala es un tablero de cerámica que se encontró en Aksumite, Etiopia (así mismo, también hay varias series de filas de agujeros sobre piedra que podrían ser tableros de mancala), que está datado entre los siglos VI y VII d.c.

Los dos primeros textos conocidos en los que se hace mención al mancala son de finales del primer milenio y de la zona de Oriente Medio. El primero es un libro persa, escrito por Abu abd-Allah Muhammad el-Gahshigar en el siglo IX, y que es el núcleo central de la célebre recopilación medieval de cuentos árabes “Las mil y una noches” (Hazār-o yak shab). Mientras que el segundo es la recopilación persa de canciones y poemas “El libro de las canciones” (Kitab al-aghani), de Abu al-Faraj al-Isfahani.

Del siglo X es un tablero de un juego de la familia mancala encontrado en el Monasterio de Santo Domingo de Silos, que pertenecía a una de las hijas de Abd-al-Rahman III (891-961), emir y primer califa de Córdoba, y que se exhibe en el Museo de Burgos. La pieza es un estuche de marfil con forma cilíndrica, en cuyo interior, al abrir el estuche por la mitad, se tienen dos filas de cinco huecos semiesféricos cada una, realizada en talleres cordobeses de Medina Azahara. Consta de una inscripción que dice «Esto fue hecho para la señora hija de Abd-al-Rahman principe de los creyentes». Según parece fue entregado al Monasterio de Santo Domingo de Silos por el Conde Fernán González, como parte de una ofrenda del botín conseguido en la batalla de Osma.

Esta pieza recuerda a los tableros del awalé (aunque con 5 agujeros en cada fila, en lugar de los 6 del awalé), como el que aparece en la siguiente imagen. Aunque existen juegos de la familia del mancala que tienen 5 agujeros en cada una de las dos filas, como algunas versiones de los juegos dakon, congklak o sungka.

Así mismo, en la ciudad musulmana Ciudad de Vascos (en Navalmoralejo, Toledo), construida en el siglo X y abandonada en el XI, los arqueólogos Yolanda Cosín Corral y Constantino García Aparicio según han publicado en la Revista de Arqueología, podrían haber encontrado 12 tableros de mancala, y también tableros de otros juegos, como el Alquerque.

Pero lo más interesante de un juego es… jugar. Por lo tanto, vayamos con las reglas de uno de los juegos más extendido de tipo Mancala, el awari (también conocido con los nombres awalé, oware o wari). Es un juego para dos jugadores. El tablero del awari consiste en dos filas de 6 hoyos, con 4 semillas en cada uno de ellos, y opcionalmente, dos hoyos en los laterales para colocar las semillas que recolecta cada uno de los jugadores.

Los dos jugadores irán moviendo por turnos. Cada movimiento se divide en dos partes, la siembra y la recolección. Cada jugador mueve semillas de “su” fila (la más cercana) y recolectará de la fila de su oponente.

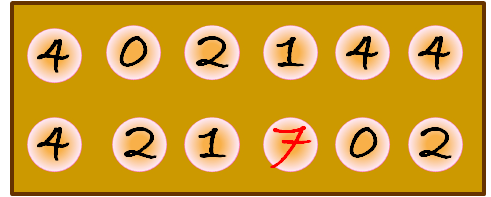
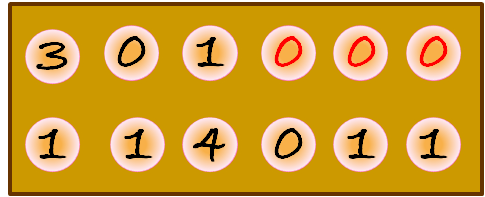
Siembra: cada jugador (por turnos) elegirá uno de “sus” hoyos y distribuirá las semillas que contiene, una a una, en los siguientes hoyos, en el sentido contrario a las agujas del reloj (pudiendo darse la vuelta completa, sin sembrar en el hoyo inicial).

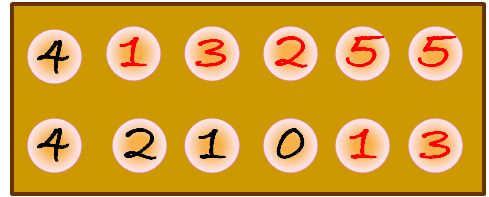
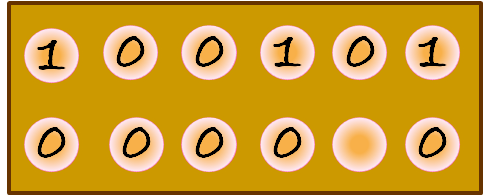
Si el jugador cuya fila es la de abajo siembra las 7 semillas del agujero que se marca en rojo en la primera imagen, las semillas quedan repartidas en los siguientes agujeros, siguiendo el sentido contrario a las agujas del reloj, como se muestra en la segunda imagen

Si un jugador no puede sembrar en su turno, porque no hay semillas en sus agujeros, el otro deberá realizar una siembra que le proporcione semillas.

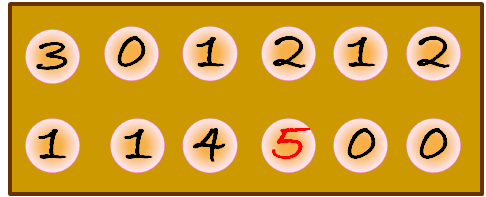
Recolección: si la última semilla sembrada cae en un hoyo rival que contenga 2 o 3 semillas (tras la siembra), estas son capturadas por el jugador.Una vez realizada la captura, si el hoyo anterior también contiene 2 o 3 semillas, se capturan, y así hasta que se llegue a un hoyo en el que no sea posible la recolección o al extremo de los huecos del jugador contrario.

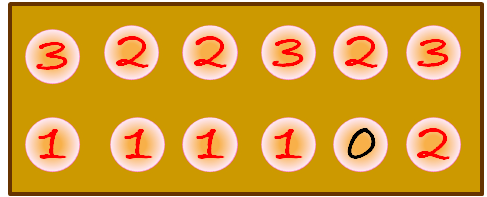
Jugada de siembra y recolección

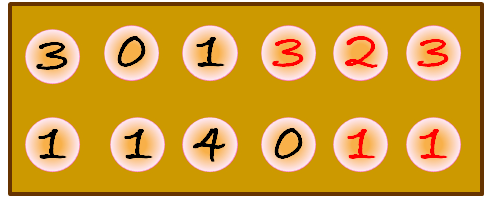
Un jugador no puede realizar una siembra que deje al adversario sin semillas (si es la única jugada posible o ya se ha realizado, se realiza la siembra, pero sin recolección).

En esta jugada del jugador de la fila de abajo, al realizar la correspondiente recolección dejaría sin semillas al jugador de la fila de arriba, por lo cual no se puede realizar esa siembra y en caso de haberse realizado, entonces no se podrán recolectar las semillas

El final de la partida se producirá en alguno de los siguientes casos:

i) un jugador no tiene semillas en su lado y el otro jugador no puede suministrárselas en una sola jugada, en este caso este último jugador se queda con las semillas del tablero y gana el que tenga más semillas;

ii) hay pocas semillas y se entra en bucle, entonces cada jugador se queda con las de su fila y gana el que más fichas tenga;

iii) un jugador ha conseguido capturar más de 24 semillas, y gana la partida.

Imagen 12 (Pie de imagen: tablero para jugar al bao o al kiarabu)

Las reglas de otros juegos de la familia mancala, como por ejemplo el congklak, el kalah, el sungka, el ayo o el kiarabu, pueden encontrase en la literatura que se recomienda en la bibliografía de esta entrada. Así mismo, existen algunos juegos de la familia mancala pensados para un solo jugador. Uno es el tchuka ruma, del que ya hablamos en el Cuaderno de Cultura Científica.

Para finalizar, el awari, como muchos otros juegos, en especial los que podríamos llamar “matemáticos”, son de gran interés en el campo de la inteligencia artificial, donde se desarrollan algoritmos para resolverlos.

En 2002, John W. Romein y Henri E. Bal (Universidad Libre de Amsterdam) demostraron que si los dos jugadores “jugaban a la perfección” al awari, quedarían en tablas, como ocurre en el conocido juego del tres en raya, aunque en este último juego es mucho más sencillo de probar. Para demostrar que el juego acaba forzosamente en tablas si lo jugasen jugadores “perfectos”, los informáticos Romein y Bal elaboraron un programa informático que analizó los resultados de las 889.063.398.406 posiciones posibles del juego, para lo cual se necesitaron 51 horas de cálculos realizados por un grupo de ordenadores en paralelo con 144 procesadores.

Tableros de mancala (de izquierda a derecha y de arriba a abajo) de Guinea-Biassau, Sierra Leona, Uganda y de la cultura Tuareg, pertenecientes al Museo de Brooklyn

Bibliografía

1.- Juan Diego Sánchez Torres, Juegos de tablero, para el aula y otros lugares, Ed. CCS, 2008.

2.- Claudia Zaslaski, Math games and activities around the world, Chicago Review Press, 2003

3.- Robbie Bell, Michael Cornelius, Juegos com tablero y fichas, Estímulos a La investigación matemática, Labor, 1990.

4.-Awalé, www.awale.info

5.- Stewart Culin, Mancala, the national game of Africa, Smithsonian Institution, United States National Museum, 1896.

6.- Alex de Voogt, Mancala, Games that Count, Expedition 43, n.1, 2001, p. 38-46.

7.- Philip Townshend, African Mankala in Antropological Perspective, Current Anthropology 20, n. 4, 1979, p. 794-796.

8.- Ralf, Gering, Mancala timeline

9.- Museo de Burgos

10.- Revista Mon Aualé. Revista divulgativa de los juegos mancala (en catalán)

11.- Y. Cosín Corral, C. García Aparicio, Alquerque, mancala y dados: juegos musulmanes en la ciudad de vascos, Revista de Arqueología 19, n. 201, p. 38-47.

12.- Tableros de mancala de Al-Andalus

13.- Clifford A. Pickover, El libro de las matemáticas, Librero, 2009.

14.- John W. Romein y Henri E. Bal,Solving the Game of Awari using Parallel Retrograde Analysis, IEEE Computer 36, n. 10, 2003, p. 26-33.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica