En la primera entrada de esta mini-serie de la sección Matemoción del Cuaderno de Cultura Científica, El puzle Stomachion y el palimpsesto de Arquímedes (1), habíamos descrito el rompecabezas conocido como Stomachion, o caja de Arquímedes, e incluso analizado las áreas de las piezas que lo componen, pero, sobre todo, habíamos contado la sorprendente historia del palimpsesto de Arquímedes, que incluye la copia más extensa de la obra Stomachion del gran matemático griego Arquímedes de Siracusa (aprox. 287 – 212 a.n.e.). Por otra parte, en la presente entrada vamos a centrarnos en algunos aspectos matemáticos del Stomachion.

Empecemos recordando que el Stomachion es un rompecabezas de tipo Tangram formado por 14 piezas, en concreto, 11 triángulos, 2 cuadriláteros y 1 pentágono, que podemos ver en la imagen anterior.
Si consideramos que el cuadrado generador tiene unas dimensiones de 12 unidades de longitud (por ejemplo, centímetros) de lado y trazamos la cuadrícula 12 x 12 sobre el mismo, como hicimos en la entrada anterior, se puede observar que todos los vértices de las piezas descansan sobre los puntos de intersección de la cuadrícula. Notemos además que, en la cuadrícula, la distancia entre un punto de la misma y el siguiente, en horizontal o vertical, es una unidad de longitud. Esto, además de dejar claro que esta descomposición del cuadrado no es caprichosa, nos permite calcular fácilmente las áreas de las 14 piezas del rompecabezas, todas con valores enteros (desde arriba a la izquierda, siguiendo el orden de las agujas del reloj, más o menos): 12, 6, 12, 24, 3, 9, 6, 12, 6, 21, 3, 6, 12 y 12.
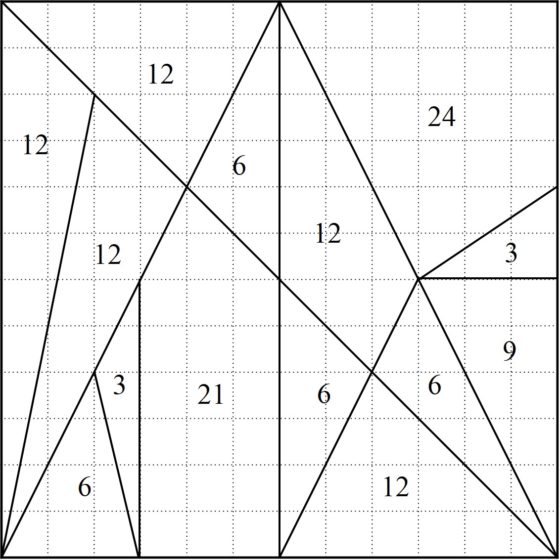
El cálculo de las áreas es sencillo y puede ser un interesante problema para el aula de matemáticas, pero aún le podemos sacar un poco más de partido al tema de las superficies, comprobando que los anteriores resultados son correctos mediante el teorema de Pick, como nos sugiere el grupo Alquerque de Sevilla en su artículo sobre el Stomachion en la revista Suma.
Teorema de Pick (1899): si un polinomio P tiene sus vértices sobre una cuadrícula, entonces su área es igual a
donde B es un número de puntos de la cuadrícula que están en el borde del polígono e I los que están en el interior del mismo.
En la siguiente imagen podemos ver la comprobación del teorema de Pick para las piezas verde y azul. Hemos pintado los puntos del borde de los polígonos (cuyo número es B) de amarillo y los del interior de verde (cuyo número es I).
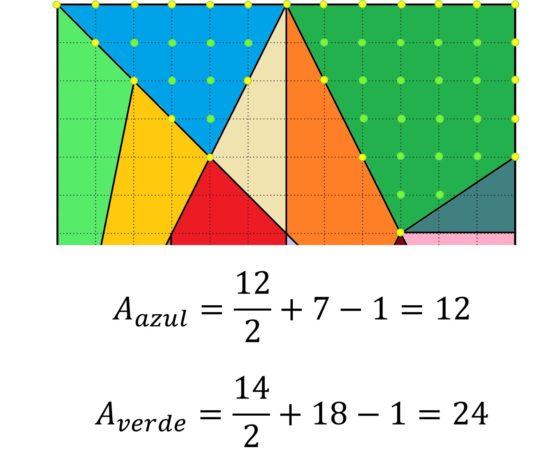
A continuación, vamos a analizar los ángulos de las piezas de la caja de Arquímedes. Esta es una cuestión importante también, puesto que cuando se trabaja la resolución de puzzles geométricos como el Tangram, los rompecabezas de letras, como T y M, u otros similares, el razonamiento sobre los ángulos es fundamental para la resolución de los mismos. Por ejemplo, en estos puzzles cuadrados, en las esquinas debe ir una pieza rectangular o la suma de los ángulos de las piezas que tocan la esquina debe ser 90º, los ángulos en los vértices que están en los lados del cuadrado deben sumar 180º, mientras que en los vértices interiores deben sumar 360º (véase en la imagen algunos ejemplos).
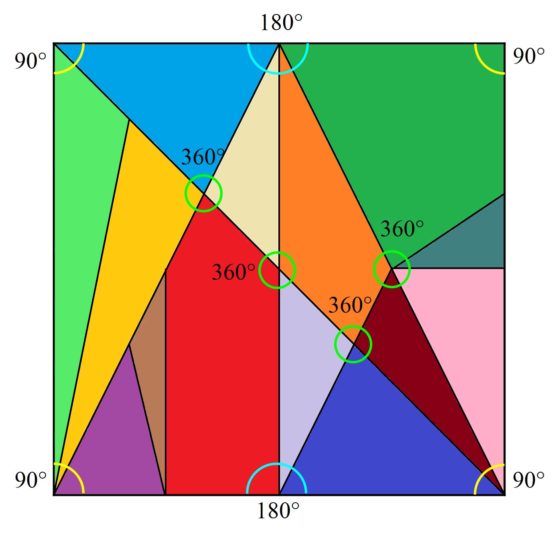
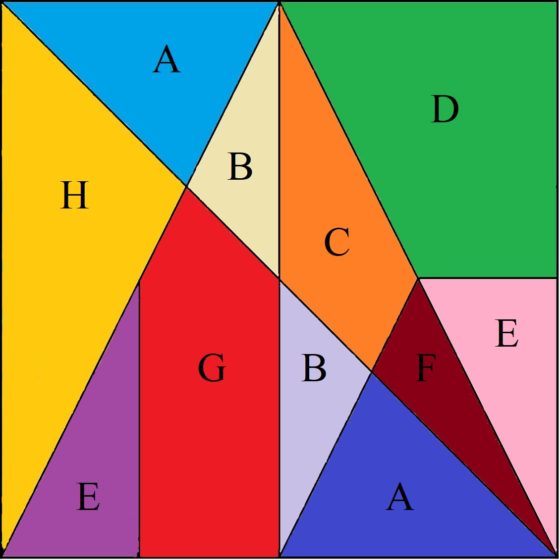
Para empezar, fijémonos en la pieza que es un triángulo rectángulo, de área 3 en la cuadrícula 12 x 12, que está en la parte derecha de la imagen anterior del puzzle (de color azul grisáceo en la imagen coloreada). Si estudiamos los ángulos de esta figura, uno es 90º (ángulo recto), pero los otros son alpha = arctan (2/3) = 33,69º (aprox.) y beta = 90º – alpha = 90º – 33,69º = 56,31º (aprox.). Como veremos más adelante, la mayoría de los ángulos de las piezas del Stomachion están relacionados con el ángulo delta = arctan (1/2) = 26,57º (aprox.) y los ángulos alpha y beta de este pequeño triángulo rectángulo solo encajan con los ángulos alpha’ y beta’ de la pieza que es un cuadrilátero con un ángulo recto (la pieza verde oscuro en la imagen coloreada). Como consecuencia de esto las dos piezas anteriores, el cuadrilátero con un ángulo recto y el pequeño triángulo rectángulo, siempre irán juntas en cualquier solución del juego original, es decir, colocar las piezas del rompecabezas para montar un cuadrado.
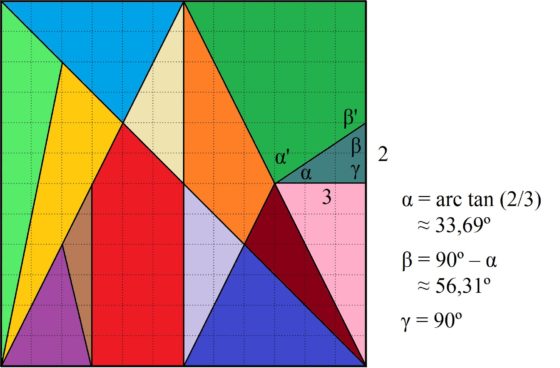
Un análisis similar puede realizarse con las piezas verde claro y naranja, que irán juntas en cualquier solución de la caja de Arquímedes. Y lo mismo las piezas morada y marrón. Por este motivo, en los análisis matemáticos de este juego geométrico se suele juntar cada una de estas parejas de piezas para formar una pieza común. De hecho, la matemática estadounidense nacida en Taiwán Fan Chung y el matemático estadounidense Ron Graham llaman a este nuevo puzzle el Stomach (le han quitado tres letras al nombre, al igual que el nuevo rompecabezas ahora tiene tres piezas menos), y veremos más adelante el análisis que hacen del mismo.
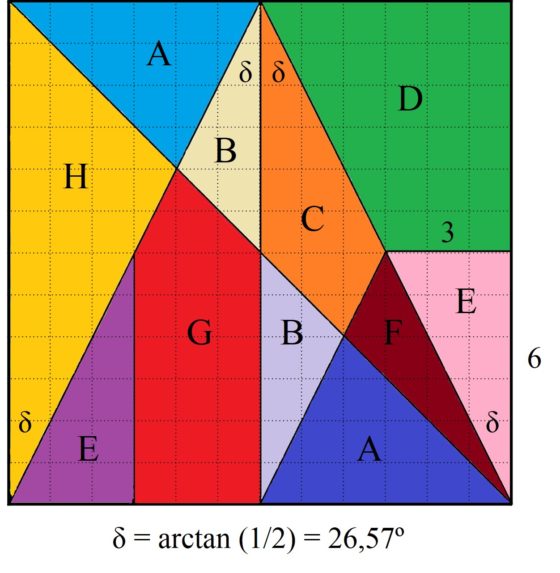
Ahora, de nuevo con un poco de trigonometría básica (de hecho, basta la definición geométrica de la tangente de un ángulo y que la suma de los ángulos de un triángulo es 180º) se pueden calcular los ángulos de las piezas del Stomach (en general, del Stomachion), que como hemos comentado están la mayoría expresados en función del ángulo delta = arctan (1/2) = 26,57º (en la imagen siguiente puede verse, por ejemplo, en el triángulo rosa que el ángulo delta es aquel cuya tangente vale 3/6 = 1/2).
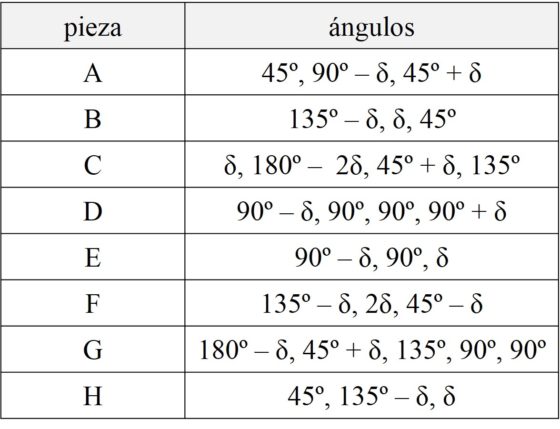
A continuación, mostramos en una tabla los valores de los ángulos de las piezas del Stomach (que son las del Stomachion, con la salvedad de las tres uniones que hemos realizado). Empezamos por las piezas de arriba a la derecha, desde la pieza A, y enumeramos los ángulos desde la derecha y en el sentido de las agujas del reloj.
Pero volvamos a la obra Stomachion de Arquímedes, dedicada al rompecabezas homónimo. Como comentamos en la anterior entrada El puzzle Stomachion y el palimpsesto de Arquímedes (1), el mayor fragmento conservado de esta obra, aunque es solamente una página y además la parte introductoria de la misma, apareció en el palimpsesto de Arquímedes. Esta obra despistó completamente a los expertos, ya que aparentemente trataba sobre un juego infantil sin ningún interés científico, lo cual no se correspondía con la profundidad científica de sus demás obras.
El historiador de las matemáticas israelí Reviel Netz, profesor de la Universidad de Stanford en California, después de investigar el Stomachion concluyó que, en su opinión, no era simplemente una sencilla obra sobre un juego infantil, sino que se trataba realmente de un tratado de combinatoria.
La combinatoria es una rama de las matemáticas, que entre otras cuestiones incluye el estudio de métodos para contar las estructuras o configuraciones de un conjunto de un determinado tipo o tamaño. Por ejemplo, son problemas de la combinatoria el contar cuántos cuadrados latinos existen de un orden dado (véase la entrada Cuadrados latinos, arte y matemáticas), cuántas soluciones tiene una ecuación lineal (véase Aprendiendo técnicas de contar: lotería primitiva y bombones), cómo se pueden distribuir una serie de elementos con unas ciertas condiciones (véase El problema matemático de las cartas extraviadas o El problema de las estudiantes de Kirkman), o cuántas soluciones tiene un juego o puzzle (véase Cubo soma: diseño, arte y matemáticas o el libro Del ajedrez a los grafos).
En opinión de Reviel Netz la cuestión que le interesaba a Arquímedes en relación al rompecabezas era cuántas soluciones existen del mismo, es decir, de cuántas formas distintas se pueden colocar las 14 piezas para formar un cuadrado. Mientras que para el Tangram solo hay una manera de construir el cuadrado, es decir, solo existe una solución, más allá de rotaciones (girar el cuadrado), reflexiones (darle la vuelta) o cambiar las piezas de igual forma entre sí, las piezas geométricas del Stomachion se pueden combinar de diferentes formas para dar lugar al cuadrado, esto es, tiene muchas soluciones. Este era el problema combinatorio del tratado de Arquímedes, por lo tanto, de una profundidad mayor de la que aparentaba.
Por lo tanto, el problema combinatorio quedaba abierto, ¿de cuántas formas distintas se puede resolver la caja de Arquímedes? El profesor Netz no sabía cómo de difícil podía ser este problema y si Arquímedes pudo resolverlo en su tratado, por lo que se lo planteó a algunos colegas de su universidad, la profesora de estadística Susan Holmes y el matemático Persi Diaconis, conocido por su trabajo en magia y matemáticas. Como explica la propia Susan Holmes: “al principio pensamos que podíamos sentarnos y resolver en un día cuántas soluciones tenía. Entonces nos dimos cuenta de que eran muchas más de las que podíamos haber imaginado”. Entonces, junto con la pareja de profesores de la Universidad de California, Ron Howard y Fan Chung, dedicaron varios meses a resolver esta cuestión combinatoria. Finalmente, obtuvieron la respuesta buscada, hay 17.152 configuraciones distintas de todas las piezas del Stomachion que forman un cuadrado, que se reducen a 536, si no tenemos en cuenta rotaciones, reflexiones o el intercambio de las piezas que son iguales (las piezas A y B en la imagen del Stomach), 536 x 32 = 17.152.

Aunque un poco antes, en noviembre de 2003, el informático Guillermo H. Cutler, que había diseñado un programa informático para resolver el problema, encontró las 536 formas distintas de combinar las 14 piezas del rompecabezas para formar el cuadrado.

Por otra parte, la profesora Chung y el profesor Graham visualizaron las soluciones de la caja de Arquímenes, y las relaciones entre las mismas, a través de un grafo, que vamos a explicar brevemente en lo que queda de entrada. La construcción es delicada, pero de una gran profundidad y belleza.
Para empezar, Fan Chung y Ron Howard no estudiaron directamente las soluciones del Stomachion, sino de un nuevo rompecabezas que llamaron Stomach y que hemos mostrado más arriba. Las soluciones son prácticamente las mismas. De hecho, cada solución del Stomach da lugar a dos soluciones del Stomachion ya que la pieza E rosa, se puede intercambiar con la pieza E morada, la cual está formada por dos piezas del Stomachion original. De hecho, el Stomach tiene 268 configuraciones básicas, que dan lugar a las 268 x 2 = 536 configuraciones básicas del Stomachion.
Para visualizar las soluciones del Stomach, Chung y Howard construyeron un grafo. Recordemos que un grafo está formado simplemente por puntos –llamados vértices del grafo- y líneas que unen algunos de esos puntos –llamadas aristas del grafo- (véase, por ejemplo, El problema de los tres caballeros y los tres criados [https://culturacientifica.com/2016/05/04/problema-los-tres-caballeros-los-tres-criados/], El grafo de Marion (gray) [https://culturacientifica.com/2019/07/31/el-grafo-de-marion-gray/] o El juego de Sim [https://culturacientifica.com/2017/04/19/juego-del-sim/], entre otros), y que es una estructura matemática muy sencilla, pero a la vez muy versátil.
En el grafo introducido por Chung y Howard, asociado al rompecabezas geométrico, cada vértice es una de las configuraciones de las piezas formando el cuadrado, es decir, una de las 268 soluciones del rompecabezas, mientras que dos vértices están unidos por una arista si existe un movimiento, local o global (cuyo significado explicaremos un poco más adelante), que transforma una configuración en otra.
Para empezar, describamos lo que esta pareja de matemáticos denomina “núcleo” del grafo, que está formado por 24 configuraciones particulares y los movimientos entre ellas.
Si se consideran las 11 piezas del Stomach, solo existe una forma de dividirlas en cuatro grupos para formar cuatro triángulos rectángulos básicos, que juntos dan lugar al cuadrado del rompecabezas, que llamaremos triángulos básicos 1, 2, 3, 4, siguiendo la notación de Chung y Howard. Estos triángulos son:
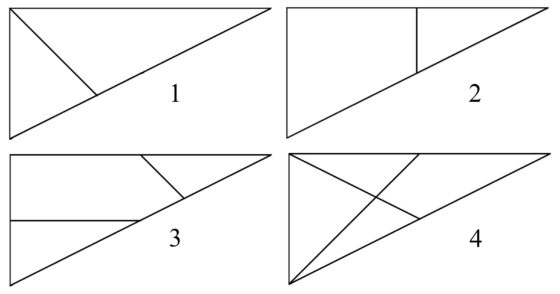
El núcleo del grafo está formado por las 24 soluciones básicas que se obtienen juntando estos cuatro triángulos, tomados tal cual están, salvo que los rotemos, o volteados. La notación que vamos a utilizar es la siguiente. Cada configuración básica estará nombrada por los cuatro números de los cuatro triángulos básicos en el orden que están colocados desde la izquierda a la derecha, y si un triángulo está volteado utilizamos un signo prima para marcarlo. Por ejemplo, la solución inicial del Stomach que está más arriba, coloreada, sería 1’ 2’ 3 4, ya que la pieza 1 está a la izquierda, pero volteada, lo mismo que la siguiente, que es la 2, mientras que luego van, sin voltear, las piezas 3 y 4.
A continuación, mostramos la imagen con las 24 configuraciones del núcleo, con la correspondiente notación.
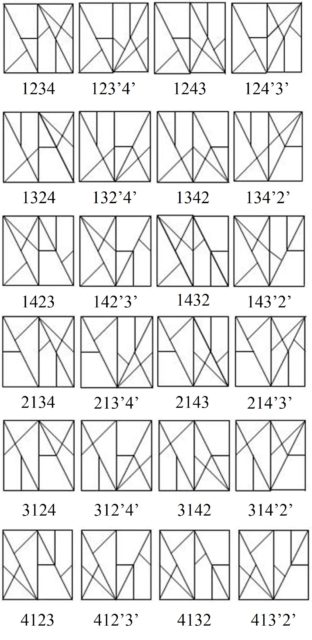
Además, estas configuraciones del núcleo están conectadas por movimientos globales (que van a ser las aristas del grafo) que consisten en intercambiar dos de los cuatro triángulos básicos (la pieza 1 la podemos mantener sin dar la vuelta y siempre en la parte de la izquierda, respecto al centro).
Por ejemplo, la configuración 1234 está conectada, con una arista, a las configuraciones 1324, 1243, 124’3’, 123’4’ y 2134, puesto que se puede llegar a ellas intercambiando dos de los triángulos básicos de 1234, como se ve fácilmente. En teoría de grafos se dice que el vértice 1234 tiene grado 5, ya que hay 5 aristas conectadas con el mismo (por ahora).
Podemos formar ahora la parte de este grafo que es el núcleo, cuyos vértices son las 24 configuraciones anteriores y las aristas están dadas por los movimientos globales que acabamos de describir. El resultado sería el siguiente.
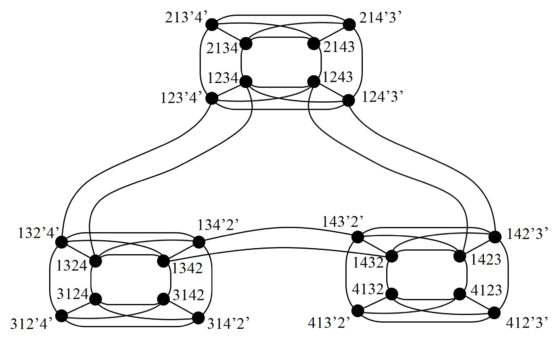
Por otro lado, cada una de esas 24 configuraciones básicas está conectada, mediante aristas que vienen de movimientos locales, con otras configuraciones del cuadrado. Un movimiento local de una configuración consiste en rotar o voltear una subregión simétrica del cuadrado formada por un grupo de piezas contiguas. Por ejemplo, en la imagen de abajo el grupo de piezas formado por los dos triángulos azules, que es un triángulo isósceles, ha sido volteado para dar lugar a otra solución distinta del rompecabezas, otra configuración.
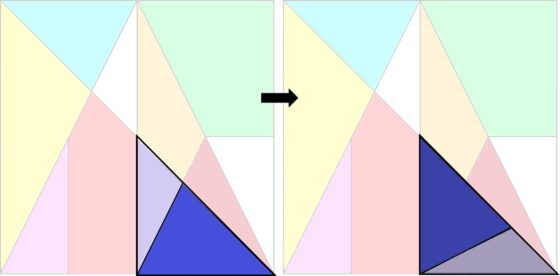
Dada una de las 24 configuraciones básicas, llamémosle B, la estructura de las configuraciones que se pueden alcanzar a partir de ella, mediante movimientos locales, es denominada por Chung y Howard el “cluster” de B. En la siguiente imagen vemos el cluster de la configuración básica 1234, con el grafo asociado al mismo, que es un grafo con 7 vértices/representaciones (podéis descubrir en la imagen el movimiento local que se produce entre una configuración y otra conectada). Notemos que se han coloreado los vértices en función de la distancia a la configuración básica del núcleo (cada arista recorrida aumenta una unidad la distancia), en este ejemplo, la distancia a 1234.
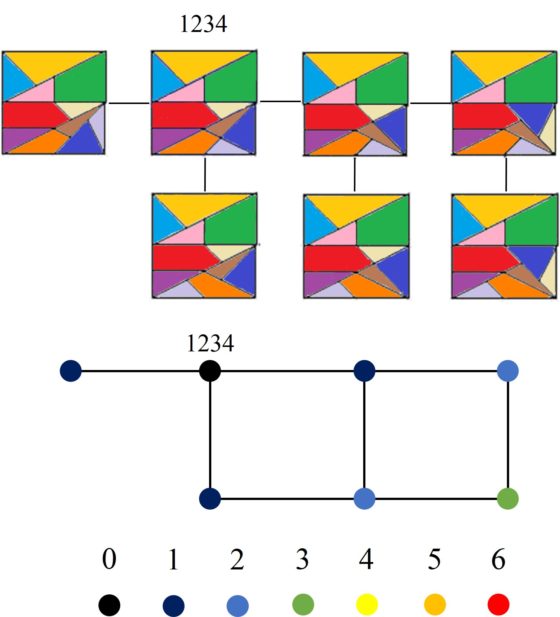
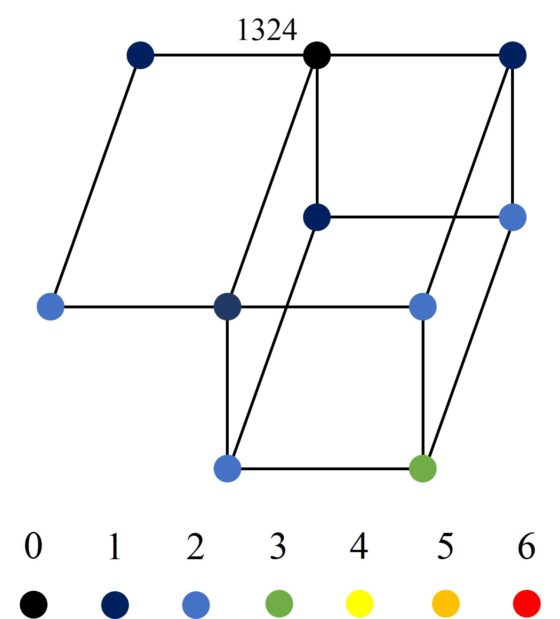
Los clusters de las configuraciones básicas no son siempre iguales. Por ejemplo, el cluster de la configuración 1324 tiene diez vértices, como vemos en la siguiente imagen.
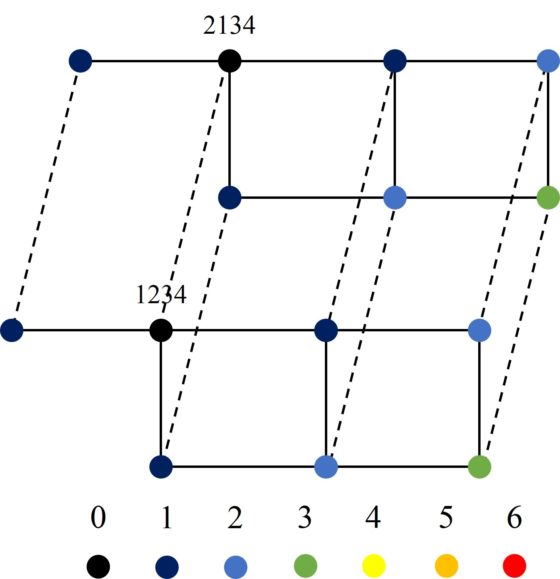
Además, la arista entre dos vértices del núcleo, es decir, entre dos configuraciones básicas, se extiende a aristas entre los vértices de sus clusters. Si los clusters tienen la misma estructura, como los de los vértices 1234 y 2134, las aristas se extienden de forma paralela, como se ve en la siguiente imagen.
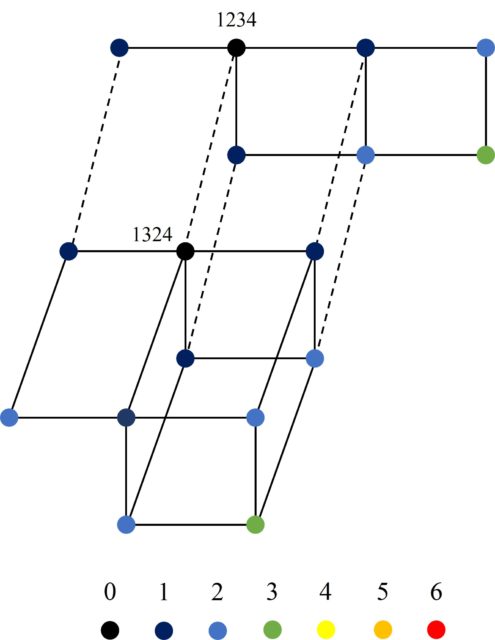
Mientras que, si los clusters tienen distintas estructuras, entonces las aristas que unen vértices de los dos clusters son más particulares, como entre los vértices 1234 y 1324.
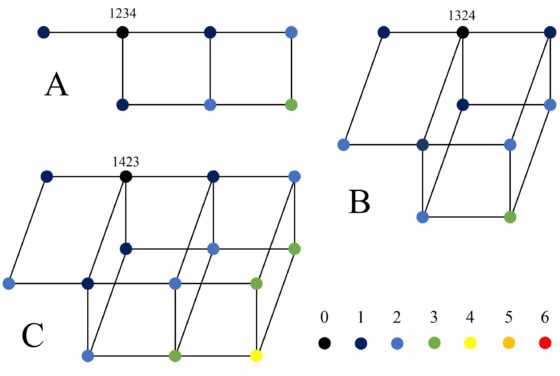
Existen seis estructuras diferentes de clusters, aunque la mayoría de las configuraciones básicas están relacionadas con tres de ellos. La estructura del cluster de las ocho configuraciones básicas que están en la parte superior de la imagen del grafo del núcleo (1234, 1243, 2143, 2134, 213’4’, 123’4’, 124’3’, 214’3’) es la misma. La llamaremos “estructura de cluster A” y tiene 7 vértices. También comparten estructura de cluster seis de las ocho configuraciones básicas que están en la parte izquierda de la imagen del grafo del núcleo (1324, 3124, 3142, 132’4’, 312’4’, 314’2’). La llamaremos “estructura de cluster B” y tiene 10 vértices. Y la otra estructura de cluster repetida, que llamaremos “estructura de cluster C”, tiene 14 vértices y es compartida por 7 de las ocho configuraciones básicas que están en la parte derecha de la imagen del grafo del núcleo (1423, 4123, 4132, 143’2’, 142’3’, 412’3’, 413’2’). Estas tres estructuras de clusters son las que aparecen en la siguiente imagen.
Mientras que hay tres configuraciones básicas, cada una de las cuales tiene su propia estructura particular de cluster. La configuración 1432 tiene la siguiente estructura de cluster, que llamaremos D, con 18 vértices.
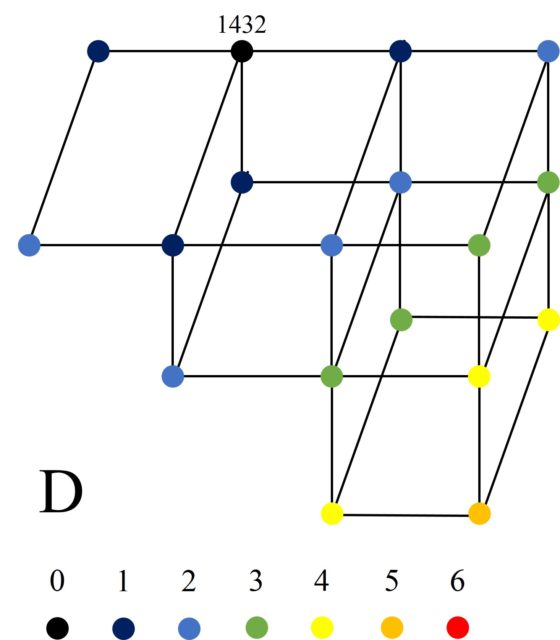
La configuración 1342 tiene la estructura de cluster que llamaremos E, con 16 vértices.
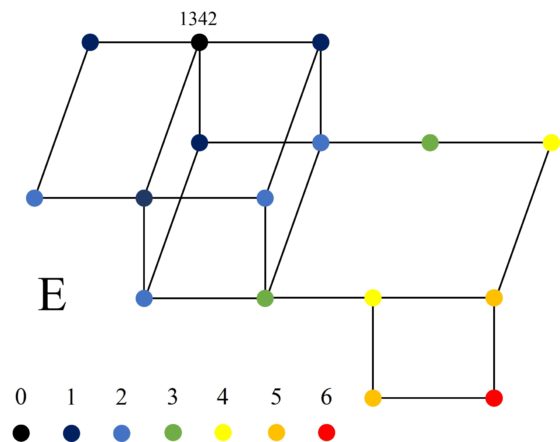
Y la configuración 134’2’ tiene la estructura de cluster más raras de todas, también con 18 vértices, que llamaremos F.
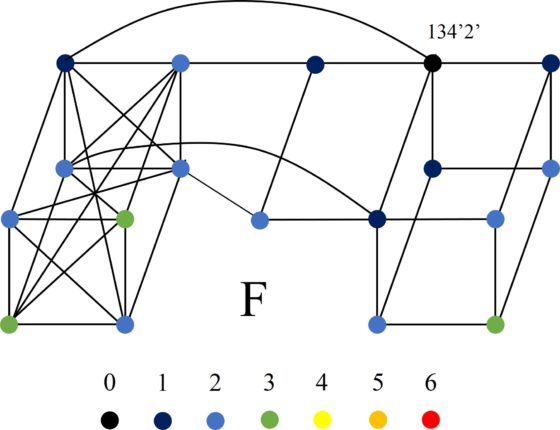
En resumen, el grafo gigante que hemos generado con soluciones/configuraciones del Stomach posee 266 vértices (que recordemos que son las soluciones del rompecabezas geométrico) y 936 aristas (que recordemos que están generadas a partir de movimientos locales y globales sobre las soluciones del Stomach). Pero resulta que hemos generado un grafo (conexo, es decir, no hay grupos de vértices desconectados, mediante las aristas, del resto) con 266 vértices, pero recordemos que el número de soluciones básicas del Stomach son 268. ¿Qué ocurre con las otras dos soluciones/configuraciones del puzzle? Resulta que esas dos configuraciones, están conectadas entre ellas mediante un movimiento local, es decir, son dos vértices con una arista entre ellas, pero están desconectadas del resto de soluciones del rompecabezas. Estas configuraciones son las que aparecen en la imagen siguiente.
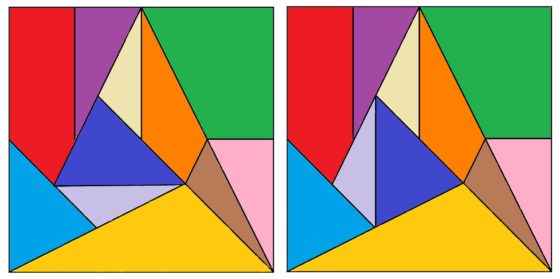
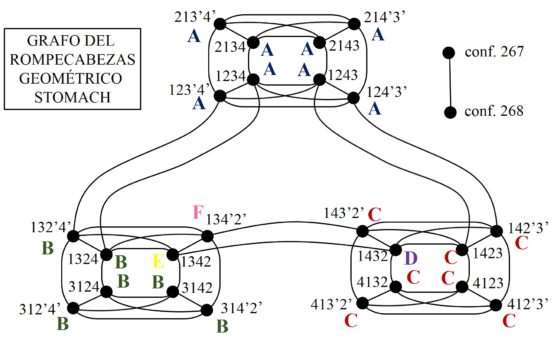
En la siguiente imagen, para comprender un poco mejor la estructura de este enorme grafo asociado con el puzzle geométrico Stomach, hemos vuelto a dibujar el núcleo, indicando en cada configuración básica cual es la estructura de cluster que se agrega a la misma, así como las dos configuraciones aisladas, que no están en el núcleo o conectadas con el mismo, que hemos denominado “configuración 267” y “configuración 268”.
Todos los detalles de esta construcción, incluidas las aristas entre clusters de diferente estructura que no hemos incluido aquí, pueden encontrarse en la página A tour of Archimedes’ Stomachion, de la matemática Fan Chung y el matemático Ron Graham. Además, se incluyen interesantes propiedades matemáticas del grafo, como las dos con las que concluimos esta entrada.
Si consideramos la componente más grande del grafo del Stomach, con 266 vértices y 936 aristas, esta tiene un diámetro de 11, es decir, la distancia más grande entre dos vértices del grafo es de 11 aristas. Además, este subgrafo es un grafo de los llamados hamiltonianos, es decir, existe un camino (sucesión de vértices y aristas) que pasa por todos los vértices y en el que no se repite ningún vértice. Uno de esos caminos se muestra en la página A tour of Archimedes’ Stomachion, para quien esté interesado.
Y, para terminar, una escultura relacionada con los caminos hamiltonianos.

Bibliografía
1.- Reviel Netz, Fabio Acerbi, Nigel Wilson, Towards a Reconstruction of Archimedes’ Stomachion, SCIAMV 5, pp. 67-99, 2004.
2.- Grupo Alquerque de Sevilla (Juan Antonio Hans, José Muñoz, Antonio Fernández-Aliseda), Stomachion, el cuadrado de Arquímedes, SUMA, n. 50, pp. 79 – 84, 2005.
3.- Fan Chung, Ron Graham, A tour of Archimedes’ Stomachion
4.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, colección El mundo es matemático, RBA, 2015.
5.- Erica Klarreich, Glimpses of genius, Science News, n. 15, vol. 165, 2004.
6.- Wolfram Mathworld: Stomachion
7.- Tom Verhoeff, Koos Verhoeff, Three Mathematical Sculptures for the Mathematikon, Proceedings of Bridges 2016: Mathematics, Music, Art, Architecture, Education, Culture, pp. 105-110, 2016.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El de la RAE
dle.rae.es/?w=puzle
puzle
Del ingl. puzzle.
1. m. rompecabezas (‖ juego).
Jhon Edwin Chambi Arias
Buen material de trabajo para la matematica