Bohr había postulado que la cantidad mvr, que llamaremos «momento angular» [1] del electrón que orbita en el átomo de hidrógeno, donde r es el radio de la órbita del electrón, m es la masa de los electrones y v es su velocidad lineal [2], puede tener solo ciertos valores cuantizados. Estos valores cuantizados permiten definir los estados estacionarios.

La relación de de Broglie, λ = h/mv, esto es, el comportamiento ondulatorio de los electrones tiene una aplicación interesante y extremadamente simple que respalda este postulado [3] y ayuda a explicar la existencia de unos estados estacionarios y no otros. Veámoslo.

Bohr asumió que mvr solo puede tener los valores mvr = nh/2π [4], donde h es la constante de Planck y n un número natural que solo puede adoptar los valores n = 1, 2, 3, . . . .

Bien. Supongamos ahora que la onda asociada al electrón se extiende, de alguna forma, por la órbita circular de radio r, de tal forma que ocupa toda la órbita. Si esto es así la longitud de la circunferencia de la órbita, 2π tiene que ser igual a una longitud de onda o a un número entero n de longitudes de onda. En cualquier otro caso la onda se autoanula. Lo vemos en la figura: a la izquierda, encaja (fit), a la derecha no lo hace (no fit) y las ondas se anulan.

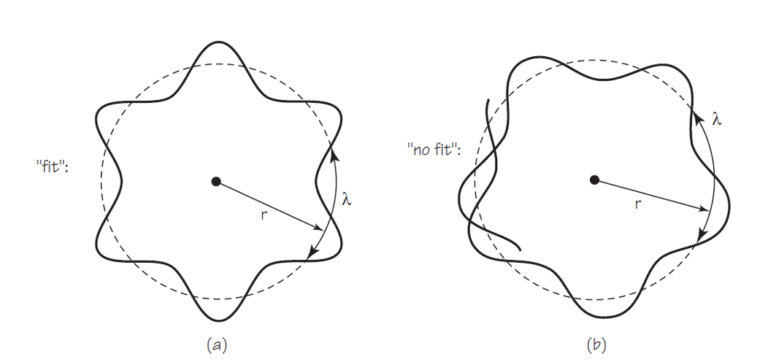
Si esto mismo lo reemplazamos por símbolos tenemos que 2πr, la longitud de la circunferencia, ha de ser igual a un número natural de longitudes de onda, nλ, o sea, 2πr = nλ. Por la relación de de Broglie sabemos que λ = h/mv, por tanto 2πr = nh/mv; que no es más que el postulado de Bohr escrito de otra manera ya que, simplemente reordenando obtenemos mvr = nh/2π.

La relación de Broglie para las ondas electrónicas unida a la idea de que los electrones tienen órbitas que permiten ondas estacionarias nos permite derivar la cuantización de las órbitas electrónicas que Bohr tuvo que asumir.

De lo que hemos visto resulta que uno se puede imaginar electrón que orbita en el átomo tanto como un corpúsculo que se mueve en una órbita con un cierto valor cuantizado del producto mvr como una onda tipo de Broglie estacionaria que ocupa una cierta región alrededor del núcleo.

Ya tenemos los mimbres básicos con los que construir la mecánica cuántica.

Notas:

[1] La definición estricta de momento angular puede llegar a complicarse mucho, conceptual y matemáticamente, sin embargo, y a los efectos que aquí nos ocupan, el producto del momento lineal en un instante (mv) por el radio (r) es más que suficiente y no del todo descabellado.

[2] Velocidad lineal es un componente de la velocidad total, ya que el electrón está en una órbita circular. Podemos interpretarla como la velocidad en un instante en la dirección de la tangente a la órbita en un punto.

[3] Recordemos que este postulado lo había introducido Bohr porque funcionaba pero sin saber por qué funcionaba.

[4] El que aparezca un 2π cuando estamos hablando de una órbita circular de longitud 2πr no debería extrañarnos.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance