Como dice el refranero popular No hay dos sin tres, por lo que la serie de entradas dedicadas al número tres, Las emocionantes aventuras del número tres (primera parte y segunda parte), no podía ser una dilogía, sino que tenía que consistir en una trilogía, como corresponde con el número del que estamos hablando.

En esta entrada vamos a hablar de la “regla del tres” en matemáticas, una regla sencilla, que nos han enseñado a todas las personas en la escuela y que tiene una larga historia, por su utilidad comercial y cotidiana. Veamos un ejemplo sencillo de la regla de tres.
Problema: El mes pasado hicimos una excursión al monte con un grupo de tiempo libre de 6 personas, en la cual se bebieron 15 litros de agua, ¿cuántos litros de agua se necesitarán para la siguiente excursión si en el grupo hay 16 personas?
Resolviendo este problema como yo recuerdo que me lo enseñaron en la escuela (yo soy de la generación de EGB) sería de la siguiente manera. En la imagen siguiente vemos el diagrama que acompaña a la resolución y mientras lo trazo voy diciendo, en alto o en mi mente, “6 es a 15, como 16 es a x” (en una columna, la primera, las cantidades correspondientes a personas y en la otra a litros de agua):

Una vez realizado el diagrama, la esencia de la regla de tres es que se tiene que el mismo resultado en las dos multiplicaciones en aspa.
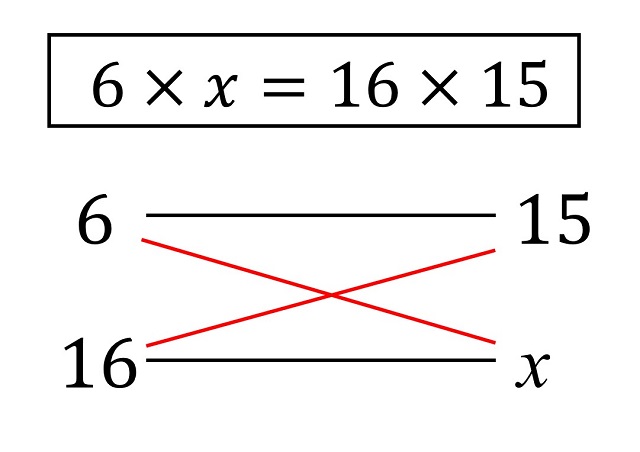
Por lo tanto, se puede despejar la x obteniendo:
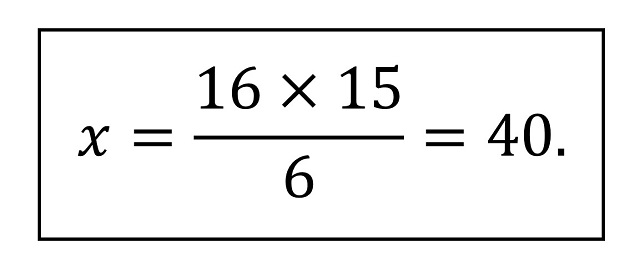
Luego la solución del problema es que se necesitarán unos 40 litros de agua.
La regla de tres es una cuestión de proporciones, como explicaremos más adelante, aunque muchas veces se ha enseñado desde un punto de vista práctico, explicando simplemente cuándo y cómo aplicarla. De hecho, esta es una regla con mucha historia, que aparece en muchos libros antiguos sobre resolución de problemas matemáticos o sobre cuestiones mercantiles, aunque sin dar explicaciones sobre la misma.
El origen de esta regla es muy antiguo. El capítulo 2 del texto chino anónimo del Jiuzhang suanshu (Nueve capítulos del arte matemático, escrito entre el 300 a.n.e. y el 200 n.e.) titulado Mijo y arroz sin cáscara, incluye 46 problemas que se resuelven con la regla de tres. Veamos por ejemplo el primer problema del capítulo Mijo y arroz sin cáscara. Al inicio del capítulo se dan algunas tasas de intercambio, así 50 unidades de mijo se intercambian por 30 unidades de mijo mal cascareado, que nos sirve para nuestro problema.
Problema (Jiuzhang suanshu): Tenemos un dou de mijo y queremos mijo mal cascareado, ¿qué cantidad deben darnos?
(Nota: el dou es una unidad de medida china cuya equivalencia es la siguiente, 1 dou es aproximadamente 2,95 kilogramos. Más aún, 1 dou son 10 sheng)
En este capítulo, Mijo y arroz sin cáscara, se da además la respuesta y la explicación a cada problema.
Respuesta: 6 sheng.
Método de resolución: multiplica uno por tres y divide por cinco.
Efectivamente, como el cambio del mijo es 50 unidades de mijo por 30 unidades de mijo mal cascareado, o lo que es lo mismo, 5 unidades de mijo por 3 de mijo cascareado, el diagrama de la regla de tres quedaría:
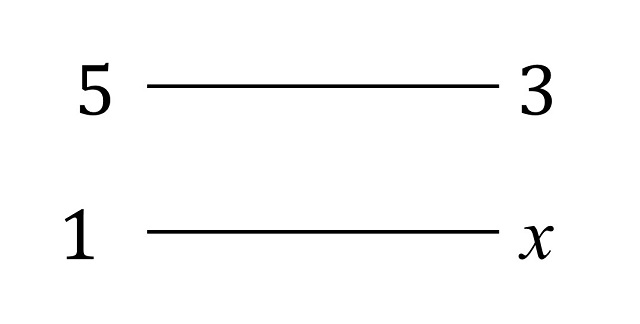
Luego la regla de tres nos dice que x = (1 x 3) / 5, como se escribe en el método de resolución “multiplica uno por tres y divide por cinco”. Luego la solución serían 3/5 dou, o lo que es lo mismo 6 sheng (puesto que 1 dou son 10 sheng).

Sin embargo, la regla del tres ya era conocida con anterioridad. Por ejemplo, muchos de los problemas que aparecen en el Papiro de Ahmes, o del Rhind, escrito en el siglo XVI a.n.e. a partir de textos anteriores (unos 300 años), implican el conocimiento de la regla de tres. Por ejemplo, el problema 72 pide calcular el número de hogazas de pan de “fuerza” 45 que son equivalentes a 100 hogazas de “fuerza” 10. Es decir,

Luego, la solución es 100 x 45 / 10 = 450 hogazas. Aunque para lo que nos ocupa no es necesario saber qué es la “fuerza”, vamos a explicarlo. La “fuerza” es el recíproco de la densidad en grano, que es el cociente entre el número de hogazas dividido por la cantidad de grano utilizado.

Sin embargo, un tratamiento más sistemático y extenso de la regla de tres se produce en la matemática de la India. La primera referencia escrita a la regla de tres en la India es el manuscrito Bakhshali, que podría ser el manuscrito más antiguo de la matemática india, puesto que está datado entre el año 224 y el 383. En el mismo se explica:
Si una cierta cantidad (llamada pramana) produce un cierto fruto (o phala), ¿qué fruto producirá otra cierta cantidad (llamada iccha)? La solución la proporciona el producto de phala por iccha, dividido por pramana.
Un ejemplo del manuscrito de aplicación de esta regla es el siguiente problema.
Problema: Un rey tiene dos pajes. Por sus servicios uno obtiene trece sextos de dinares por día y el otro tres medios. El primero debe al segundo diez dinares. Calcula y dime cuándo poseerán cantidades iguales y cuáles serán esas cantidades.
La respuesta a este problema es la siguiente. Como uno de los pajes gana 13/6 de dinares y el otro 3/2, entonces la diferencia entre las ganancias de cada uno es 2/3 de dinar al día. Los dos tendrán la misma cantidad cuando la diferencia entre las ganancias de los dos pajes sea el doble que la deuda (ya que si el primero ha ganado x y el segundo ha ganado y, tendrán la misma cantidad cuando x – 10 = y + 10, ya que el primero le debe al segundo 10 dinares). Como la diferencia de ganancia es 2/3 (pramana) de dinar por 1 (fruto) día, la diferencia de ganancia será de 20 (iccha) dinares, pasados
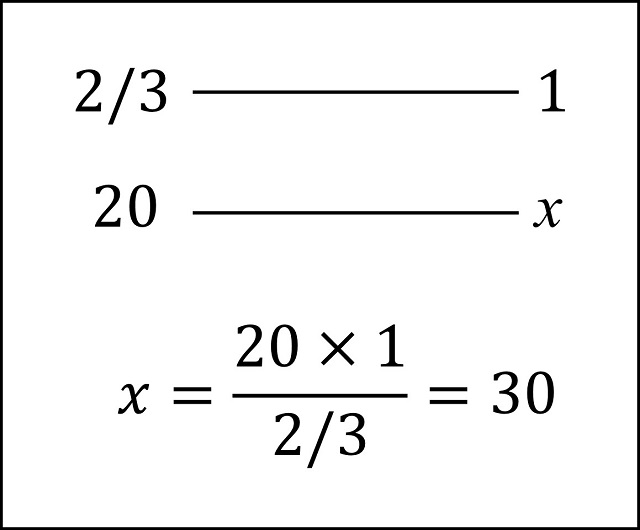
días.
Ahora para saber cuál es la cantidad de dinares que tendrán, cuando tengan la misma cantidad, podemos calcular cuánto gana el primer paje en esos 30 días. Como gana 13/6 (fruto) de dinares en 1 (pramana) día, entonces en 30 (iccha) días ganará lo siguiente.
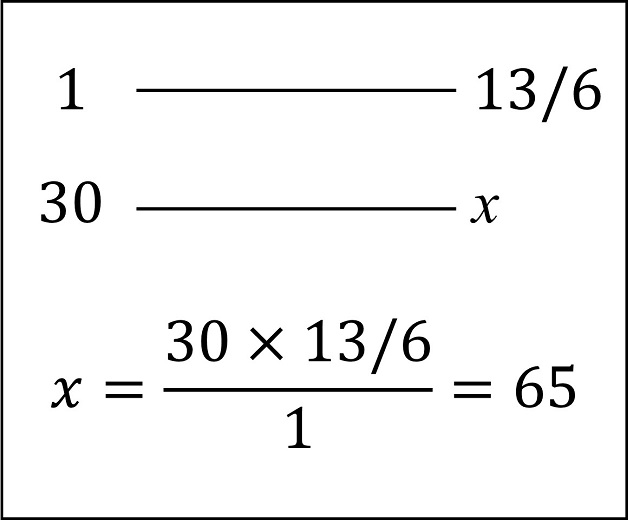
Es decir, en 30 días el primer paje ganará 65 dinares (y el segundo ganará 45 dinares), que tras saldar la deuda se quedará en 55 dinares, que es la cantidad de dinares que tendrán los dos trascurridos 30 días.
Entre los grandes matemáticos indios que estudiaron la regla de tres están Brahmagupta (590-670), Mahavira (siglo IX) y Bhaskara Acharya (1114-1185), quienes ya le daban el nombre de “regla de tres”. Brahmagupta en su texto Brāhmasphuṭasiddhānta –Doctrina correctamente establecida de Brahma– (628) escribe:
En la regla de tres, argumento, fruto y requisito son los nombres de los términos. El primero y el último son similares. Requisito multiplicado por fruto y dividido por argumento es el producto.
Si realizamos el diagrama y la regla asociados a la explicación de Brahmagupta tendríamos.
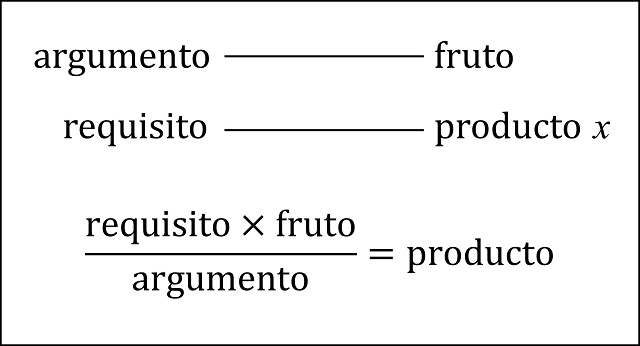
Mahavira en su libro Ganatasarasamgraha – Compendio de la esencia de las matemáticas–, del año 850 ofrece la misma descripción y términos que en el manuscrito Bakhshali.
El matemático y poeta indio Bhaskara Acharya en su libro en verso Lilavati contiene un capítulo sobre la regla de tres, otro dedicado a la regla de tres inversa y otro sobre la regla de tres compuesta directa. El Lilavati, como se explica en la edición en castellano que realizaron Ángel Requena y Jesús Malia para la colección biblioteca de estímulos matemáticos de la editorial SM y la Real Sociedad Matemática Española, “es un manual completo de matemática básica y media que abarca aritmética, álgebra, combinatoria, geometría y trigonometría”. Más aún, en este texto “un padre se dirige con ternura a su hija Lilavati para desentrañarle los secretos de la matemática a través de ejercicios en verso, lleno de evocadoras imágenes”.
Incluimos en esta entrada los primeros versos del capítulo 22, la regla de tres, de la preciosa edición de Ángel Requena y Jesús Malia.
{LXXIX}
Sabiendo tres cantidades obtenemos una cuarta.
Cantidad determinada, fruto de tal cantidad
y cantidad cuyo fruto queremos determinar
son el trío que principia y basta para operar.
El fruto final se obtiene de la siguiente manera:
opera, haz el producto de segunda por tercera
y, para concluir, divide después entre la primera.{LXXX}
Para obtener cantidad de la que sabes su fruto,
basta con multiplicar por la otra dicho fruto
para después dividir entre el término segundo.{LXXXI}
Por tres séptimos de niska llevo dos palas y media,
en especia, de azafrán.
Dime, hábil negociante, si te diera nueve niskas,
cuánto azafrán me darías.{LXXXII}
Si con ciento cuatro niskas se compran en el mercado
sesenta y tres olorosas palas de puro alcanfor,
dime, mi niña querida, cuánto me toca pagar
por doce palas y cuatro.

El nombre de regla de tres continuó con la difusión de la misma de los indios a los europeos, a través de los árabes, siguiendo el mismo camino que nuestro sistema de numeración posicional en base 10 y las cifras básicas del mismo (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), que se derivan de las indias (véase el libro Los secretos de la multiplicación, de los babilonios a los ordenadores).
Desde su origen, la regla de tres fue una herramienta fundamental para los comerciantes, que formaba parte de todos los tratados sobre “aritmética comercial”. Por este motivo, la regla de tres también se conoció con los nombres de “regla de los comerciantes” o “la llave de los comerciantes”.
El matemático galés Robert Recorde (1510-1558), quien introdujo el signo = en su libro de álgebra The Whetstone of Witte (1557), como explicamos en la entrada El origen de los signos matemáticos, escribió sobre la regla de tres: “la regla de las proporciones, la cual por su excelencia es conocida como regla de oro,…”. Y este nombre, la regla de oro, sería utilizado tanto por matemáticos, como por comerciantes.

Pero expliquemos que realmente la regla de tres es una regla que nos permite resolver cuestiones relacionadas con las proporciones. Es una aplicación de la multiplicación en cruz para las proporciones o fracciones.
Dadas dos fracciones, o proporciones, a / b y c / d, estas son iguales si se verifica la multiplicación en cruz, es decir, si al multiplicar los términos en cruz el resultado es el mismo, ad = bc (a multiplicado por d es igual a b multiplicado por c).
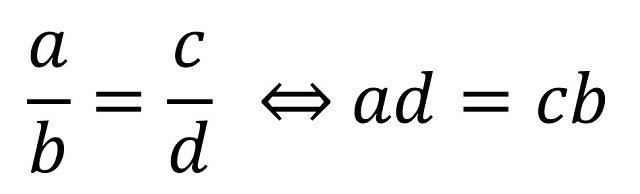
Demostrar que dos fracciones son iguales si, y sólo si, el resultado de la multiplicación en cruz es el mismo, es sencillo, basta con multiplicar a las dos fracciones por el producto de los dos denominadores, en este caso, por bd.
La regla de tres es realmente una relación de proporcionalidad. La idea que subyace cuando utilizamos la regla de tres es que las cantidades que aparecen en la misma están relacionadas por una regla de proporcionalidad. Así, tenemos que
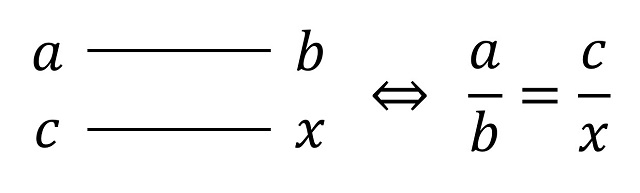
Luego, utilizando la multiplicación en cruz se tiene que ax = cb y despejando la incógnita se obtiene la regla de tres:
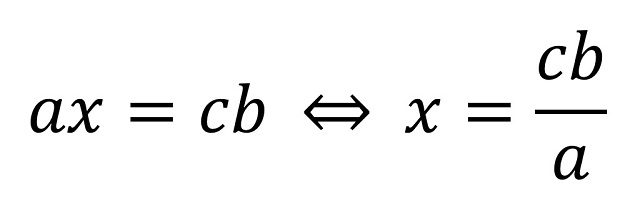
Volviendo al primer problema planteado en esta entrada –que decía así: “El mes pasado hicimos una excursión al monte con un grupo de tiempo libre de 9 personas, en la cual se bebieron 15 litros de agua, ¿cuántos litros de agua se necesitarán para la siguiente excursión si en el grupo hay 16 personas?”– estamos asumiendo que la proporción de agua bebida por cada persona es la misma, por lo tanto, 15 / 6 = x / 9. Lo mismo para el resto de problemas.

Y terminemos esta trilogía sobre el número tres con un refrán:
Los números nones son los mejores, y el número tres el mejor (de todos) es.
Bibliografía
1.- Josep Pla i Carrera, Liu Hui, Nueve capítulos de la matemática china, Nivola, 2009.
2.- George Gheverghese Joseph, La cresta del pavo real, las matemáticas y sus raíces no europeas, Pirámide, 1996.
3.- Carl B. Boyer, Historia de la matemática, Alianza Editorial, 1986.
4.- Ricardo Moreno Castillo, Aryabhata, Brahmagupta y Bhaskara, tres matemáticos de la India, Nivola, 2011.
5.- Bhaskara Acharya (versión adaptada y ampliada por Ángel Requena y Jesús Malia), Lilavati, Matemática en verso del siglo XII, SM-Real Sociedad Matemática Española, 2015.
6.- Raúl Ibáñez, Los secretos de la multiplicación, de los babilonios a los ordenadores, Catarata, 2019.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
Galois
En el primer problema el enunciado señala:
«El mes pasado hicimos una excursión al monte con un grupo de tiempo libre de 9 personas, en la cual se bebieron 15 litros de agua….» Nótese bien: nueve (9) personas.
Ahora bien, en los pasos de la resolución del problema, se utiliza el número 6 (seis) y no el 9.
César Tomé
Corregido, gracias.
Raúl
Gracias por la corrección:-)
La regla de tres, o las emocionantes aventuras …
[…] Como dice el refranero popular No hay dos sin tres, por lo que la serie de entradas dedicadas al número tres, Las emocionantes aventuras del número tres (primera parte y segunda parte), no podía ser una dilogía, sino que tenía que consistir en una trilogía, como corresponde con el número del que estamos hablando. En … […]
gemues
Siempre me pareció contraproducente el uso de la regla de tres, pues evita razonar en términos de proporcionalidad, algo que parece un mal endémico en la actualidad. Yo desterraría su uso para siempre, y lo recordaría incluso como un ejemplo de negligencia cognitiva.
Si cierto numero de personas necesitó cierto número de litros de agua durante cierta excursión, y consideramos razonable el consumo realizado de agua, de modo que creemos conveniente usar el mismo racionamiento en similares circunstancias, entonces solo tenemos que calcular la ración de agua, es decir, los litros por persona utilizados. Después, evidentemente, para cualquier número de personas, solo tenemos que multiplicar el número de personas por nuestra tasa por persona establecida.