Teoremas geométricos sin palabras: Herón
Esta tercera entrega de la serie estival de demostraciones sin palabras de interesantes y hermosos resultados geométricos, que habíamos iniciado con el clásico teorema de Viviani (en la entrada Teoremas geométricos sin palabras: Viviani) y que habíamos continuado con un teorema actual, el teorema de la circunferencia de Conway (en la entrada Teoremas geométricos sin palabras: Conway), la vamos a dedicar a la clásica fórmula de Herón para el área de un triángulo.
Pero antes de adentrarnos en la fórmula de Herón, vayamos a la resolución del problema que dejamos planteado en la anterior entrada.
Un cuadrado inscrito en un triángulo
En la anterior entrada dejamos propuesto el siguiente problema sobre cuadrados que aparece recogido en el artículo A Round-Up of Square Problemas (Una recopilación de problemas con cuadrados), de los matemáticos Duane Detemple y Sonia Harold, publicado en Mathematics Magazine en 1996.
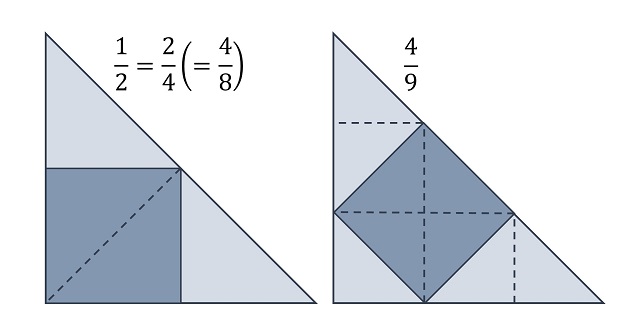
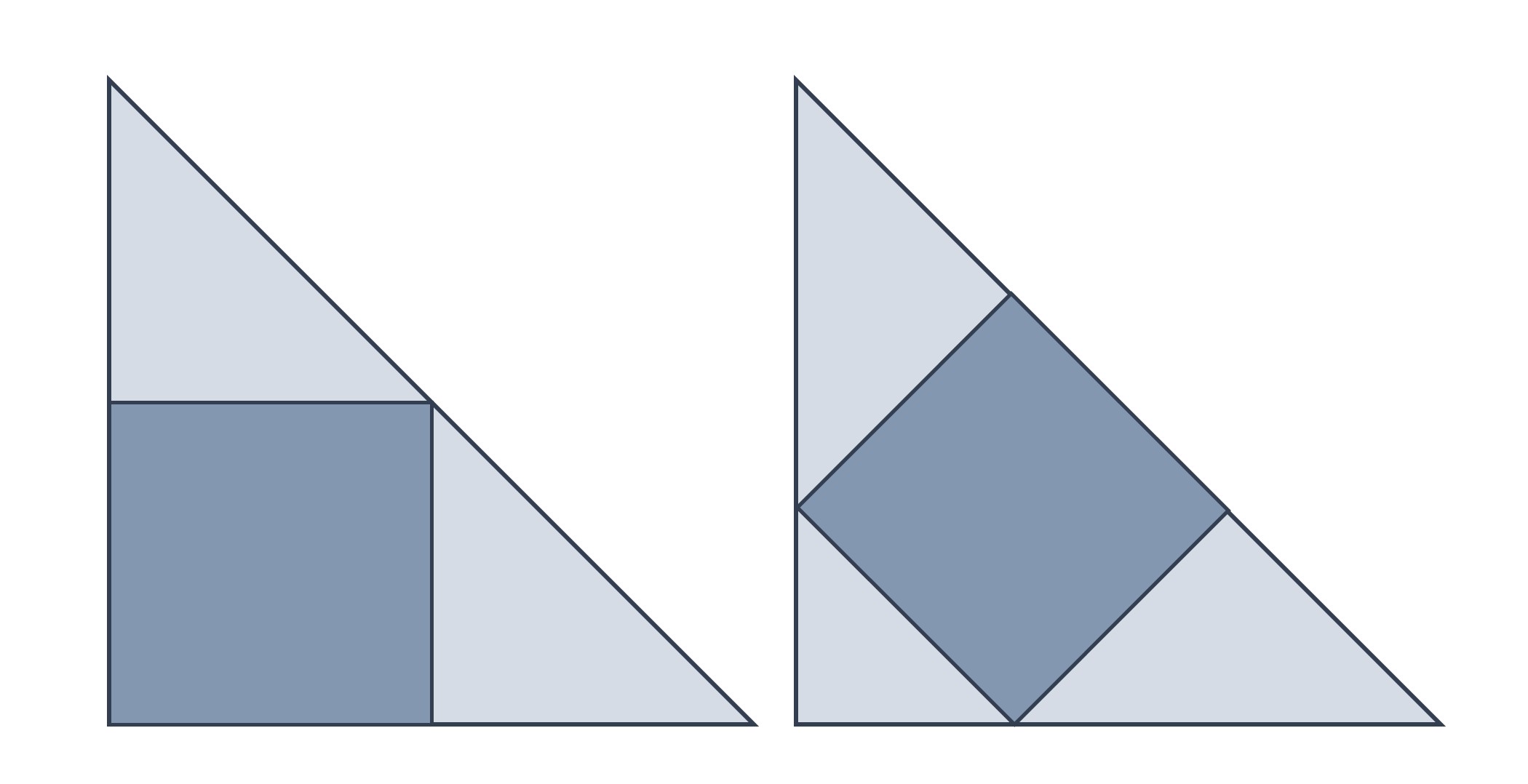
Problema (Un cuadrado inscrito en un triángulo rectángulo isósceles): Estos dos cuadrados han sido inscritos en un mismo triángulo rectángulo isósceles, pero de dos formas distintas, como se muestra en la imagen. ¿Cuál de los dos cuadrados tiene una mayor superficie?
La solución a este problema es sencilla, la mayor superficie corresponde al cuadrado de la izquierda, y se puede realizar con una sencilla imagen.
La fórmula clásica del área de un triángulo
Todas las personas hemos estudiado en la escuela la sencilla fórmula para calcular el área de un triángulo, que no es otra que la mitad de la base por la altura del triángulo: Área = (base x altura) / 2.
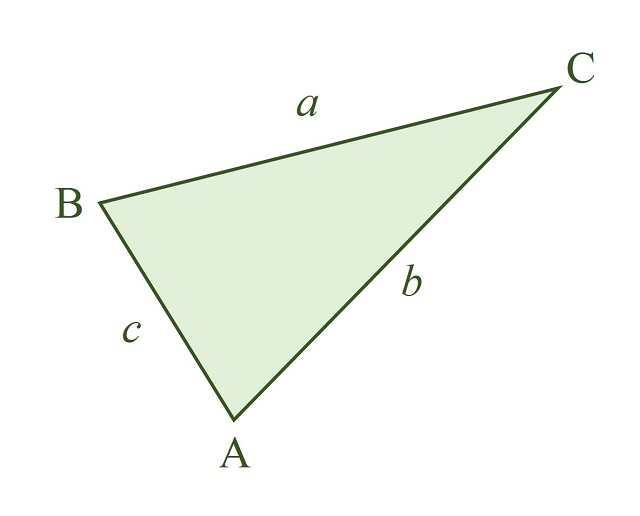
A pesar de la sencillez de esta fórmula, podemos plantear algunas objeciones a la misma. Dado un triángulo ABC, con lados a, b y c, como el que aparece en la siguiente imagen, la primera objeción es que la información que solemos tener de este polígono es la longitud de sus lados, es decir, a, b y c, luego no es posible calcular el área directamente con esa información.
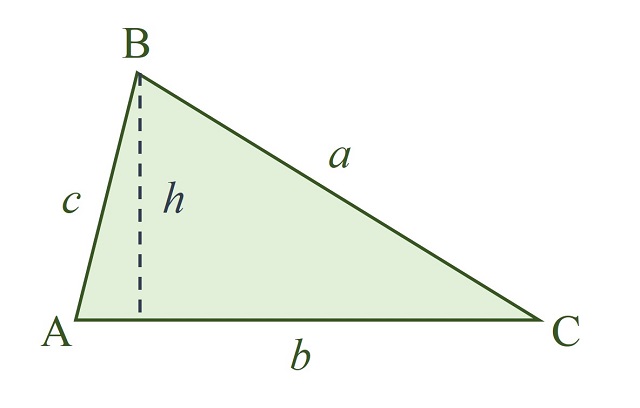
Además, dada la mencionada fórmula (base por altura dividido por dos) disponemos de tres opciones distintas para la base –obviamente, cada uno de los tres lados a, b o c– y, por lo tanto, también para la correspondiente altura. Por ejemplo, si en el anterior triángulo ABC tomamos como base el lado b, tendremos la altura h que aparece en la siguiente imagen.
Pero no disponemos, a priori, de la información del valor de la altura h, por lo tanto, debemos de calcularlo (en la educación primaria normalmente nos daban el valor de la altura o era un triángulo rectángulo de manera que la base y la altura eran los catetos del mismo). ¿Cómo calcular la altura h, a partir de los valores de los lados a, b y c? Este es el típico problema de aplicación del teorema de Pitágoras en educación secundaria (aunque para valores concretos de los lados). Veamos cómo se solucionaría de forma genérica.
Llamamos u a una parte de la base determinada por la intersección de esta con la altura, de forma que la otra será b – u, como en la siguiente imagen.
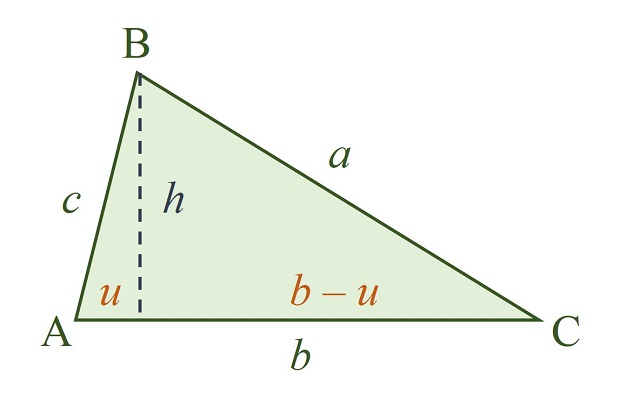
Entonces, se aplicaría el teorema de Pitágoras a los dos triángulos rectángulos determinados por la altura (h, u, c) y (h, b – u, a), obteniéndose las expresiones:
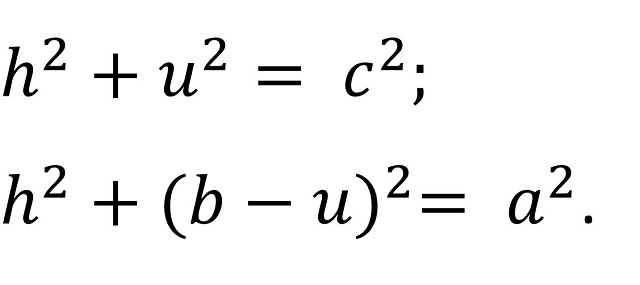
Restando ambas expresiones se tiene que a2 – c2 = b2 – 2bu y despejando u podemos obtener su valor en función de los lados a, b y c:
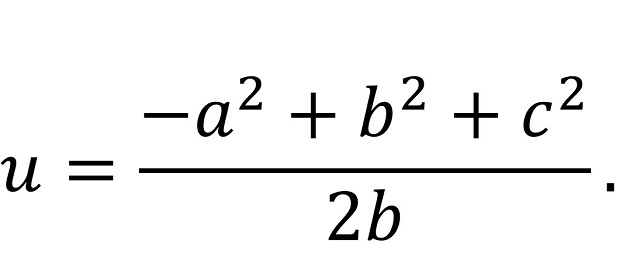
Una vez obtenido el valor de u podemos calcular h2 con la primera de las fórmulas anteriores, h2 = c2 – u2, obteniéndose la siguiente expresión (con un pequeño cálculo intermedio, que obviamos para no abusar de las fórmulas):
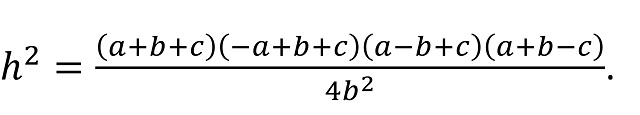
De esta forma hemos obtenido una expresión general para la altura h, si la base es b, en función de los lados a, b y c, haciendo uso del teorema de Pitágoras. Ahora, si llamamos s al semi-perímetro, es decir, s = (a + b + c) / 2, e introducimos el valor de h en la fórmula del área del triángulo, base b por altura h dividido por 2, se obtiene la expresión:
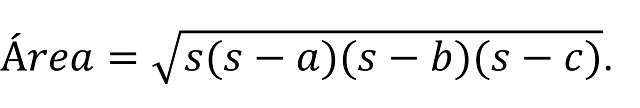
De esta forma, hemos obtenido una expresión para el área del triángulo en función, directamente, de los lados del mismo, a, b y c. Esta es la conocida como fórmula de Herón para el área del triángulo.
Así, si consideramos un triángulo de lados 13, 14 y 15, tendríamos que el semi-perímetro sería s = 21 y el área s, por la fórmula de Herón, sería la raíz cuadrada del producto de 21, 8, 7 y 6, luego de 7.056, que es 84.
La fórmula de Herón (sin palabras)
La anterior fórmula del área del triángulo debe su nombre al matemático e ingeniero griego Herón de Alejandría (aprox. 10 – 70 a.n.e.), que la incluyó en su libro Metrica (alrededor de 60 a.n.e., aunque este manuscrito estuvo perdido hasta 1896). Esta fórmula podría ser conocida ya por el matemático e ingeniero griego Arquímedes de Siracusa (aprox. 287 – 212 a.n.e.), según aparece recogido en las obras del científico persa Al-Biruni (973 – después de 1.050).
Existen diferentes demostraciones de la fórmula de Herón, además de la mostrada en esta entrada haciendo uso del teorema de Pitágoras, pero nosotros, como corresponde a esta serie veraniega, vamos a mostrar la demostración que el matemático Roger B. Nelsen publicó en la revista College Mathematics Journal, en 2001, utilizando los argumentos de las demostraciones sin palabras.
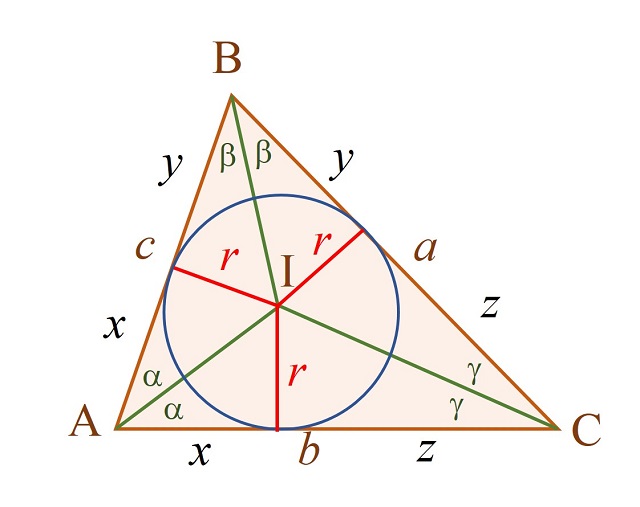
Dado un triángulo ABC, las rectas que bisecan los ángulos en los vértices A, B y C (llamadas bisectrices) se intersecan en un punto P, que no es otro que el incentro I del triángulo ABC (el centro de la circunferencia inscrita en el triángulo ABC).
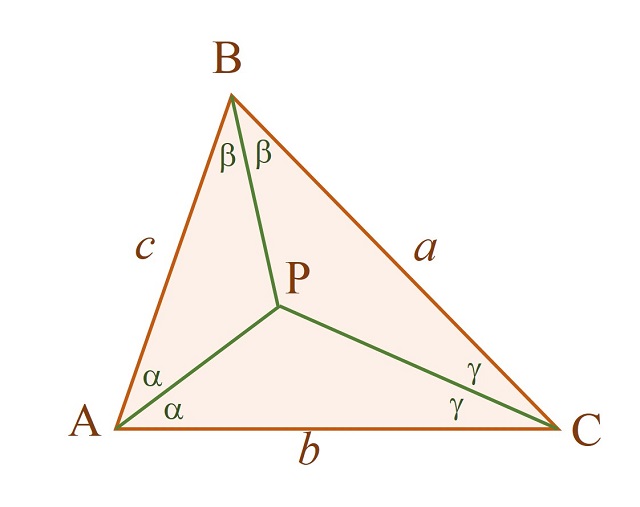
Efectivamente, si trazamos desde el punto P los tres segmentos perpendiculares a los lados a, b y c (en rojo en la siguiente imagen) se generan tres pares de triángulos semejantes (dos triángulos semejantes en cada vértice del triángulo ABC), de manera que esos tres segmentos tienen la misma longitud r, el radio de la circunferencia inscrita en el triángulo ABC. Por lo tanto, efectivamente P es el incentro I del triángulo.
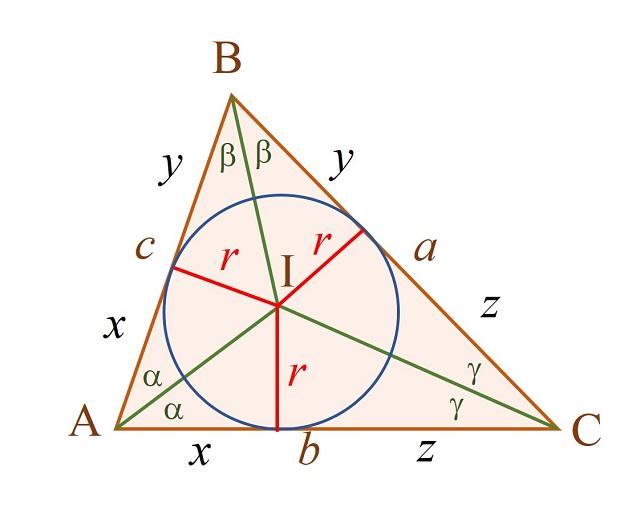
Además, llamando x, y y z como en la anterior imagen, tenemos que los lados son a = y + z, b = x + z y c = x + y, que el semi-perímetro es s = x + y + z y que entonces x = s – a, y = s – b y z = s – c.
Para demostrar la fórmula de Herón vamos a demostrar primero (sin palabras) dos pequeños resultados técnicos previos (lo que en matemáticas llamamos “lemas”).
Lema 1: El área del triángulo ABC es igual al producto del semiperímetro s y el radio r de la circunferencia inscrita en el mismo (de centro I).
La demostración de este resultado es el siguiente diagrama, que consiste en una reordenación de los tres pares de triángulos semejantes de la imagen anterior.
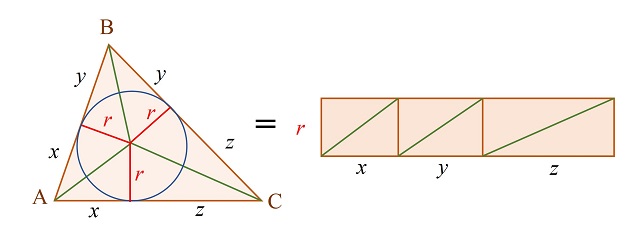
El siguiente lema es un resultado un poco técnico sobre trigonometría (podéis saltároslo si os parece muy técnico) que describe una relación entre tres ángulos alpha α, beta β y gamma γ cuya suma sea un ángulo recto, es decir, 90 grados. Por lo tanto, luego podremos aplicar este lema a los tres ángulos alpha α, beta β y gamma γ, que son la mitad de los ángulos en los vértices A, B y C del triángulo ABC, como hemos mostrado en una imagen anterior, y que suman, por tanto, 90 grados.
Lema 2: Si alpha α, beta β y gamma γ son tres ángulos positivos cuya suma es 90 grados, entonces
Para demostrar (sin palabras) este segundo lema técnico vamos a construir el siguiente rectángulo, jugando un poco con la trigonometría, y a igualar el valor de la longitud de los dos lados paralelos, de la izquierda y la derecha, del rectángulo.
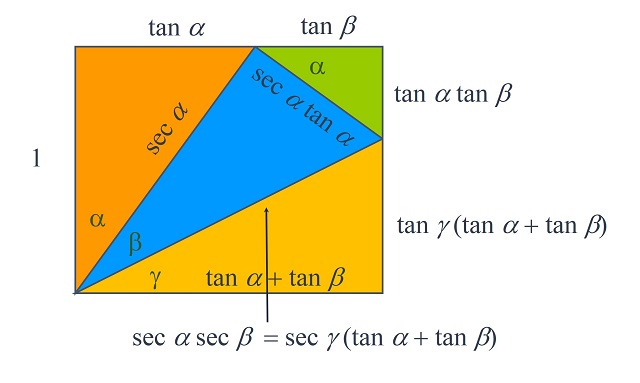
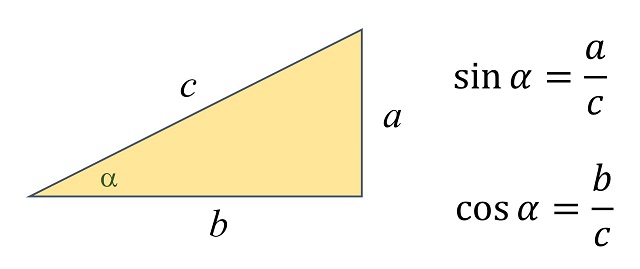
Nota: Podemos recordar algunas de las definiciones básicas de la trigonometría. Dado un ángulo alpha α se considera el triángulo rectángulo tal que alpha α es el ángulo entre uno de sus catetos y la hipotenusa, como en la siguiente imagen, entonces se definen el seno y el coseno como el cociente entre uno de los catetos y la hipotenusa, para el seno el cateto opuesto al ángulo y para el coseno el otro cateto.
Además, se definen la tangente, la secante y la cosecante del ángulo como
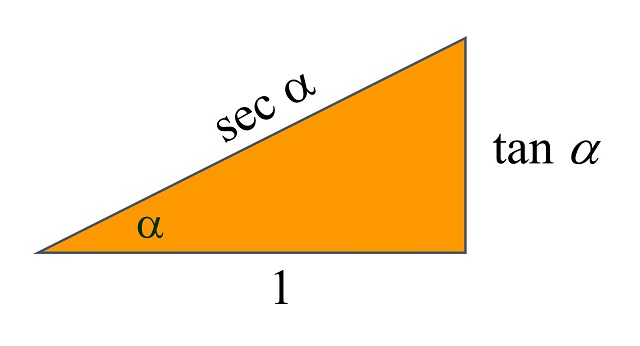
Por este motivo, si el triángulo anterior (de la definición del seno y el coseno), lo redimensionamos dividiendo sus lados por b, de forma que ese cateto tendrá una longitud de 1, queda el siguiente triángulo
que es uno de los que aparecen en el rectángulo de la prueba visual del lema 2.
Si ahora se aplica el lema 2 al diagrama anterior en el que se descomponía el triángulo ABC en tres pares de pequeños triángulos rectángulos de ángulos alpha α, beta β y gamma γ, que recordamos en la siguiente imagen,
entonces se tiene que:
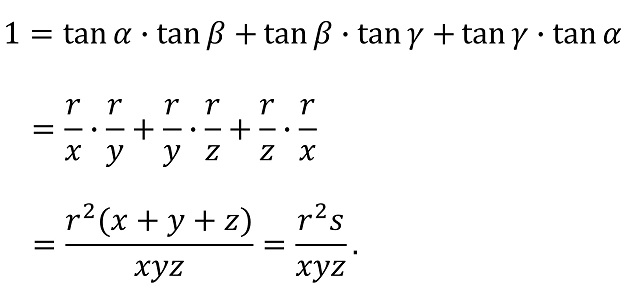
Ahora, teniendo en cuenta el lema 1 se tiene
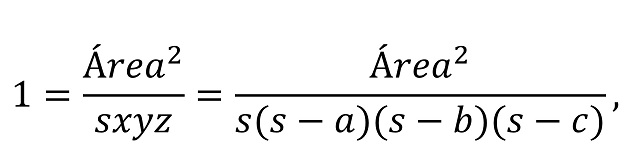
que demuestra la fórmula de Herón.
Cuadrados inscrito y circunscrito a una circunferencia
Una vez más, como viene siendo habitual en esta serie estival, vamos a terminar esta entrada con un sencillo problema que puede ser resuelto con un razonamiento visual.
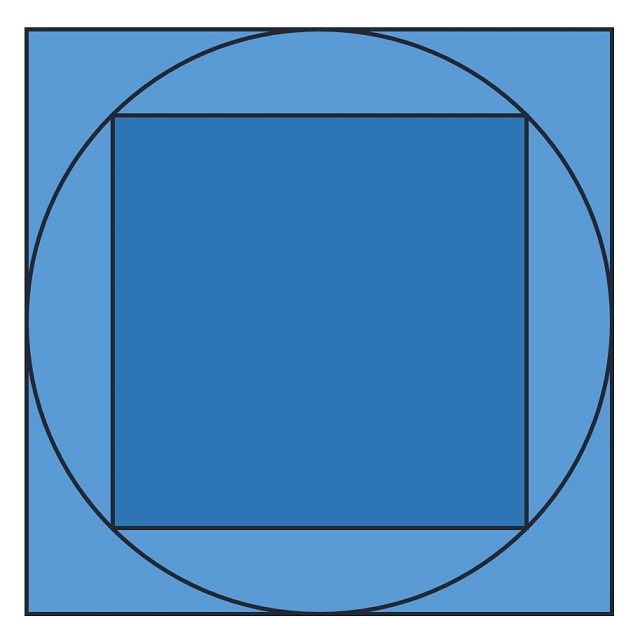
Problema (Cuadrados inscrito y circunscrito a una circunferencia): ¿Cuál es la proporción de las áreas de los cuadrados inscrito y circunscrito a una misma circunferencia?
Bibliografía:
1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.
2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.
3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.
4.- Wolfram MathWorld: Heron’s formula
5.- Roger B. Nelsen, Heron’s Formula via Proofs Without Words, College Mathematics Journal, September, 2001.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
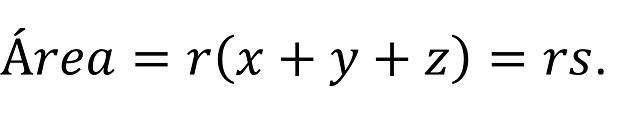
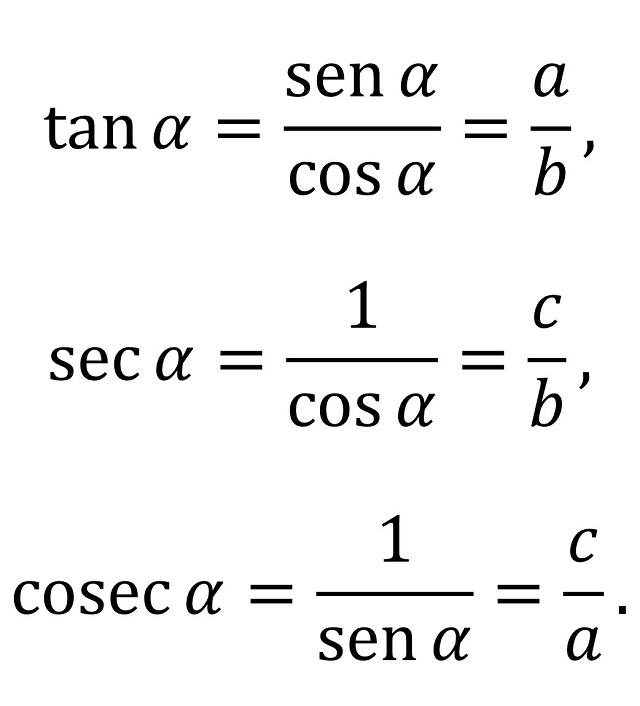
Teoremas geométricos sin palabras: Her&o…
[…] La fórmula de Herón permite calcular el área del triángulo en función, directamente, de los lados del mismo Y se demuestra sin palabras. […]