Con esta entrada damos por terminada la serie estival de demostraciones sin palabras de interesantes y hermosos resultados geométricos, que hemos dedicado al clásico teorema de Viviani (en la entrada Teoremas geométricos sin palabras: Viviani ), al moderno, con sabor a clásico, teorema de la circunferencia de Conway (en la entrada Teoremas geométricos sin palabras: Conway) y a la fórmula de Herón para el área de un triángulo (Teoremas geométricos sin palabras: Herón), y la vamos a dedicar, como en el caso de las anteriores entradas, a un resultado geométrico sobre triángulos, pero en este caso se trata de un sencillo resultado que no tiene nombre (aunque podríamos denominarlo “teorema de Snover”, como explicaremos más adelante), pero que me parece curioso, interesante y con una demostración sin palabras simple y elegante.

Pero antes, vayamos a la resolución del problema sobre cuadrados inscritos y circunscritos a una circunferencia que dejamos planteado en la anterior entrada.

Cuadrados inscrito y circunscrito a una circunferencia

El problema que planteamos en la anterior entrada para ser resuelto con un razonamiento visual era el siguiente.

Problema (Cuadrados inscrito y circunscrito a una circunferencia): ¿Cuál es la proporción de las áreas de los cuadrados inscrito y circunscrito a una misma circunferencia?

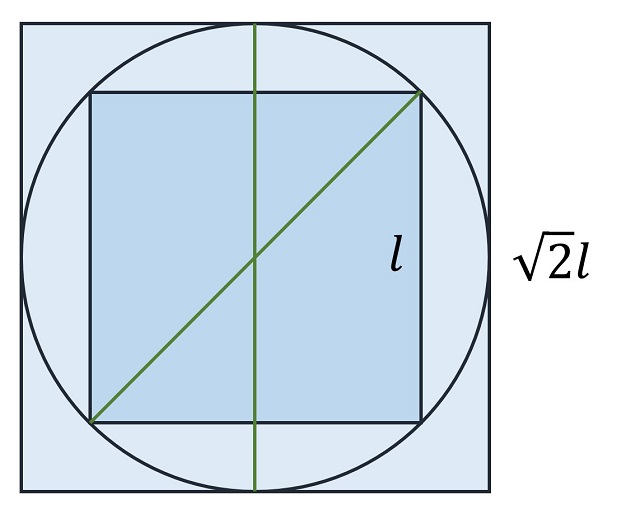
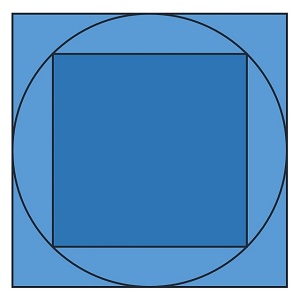
La solución es bastante simple, el cuadrado inscrito tiene la mitad de área que el cuadrado circunscrito, o al revés, el área del cuadrado circunscrito es el doble que la del inscrito. Como se muestra en la siguiente imagen, la diagonal del cuadrado inscrito a la circunferencia es igual al lado del cuadrado circunscrito, lo cual es suficiente para obtener la solución al problema.

Un pequeño teorema sobre áreas de triángulos

Descubrí este resultado en el segundo de los libros de la serie de demostraciones sin palabras del matemático Roger B. Nelsen: Proofs Without Words II: More Exercises in Visual Thinking (MAA, 2001). Nelsen lo presentó bajo el título “Cuatro triángulos con la misma área” y mencionó al matemático Steven L. Snover como su autor (a través de una comunicación privada), motivo por el que hemos aprovechado para denominarle, en esta entrada, teorema de Snover.

Veamos en qué consiste este resultado geométrico que bien podía haber estado incluido en la gran obra de la matemática griega, y universal, Los Elementos, del matemático griego Euclides de Alejandría (aprox. 325 – 265 a.n.e.). Se parte de un triángulo cualquiera y se trazan tres cuadrados, cada uno de ellos de lado igual a uno de los lados del triángulo y apoyado en el mismo, como se muestra en la siguiente imagen.

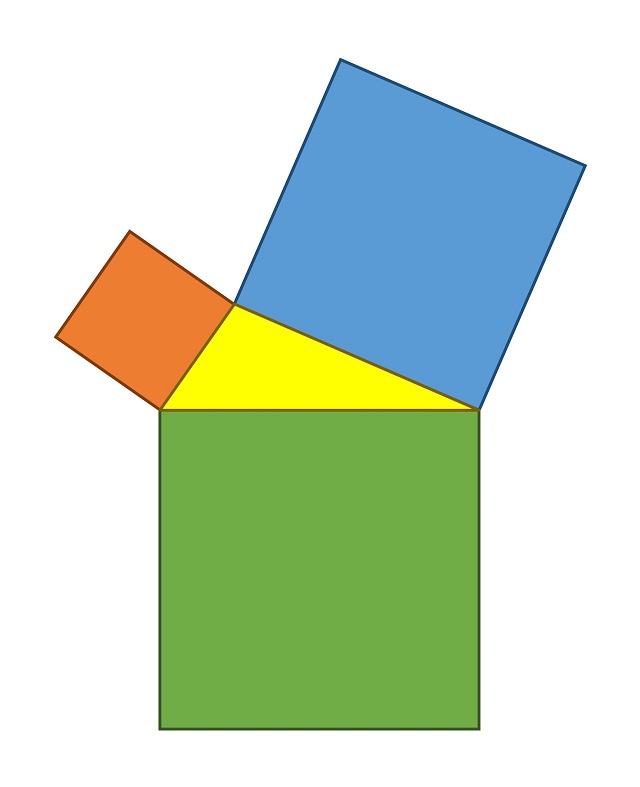
Esta primera construcción nos recuerda a la construcción del diagrama básico del teorema de Pitágoras (véanse las entradas Pitágoras sin palabras y Paseando entre árboles de Pitágoras), pero ahora partimos de un triángulo cualquiera, no necesariamente un triángulo rectángulo.

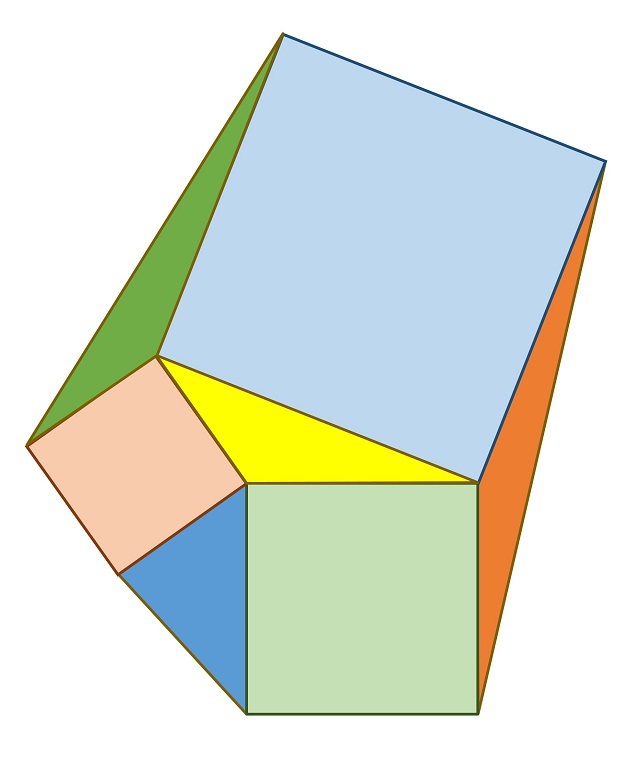
El siguiente paso consiste en trazar los tres triángulos formados por un vértice del triángulo y los vértices externos de los cuadrados construidos apoyados en dicho vértice, como se muestra en la imagen: triángulos azul, verde y marrón.

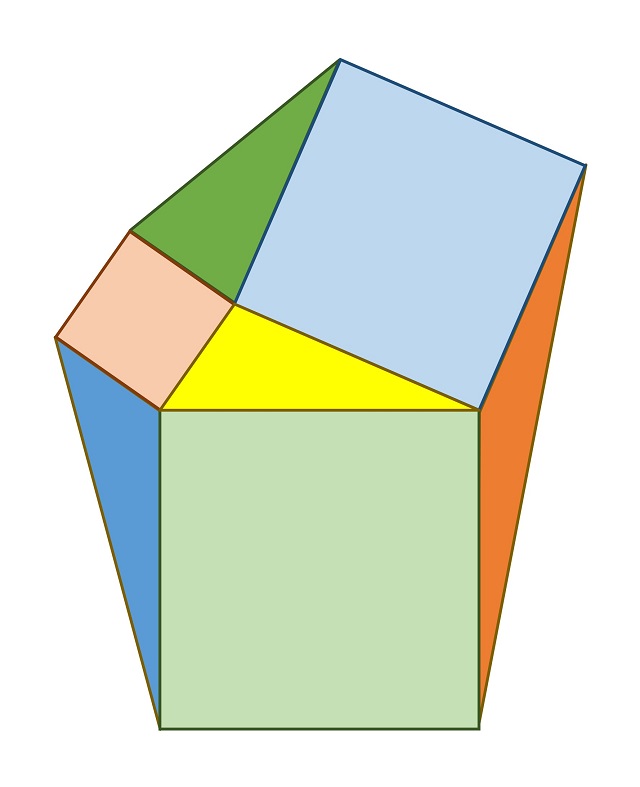
El resultado geométrico consiste en que esos tres nuevos triángulos que se han construido (azul, verde y marrón) tienen la misma área que el triángulo original (amarillo).

Teorema (de Snover): Dado un triángulo cualquiera, para cada lado del mismo se construye un cuadrado de lado igual al lado del triángulo y apoyado en el mismo. Entonces, los tres triángulos formados, cada uno de ellos, por un vértice del triángulo y los vértices externos de los cuadrados construidos apoyados en dicho vértice, tienen la misma área que el triángulo original.

El resultado es verdadero independientemente de la forma del triángulo, ya sea equilátero (todos los lados iguales), isósceles (dos lados iguales y uno diferente), escaleno (los tres lados diferentes), acutángulo (todos los ángulos agudos, es decir, entre 0 y 90 grados), rectángulo (con un ángulo de 90 grados) u obtusángulo (con un ángulo obtuso, es decir, mayor de 90 grados). Da igual como sea el triángulo original, los tres nuevos triángulos tendrán su misma área.

Demostración sin palabras

La demostración es muy sencilla y se basa en que cada uno de esos tres triángulos tiene la misma base y la misma altura (alguna de las tres opciones que existen para base y altura del triángulo) que el triángulo original, luego como el área de un triángulo es igual a la base por la altura dividido por dos, se concluye el resultado.

Veamos el argumento visual para el primer triángulo dibujado en esta entrada.

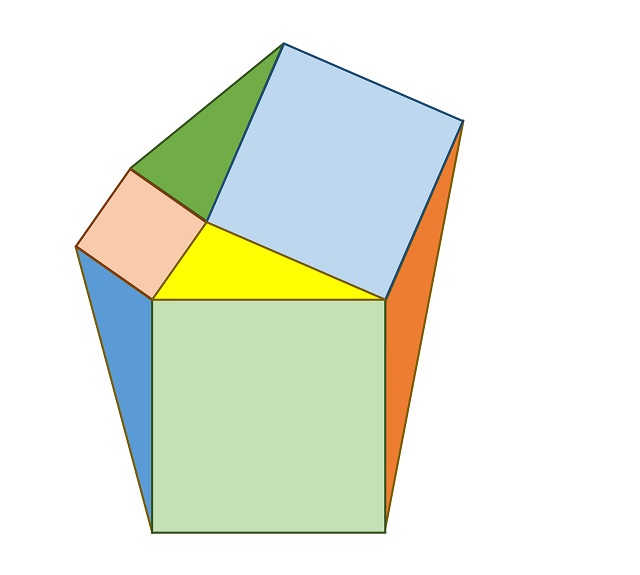
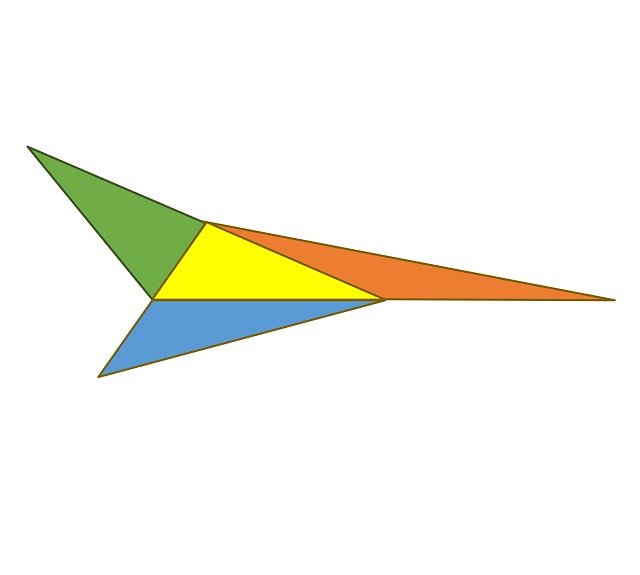
Espero que hayáis disfrutado de esta miniserie de cuatro entradas dedicadas a demostraciones sin palabras de interesantes y hermosos resultados geométricos sobre triángulos. Seguro que en el futuro volveremos con más hermosas demostraciones sin palabras.

Bibliografía:

1.- Roger B. Nelsen, Proofs without Words: Exercises in Visual Thinking, Mathematical Association of America, 1997.

2.- Roger B. Nelsen, Proofs Without Words II: More Exercises in Visual Thinking, Mathematical Association of America, 2001.

3.- Claudi Alsina y Roger B. Nelsen, Charming Proofs, A Journey Into Elegant Mathematics, Mathematical Association of America, 2010.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica